自動控制原理是研究控制系統行為和性能的科學。穩定性是控制系統的一個重要性能指標,它描述了系統在受到擾動后能否恢復到平衡狀態的能力。
1. 穩定性的定義
穩定性是指系統在受到初始條件或外部擾動后,其狀態能否在有限時間內恢復到平衡狀態或穩定在某個范圍內。穩定性分為以下幾種類型:
- BIBO(有界輸入有界輸出)穩定性 :對于任何有界輸入,系統的輸出也是有界的。
- L2穩定性 :系統的能量(輸出的平方和)是有限的。
- L∞穩定性 :系統的最大輸出是有界的。
2. 線性時不變系統(LTI系統)的穩定性
對于線性時不變系統,穩定性的判斷主要依賴于系統的特征值或極點。
2.1 極點配置
線性時不變系統的傳遞函數可以表示為:
[ H(s) = frac{b(s)}{a(s)} = frac{b_0 + b_1s + cdots + b_ms^m}{a_0 + a_1s + cdots + a_ns^n} ]
其中,( b(s) ) 和 ( a(s) ) 是系統的分子和分母多項式。系統的穩定性可以通過分析 ( a(s) ) 的根(即極點)來判斷。
- 穩定條件 :所有極點的實部都必須是負的。
- 臨界穩定 :至少有一個極點的實部為零。
- 不穩定 :至少有一個極點的實部為正。
2.2 勞斯-赫爾維茨判據
勞斯-赫爾維茨判據是一種基于極點的穩定性分析方法。對于一個實系數多項式,如果其所有根的實部都是負的,則稱該多項式是赫爾維茨穩定的。
3. 非線性系統的穩定性
非線性系統的穩定性分析比線性系統更為復雜,通常需要使用一些近似方法或數值方法。
3.1 李雅普諾夫方法
李雅普諾夫方法是判斷非線性系統穩定性的一種常用方法。基本思想是構造一個李雅普諾夫函數 ( V(x) ),該函數沿著系統的運動是非減少的,即:
[ dot{V}(x) leq 0 ]
如果 ( V(x) ) 在平衡點附近滿足以下條件,則系統在該平衡點是穩定的:
- ( V(x) ) 在平衡點處為零。
- ( V(x) ) 在平衡點附近是正定的。
- ( dot{V}(x) ) 在平衡點附近是非正定的。
3.2 相平面分析
對于二階非線性系統,可以通過相平面分析來判斷系統的穩定性。在相平面上,系統的軌跡可以表示為一組微分方程:
[ dot{x} = f(x, y) ]
[ dot{y} = g(x, y) ]
通過分析相平面上的流線和等勢線,可以判斷系統的穩定性。
4. 穩定性的數值分析方法
對于復雜的系統,數值分析方法是一種有效的穩定性分析手段。
4.1 時域仿真
通過數值積分求解系統的微分方程,觀察系統在長時間內的響應。如果系統能夠在有限時間內恢復到平衡狀態,那么系統是穩定的。
4.2 頻域分析
通過計算系統的頻率響應,可以分析系統的穩定性。例如,奈奎斯特判據和伯德圖可以用來判斷閉環系統的穩定性。
5. 穩定性的工程應用
在工程實踐中,穩定性分析對于控制系統的設計至關重要。
5.1 控制器設計
在控制器設計過程中,需要確保閉環系統的穩定性。常用的控制策略如PID控制、狀態反饋控制和最優控制等,都需要考慮系統的穩定性。
5.2 系統優化
穩定性分析可以用于系統優化,通過調整系統參數或結構來提高系統的穩定性。
-
控制系統
+關注
關注
41文章
6604瀏覽量
110576 -
參數
+關注
關注
11文章
1829瀏覽量
32195 -
自動控制
+關注
關注
10文章
714瀏覽量
44155 -
函數
+關注
關注
3文章
4327瀏覽量
62573
發布評論請先 登錄
相關推薦
控制上是怎么描述穩定性?如何判斷一個系統是否穩定呢?
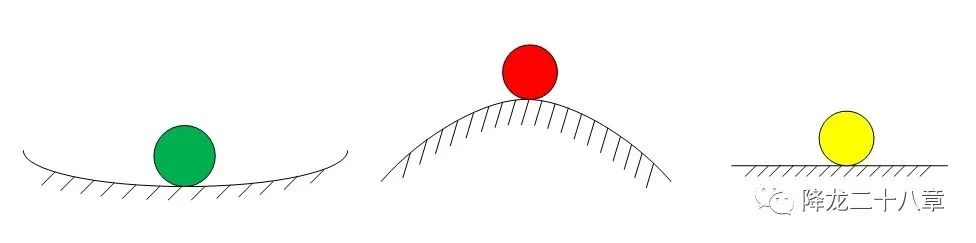
運放穩定性的判斷原理的補償原理?
環路增益的穩定性
怎樣去調試電源控制環穩定性呢
PLC控制系統的穩定性分析與提高
直接能量平衡法協調控制系統穩定性對策研究
跟隨伺服控制系統的輸入狀態穩定性




 自動控制原理怎么判斷系統的穩定性
自動控制原理怎么判斷系統的穩定性










評論