邏輯函數(shù)的化簡是數(shù)字電路設(shè)計(jì)中的重要步驟,它有助于減少電路中的門數(shù)量,提高電路的性能和可靠性。邏輯函數(shù)的化簡方法主要可以分為兩大類:
- 公式化簡法 :
- 代數(shù)法 :利用布爾代數(shù)的公理、定理和規(guī)則(如德摩根定律、分配律、結(jié)合律、吸收律、互補(bǔ)律等)對(duì)邏輯函數(shù)進(jìn)行變換,從而得到最簡形式。這種方法通常需要對(duì)邏輯表達(dá)式進(jìn)行多次變換,直到無法再進(jìn)一步簡化為止。
- 卡諾圖化簡法 :卡諾圖(Karnaugh Map, K-Map)是一種圖形化的化簡方法。通過將邏輯函數(shù)的真值表映射到二維的方格圖上,并利用相鄰方格間的邏輯關(guān)系來合并最小項(xiàng)或最大項(xiàng),從而得到最簡的邏輯表達(dá)式。卡諾圖化簡法特別適用于變量數(shù)較少(一般不超過6個(gè))的邏輯函數(shù)。
- 機(jī)器化簡法 :
- 隨著計(jì)算機(jī)技術(shù)的發(fā)展,出現(xiàn)了許多基于計(jì)算機(jī)的邏輯函數(shù)化簡工具和方法。這些工具和方法通常利用高效的算法(如奎因-麥克拉斯基方法(Quine-McCluskey method, QM方法)、埃斯普勒斯基方法(Espresso method)等)來自動(dòng)完成邏輯函數(shù)的化簡過程。機(jī)器化簡法能夠處理更復(fù)雜的邏輯函數(shù),并且能夠在較短時(shí)間內(nèi)得到最優(yōu)或接近最優(yōu)的化簡結(jié)果。
需要注意的是,雖然機(jī)器化簡法在處理復(fù)雜邏輯函數(shù)時(shí)具有顯著優(yōu)勢,但在某些情況下(如需要深入理解邏輯函數(shù)的結(jié)構(gòu)或進(jìn)行手動(dòng)設(shè)計(jì)時(shí)),公式化簡法仍然是不可或缺的工具。
綜上所述,邏輯函數(shù)的化簡方法主要分為公式化簡法和機(jī)器化簡法兩大類。其中,公式化簡法又包括代數(shù)法和卡諾圖化簡法兩種具體方法。
-
邏輯函數(shù)
+關(guān)注
關(guān)注
0文章
23瀏覽量
9504 -
數(shù)字電路
+關(guān)注
關(guān)注
193文章
1605瀏覽量
80580 -
機(jī)器
+關(guān)注
關(guān)注
0文章
780瀏覽量
40711
發(fā)布評(píng)論請先 登錄
相關(guān)推薦
邏輯代數(shù)和函數(shù)化簡
第四講 邏輯函數(shù)的公式化簡法
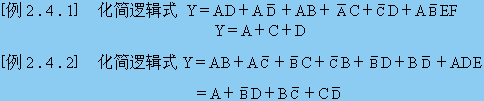
第五講 邏輯函數(shù)的卡諾圖化簡法
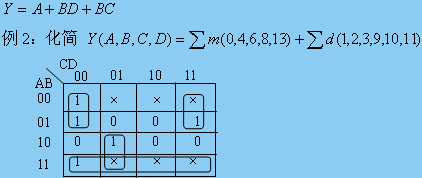
邏輯函數(shù)的卡諾圖化簡法
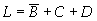
邏輯函數(shù)的公式化簡法
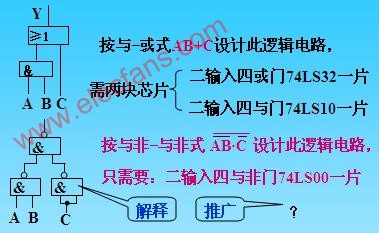
采用表格法化簡邏輯函數(shù)技術(shù)
邏輯代數(shù)的化簡算法
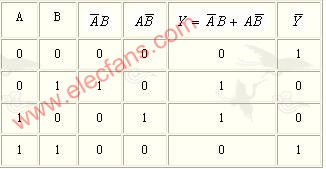




 邏輯函數(shù)的化簡方法有哪兩種
邏輯函數(shù)的化簡方法有哪兩種










評(píng)論