補償器是使控制系統在動態運行中快速穩定的電子濾波器。在絕大多數的研究中，補償器是置于運算放大器（op amp） 周圍的一個有源電路，其特點被認為是完美的。如果這種方法可用于低帶寬系統，如今的轉換器即使輸出電容小，交叉頻率超過100千赫就能確保足夠快的瞬態響應以限制輸出壓降。在這些應用中，考慮一個完美的運算放大器的計算不再工作，并最終誘導嚴重的增益和相位失真。通過揭示開環增益和所選運放的兩個低頻和高頻磁點如何影響整體響應，可以選擇合適的元件，避免影響交叉時所需的增益和相位特性。這第一部分將重點關注開環增益的影響，有意忽略了低頻和高頻磁點。第二部分將探討這些額外的極點的影響，并顯示如果沒有適當選擇，它們如何削弱最終結果。

不同類別的補償器

補償器的作用是形成一個給定電路的頻率響應-例如降壓轉換器-以便一旦閉環，控制系統表現出所需的交叉頻率 f_c 和適當的相位 / 增益裕度。補償器通過提供在 f_c 的一些中期波段的增益或衰減強行形成 0 dB 交叉點。相位裕度 j_m 由補償器在 f_c 表現出的相位提升（phase boost）量調節。最后，增益裕度取決于交叉后補償器調降增益的能力。

有不同類型的補償器，其在開關轉換器中通常命名為 type 1 、type 2 和 type 3 。所有三個型號在原點都有一個極點以提供最大可用準靜態增益（S = 0），提供一個精確的輸出變量。type-1 補償器是個簡單的積分電路，完全不提供相位提升。type 2 基于 type 1，和增加了一個極 / 零對以提供最大90°的相位提升。最后，type-3 電路提供另一個極零對，可提升相位達180°。圖1顯示了三種補償器的頻率響應（幅度和相位）及各自的傳遞函數表達式。更多關于這些電路的信息請查閱[ 1 ]。

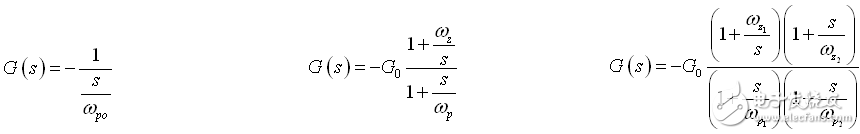
圖1：您選擇的補償器與您想要的相位提升量有關

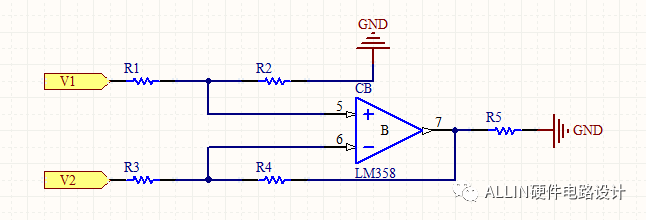
Type-2 補償器常見于電流模式電源，其最大相位提升90°，可提供大量補償。圖2所示為它用于運算放大器周圍。您可觀察一個檢測所監測變量（V_out，本例子中為輸出電壓）的電阻分壓器和幾個形成濾波器的無源元件。為確定該轉換器的傳遞函數，我們將首先考慮運放的開環增益 A_OL ，并看看它如何影響最終的表達式。該電路的傳遞函數 G 是聯系勵磁信號 V_out 到輸出響應 V_FB 的數學關系。

圖2：在該補償器中，我們考慮運放具有有限開環增益，但我們尚不考慮其內部極點。

簡介快速分析技術

有許多方法來確定該濾波器的動態響應。本文將使用快速分析電路技術（FACTs），如[ 2 ]和[ 3 ] 所描述的。這些 FACTs 的基本原理是確定在兩個不同條件下的電路時間常數：激勵信號消失（V_out降至0 V）時和響應清零（V_FB= 0）時。通過使用這種技術，您將了解確定一個特定的傳遞函數有多快速和直觀。

如參考文獻所示，一個具有非零準靜態增益的第一階系統的傳遞函數可表示為：

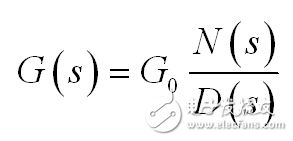
（1）

首項 G₀ 是 S = 0 時系統表現出的增益。視情況而定，該項帶有單位。在這里，因為我們談論的增益是[V] / [V] ，沒有單位，G 是無量綱的。分子的 N(s) 控制傳遞函數的零點。在數學上，零點是個特定的點 s_z，其響應為空。從理論上講，考慮到激勵信號覆蓋整個 s 面（諧波模式下不僅在垂直軸），當輸入信號調到零角頻率 s_z ，零點表現為輸出響應的調零。電路中一些特定阻抗組合阻擋了信號傳播，響應為0 V，盡管存在激勵源。零點是分子的根。請注意這是個方便的數學抽象，大大有助于通過檢測找到零點，無需寫一連串代數。關于這種方法的更多細節請查閱[ 4 ]。

分母 D（s ） 由電路自然時間常數構成。通過設置激勵信號為0和確定這種結構中所考慮的電容或電感“所示”的阻抗而得出這些時間常數 t= RC 或 t= L / R 。通過“觀察”，我的意思是您想象把歐姆表置于暫時移除的電容或電感器，并讀取它顯示的電阻。這其實是個相當簡單的練習。看看圖3無源電路，您看到一個注入源-激勵-偏置網絡的左側。輸入信號通過網格和節點傳播以形成觀察到的電阻 R₃ 的響應。

The response：響應

The excitation：勵磁

圖3：確定電路的時間常數需要將勵磁設置為0，并觀察從電路中暫時移除的能量存儲元件所提供的電阻。

為確定本例電路的時間常數，我們將勵磁設置為0（一個 0V 電壓源換為短路和 0A 電流源開路），拆下電容器。然后，我們連接（在我們頭腦中）一個歐姆表，以確定由電容器端提供的電阻。圖4引導您進行這些步驟。

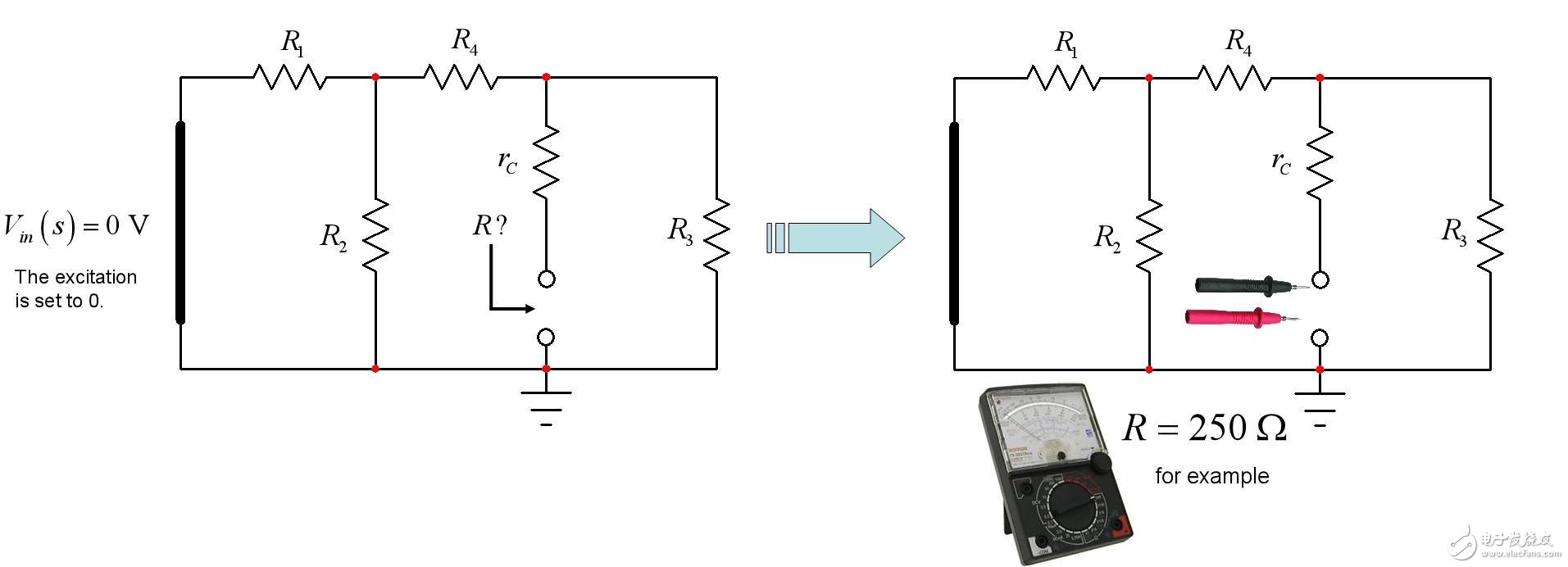
The excitation is set to 0：勵磁設為0

For example：例如

圖4：在 0V 源換為短路后，您確定電容器端的電阻。

如果您按圖4進行練習，您“看到”R₁ 與 R₂ 并聯后與與 R₄ 串聯，所有這些與 R₃ 并聯后與 r_C 串聯。該電路的時間常數只通過 R 和 C₁ 即可計算得出：

（2）

我們可證明，一個第一階系統的極點是其時間常數的倒數。因此：

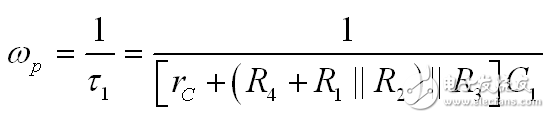
（3）

現在，s= 0 時這個電路的準靜態增益是多少？在直流條件下，電感器短路，電容器開路。把這個概念應用于圖3的電路，繪制如圖5所示。您想象在 R₄ 前切斷連接，會看到一個含 R₁ 和 R₂ 的電阻分壓器。R₂ 上的戴維寧(Thévenin)電壓為：

（4）

輸出電阻 R_th 是 R₁ 與 R₂ 并聯的值。因此完整的傳遞函數涉及到與 R_th 串聯的 R₄ 和加載的 R₃ 所構成的電阻分壓器。r_C 是斷開的，由于電容 C₁ 在這直流分析中被移除。因此可寫：

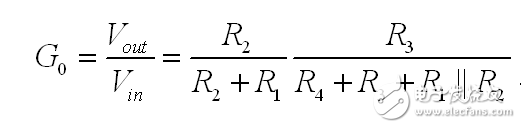
（5）

您斷開直流電路中的電容器，計算這個簡單的電阻排列的傳遞函數。

基本就是這些了，我們正錯過零點。我們如何知道是否到了零點？嗯，這是個有用的技巧：在你的頭腦中考慮圖3的電路，短路電容 C₁ 。現在，假設您激勵具有短路電容器的電路。您能夠基于示波器觀察 V_out 的響應嗎？當然， r_C 短路 R₃ ，盡管振幅可能低，輸入信號仍會傳播并有響應。如果這個練習的答案是“是的，盡管 C₁ 短路，但仍然有響應”那么有與 C₁ 有關的零點。如果您處理含一個電感 L₁ 的電路，然后進行同樣的練習，但采用電感開路。如果在這模式仍有響應，那么有與 L₁ 有關的零點。

我們在序言中說，零點通過阻斷激勵信號的傳播而在電路中表現出來，并產生輸出為空。如果我們考慮一個變形電路–其中 C₁ 被

1/sC₁ 代替–如圖6所示，當勵磁偏移網絡，有什么特定的條件意味著響應為空？有一個空響應只意味在 R₃ 循環的電流為0。如果電阻沒有電流，沒有電壓施加和 V_out 是 0 V，這不是短路，而是虛擬的接地。

圖6：在這變形電路中，當 r_C 和 C₁ 串聯轉化為短路，響應消失。

如果 R₃ 沒有電流，那么 r_C 和 1/sC₁ 串聯創建一個轉換的短路：

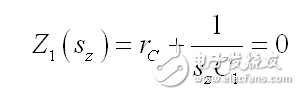
（6）

根 s_z 是我們需要的零點位置：

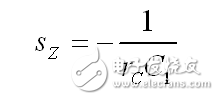
（7）

從而有：

（8）

現在，我們可以組合所有這些結果，形成以圖3電路為特征的最終的傳遞函數：

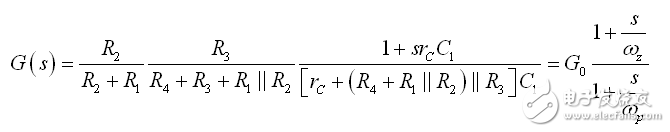
（9）

這就是所謂的低熵表達式，您可立即識別增益、極點和零點。高熵表達式將在考慮阻抗分壓器時通過施加大規模外力到原來的電路來獲得，例如：

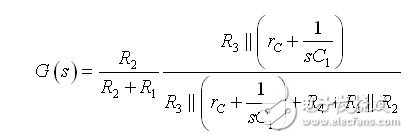
（10）

不只您可能在推導表達式時犯錯誤--我也會！但是將結果格式化到像（9）這樣需要更多的精力。此外，請注意，在寫（9）時我們沒有寫一行代數。如果我們后來發現一個錯誤，那么易于回到一個單獨的圖紙并單獨修復它。（9）的校正將是容易的。現在嘗試在（10）進行相同的修正，您可能會從頭開始。您檢查一下，在 Mathcad? 表繪制的表達式（9）和（10）的頻率響應是相同的，如圖7所示。

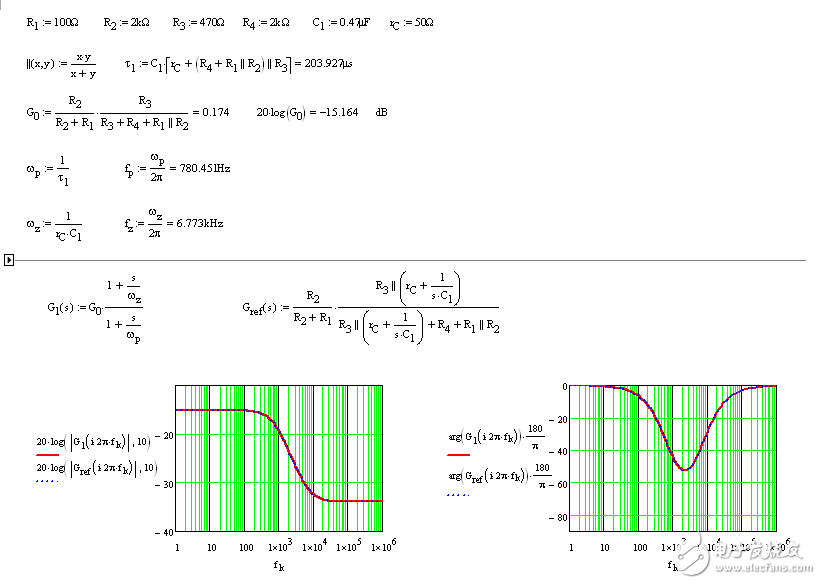
圖7：快速 Mathcad? 告訴您用 FACTs 推導出的表達式是否與由原表達式返回的響應相匹配。

FACTs 的簡介意在說明在簡單和更復雜的電路上使用它們是多么輕松和高效。通過將一個復雜的體系結構分解為簡單的單獨的電路，您可以很快地編寫傳遞函數，有時只通過檢查，正如我們所做的那樣。既然我們已介紹了工具，讓我們把它應用到我們的 type 2 補償器。

FACTs 應用于 Type-2 補償器

為高效地運用 FACTs 到圖2的電路，我們開始于計算儲能元件： C₁ 和 C₂ 。考慮到它們的獨立狀態可變—如它們不是串聯的或并行的--這是個二階系統。考慮非零準靜態增益，這樣的系統可以表示為以下形式：

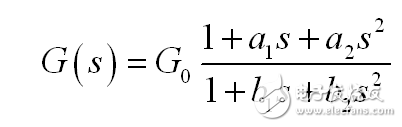
（11）

對于二階系統，我們可以證明分母遵循下列公式：

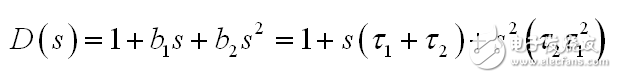
（12）

系數 s 僅僅是確定零點激勵的時間常數之和。S2 系數稍微復雜，因為它引入了一個新的符號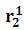：。此符號意味著您“看到”的 C₂ 終端的阻抗，而 C₁ 由短路取代。乍一看有點難以理解，但沒有不可逾越的，我們用幾句話解釋就會明白。

按照求解圖3電路的途徑，我們可研究 s= 0 的系統，如圖8所示。在分析的過程中，V_ref 是個完美的源及其動態響應為0（忽略我們應用的調制，它的電壓是固定的）。因此，它自然不存在于小信號電路，在交流分析中采用短路的形式。

圖8：在直流條件下，斷開所有的電容：運算放大器運行于開環配置。

運算放大器提供的電壓相當于開環增益 A_OL 的 e 倍。反相引腳的電壓與低邊阻抗 R_lower 有關，在這種情況下，e 是個非零的值：

（13）

在這個電路中，我們有兩個電容，因此有兩個單獨的時間常數。為確定與 C₂ 有關的第一個時間常數，我們將激勵信號設為0，我們從看到的 C₂ 確定阻抗，C2 連接端子，而 C1 從電路中移除。草圖如圖9。

Set excitation to 0：將勵磁設為0

圖9：與電容 C₂ 有關的第一個時間常數：在其端子間您看到的阻抗是多少？

如果在前面的例子檢查得很好，電壓控制源的存在-運算放大器-用這簡單的方法是行不通的。為確定由 C₂ 端提供的阻抗，我們可連接測試生成器 I_T ，我們將決定其兩端的電壓 V_T 。然后 V_T / I_T 會給我們提供想要的阻抗。涉及電流源的草圖如圖10所示.。您可寫的第一個簡單的等式與 e 有關。運算放大器的輸入引腳之間的電壓是施加在并聯的 R₁ 和 R_lower 的電壓的負值：

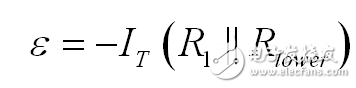
（14）

：您安裝一個測試發生器以確定 C₂ 兩端的阻抗。

運算放大器的輸出為開環增益 A_OL 的 e 倍。因此：

（15）

將(14)代入(15)得出：

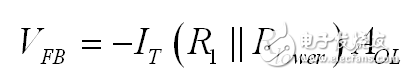
（16）

V_T 是電流源的電壓。在其左側端有負的 e 而右側偏移 V_FB ：

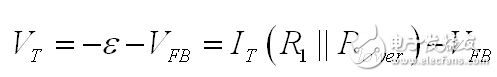
（17）

如果我們從（17）提取 V_FB ，結合（16）的結果，我們有：

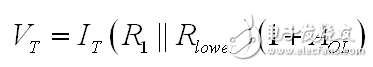
（18）

我們的阻抗是簡單的：

（19）

因此第一個時間常數 t₂ 表示為：

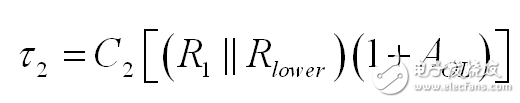
（20）

第二個時間常數與 C₁ 有關，需要更新的原理圖，如圖11所示。我們沒有安裝電流發生器，因為結果很明顯：C₁ 兩端的電阻就是已經確定的 C₂ 的電阻與 R₂ 串聯：

：立即確定第二個時間常數，因為它是驅動 C₂ 的電阻與 R₂ 串聯。

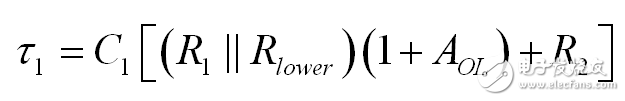
（21）

我們有兩個時間常數，我們可以進行第二階項。我們說，我們需要評估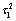

，其中 C₂ 被短路，而我們從 C₁ 的終端看電阻。圖12顯示了新的草圖。既然我們在與 R₂ 有關的回路中有弗蘭克短路，那么電阻 R 就是 R₂：

（22）

因此，如果我們根據（12）組合時間常數，我們得出分母D(s)：

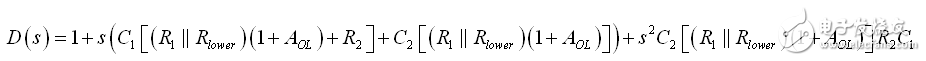
（23）

圖12：高頻系數采用了神秘的符號但最終并不復雜：短路的C₂和確定C₁端電阻。

這二階形式可以重新排列，假設質量因子Q遠遠小于1。在這種情況下，那么兩個極點完全分離：一個控制低頻，而第二個位于頻譜的上部。由（12）我們可以證明，兩個極點定義為：

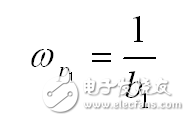
（24）

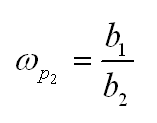
（25）

如果我們將這些定義應用到（23），簡化和重新排列，我們得到：

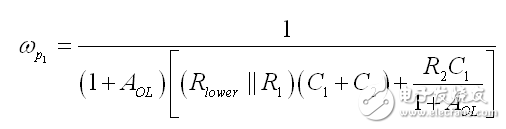
（26）

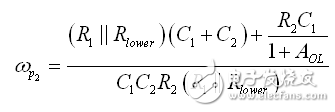
（27）

既然我們有分母，我們這個電路有零點嗎？我們可以運用之前展示的技巧：如果我們想象短路，C₁或C₂然后C₁和C₂，這三個配置有響應嗎？如果C₁短路，我們有一個含R₂和其他電阻的簡單的逆變器：有個與C₁有關的零點。如果C₂短路，則運算放大器為0：C₂沒有零點。如果兩個電容器都短路，當然，沒有響應。為確定零位置，圖13中的什么可以防止勵磁的傳播，使響應為空？如果C₁和R₂提供的阻抗變為轉化的短路，那么響應消失：

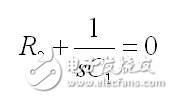
（28）

然后

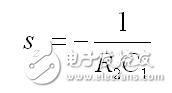
（29）

圖13：如果由R₂與C₁串聯的阻抗成為轉化的短路，那后響應為空：這就是零點如何產生的。

其中給出了零點位于：

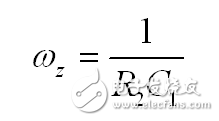
（30）

我們現在有最終的傳遞函數

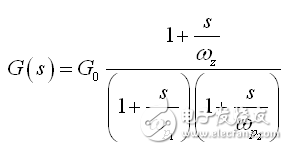
（31）

及

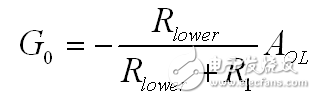
（32）

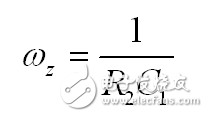
（33）

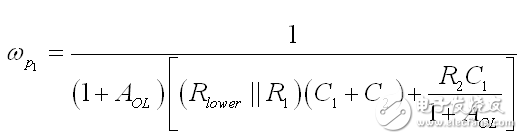
（34）

（35）

比較電路之間的響應

現在比較由 type-2 電路(其中我們考慮開環增益)帶來的動態響應是有意義的，下面給出了 type 2 完美的傳遞函數：

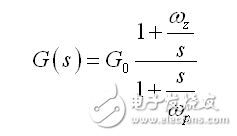
（36）

其中

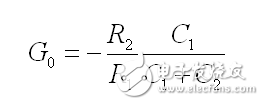
（37）

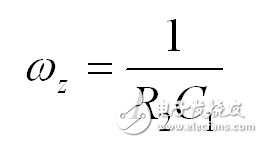
（38）

（39）

舉例說明，我們比較理想的運放和開環增益 50 dB 的運放（例如 TL431）當補償器必須達到以下目標：f_c= 10 kHz 和在這個頻率 20 dB 的增益補償，相位提升必須是65°。R₁和R_lower計算用于 12V 輸出和 2.5 V 參考電壓。（31）和（36）的兩個動態響應如圖14所示。交叉增益和相位升壓的偏差可以忽略不計。然而，在120赫茲頻率時（31）的增益為35 dB，（36）則為45dB。最后，有限的A_OL選項的準靜態增益僅36.4 dB（?66），而無限時則為完美的運算放大器。這些數字的影響是什么？在兩倍的電源頻率的增益不足將影響控制系統的能力，排斥整流紋波。輸出變量可能會受到這個組件的影響，特別是在電壓模式控制下。此外，控制變量可能有顯著的靜態誤差，如果植入增益低。如果您現在選擇具有更高A_OL的運算放大器，例如 80dB，偏差消失，兩曲線相互非常接近，如圖15所示。

圖14：type 2 的波特圖中，我們考慮開環增益A_OL和低邊電阻R_lower的作用與原完美的等式并不會相差太多。

圖15：當開環增益A_OL增加，兩條曲線很好地疊加。準靜態增益提高到66.3 dB，對比于采用50dB A_OL增益時的36 dB 。

總結

這第一部分證明了在采用非理想運算放大器的補償器中開環增益的影響。當運算放大器不再被認為是完美的，您可以看到在動態響應的低頻范圍內弱開環增益的影響，和評估這種情況帶來的性能下降。在這第一部分中，我們只考慮開環增益的影響。在第二部分中，我們將復雜化分析，添加兩個低頻和高頻極點，集成電路設計人員自然將其置于一個運算放大器中以確保其穩定性。

參考文獻

1.C. Basso, “ Designing Control Loops for Linear and Switching Converters – A Tutorial Guide”, Artech House 2012, ISBN 978-1-60807-557-7

2.C. Basso, “Linear Circuit Transfer Functions – An Introduction to Fast Analytical Techniques”, Wiley 2016, ISBN 978-1-119-23637-5

3.V. Vorpérian, “Fast Analytical Techniques for Electrical and Electronic Circuits”, Cambridge University Press 2002, ISBN 978-0-521-624428

4.C. Basso, “Fast Analytical Techniques at Work with Small-Signal Modeling”, APEC Professional Seminar, Long Beach (CA), 2016, http://cbasso.pagesperso-orange.fr/Spice.htm

↓↓↓閱讀原文，查看更多！