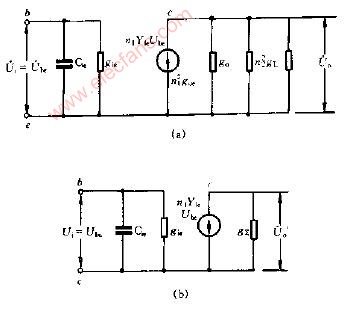
等效電路:

L:變壓器漏感及元器件引線電感等雜散電感之和。
D、Cd:整流二極管,Cd為D的結電容。
Q、Coss:開關MOSFET,Coss為MOSFET的結電容。
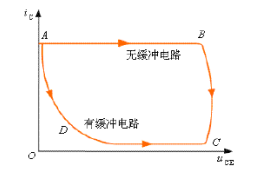
開關管由導通到截止時由于漏感L的存在,要通過R、C將其能量吸收掉,否則會產生一個尖峰電壓影響到元件的可靠性以及造成EMI問題。
整流二極管截止時還有個反向恢復電流的問題,但是把反向恢復電流最大時當作分析的起使點,那在實際分析時過程還是一樣的,只是初始狀態不同。
考慮整流二極管這個回路,設流過L上的電流為I1(t):
流過結電容Cd的電流為

流過吸收電容C的電流為

根據Cd兩端電壓等于R、C兩端電壓得到微積分方程:

由于含有積分,方程求解不便,將其求導,得到3階微分方程:

由于Cd很小,可以將其忽略以簡化分析,得到簡化后的微分方程:

考慮初始狀態I1(0)=Io,I1’(0)=(Vin-Vo)/L,其中Io為開關管關閉時電流的最大值,應用拉普拉斯變換得到變換后的方程:

這是個2階系統,應當讓其工作在過阻尼狀態防止振蕩,因此要保證極點有2個相異實根,得到

應用拉普拉斯逆變換可以得到電流I1(t)的解:

電感L上的電壓:

二極管D上的電壓:

假定L=0.1uH,C=220pF,Vo=12V,Vin= -60V(此時MOSFET ON,變壓器次級電壓反向,Vin由12V跳變為-60V),R=2*sqrt(L/C)=42.6ohm。
DCM狀態下Io=0,考慮不同的R值對波形的影響:


可以看到阻值越小,電壓電流的波形振蕩越多,峰值越高,越容易對回路產生不利影響,因此要保證工作在過阻尼狀態,電阻R不能取小。
考慮R=47ohm時不同電容C對波形的影響:


可以看到電容C越大,電壓電流變化率會減小,并且電壓的過沖會減小,這樣對EMI會有好處,但是峰值電流會變大。
考慮此時電阻R上的功率消耗,假定回路工作頻率50KHz:

可以看到正常情況下吸收電阻消耗的功率與R值大小無關,只與C及C兩端的電壓有關,因此可以看到改善EMI是以增加消耗功率為代價的,會降低回路的總體效率,因此C也不能取太大,此時P=1/2*C*(Vin-Vo)^2*f 。
需要看到此時吸收回路吸收的不是漏感L上的能量,而是電壓跳變在電容C上產生的能量。
考慮在CCM狀態下,設Io=1A和2A
C=220pF時不同R值對波形的影響:




R=47ohm時不同C值對波形的影響:




可以看到當截止電流比較大時,電阻越大電流下降越慢,吸收電容上初始電壓就會越高,對電容耐壓要求就會越高,此時電感L及二極管D兩端電壓變化也會更快,對回路產生不利影響的可能性會更大,因此吸收電阻R取值也不能太大。
吸收電容上有初始電壓是因為考慮二極管關斷時兩端電壓不能突變,電感L電流也不能突變,從而電流經吸收電阻在吸收電容上產生了初始電壓。
吸收電容的增大可以減小電壓電流的變化率。
考慮此時吸收電阻R消耗的功率:

可以看到吸收功率始終隨吸收電容C值的增大而增大,但是不同的截止電流隨吸收電阻R值的變化會有不同的變化。
因此可以根據EMI的情況選取合適的C值,然后由此C值確定R值。
可以考慮一種確定R、C值的方法,在最大截止電流的情況下確定吸收電容C上的起始電壓,這時可以計算出R值,這個R值是最大值,然后再由R值計算出C值,這時的C值是吸收電容的最小值。
考慮結二極管電容Cd的影響,設Cd=15pF:DCM狀態:Io=0,



以上是不同的吸收電阻R,考慮不同的吸收電容C:



可以看到如果吸收電阻R偏大,流過結電容的電流也會增加,并且震蕩也比較厲害,對二極管D會有不利影響,起不到保護二極管的作用。
吸收電容C的加大可以減小電壓電流的變化率。
考慮CCM狀態,Io分別為1A、2A:C=220pF,不同R的影響:






R=47ohm時不同C的影響:





可以看到截止電流越大,在二極管兩端產生的尖峰電壓越高,吸收電容越大,電壓電流變化率越小,吸收電阻越大,電壓尖峰越高。
以上的曲線是在初始狀態I(0)=Io,I’(0)=(Vin-Vo)/L,I’’(0)= -Io/Cd/L的條件下求得的,不同得初始條件會得到不同得曲線。由于該初始條件并不一定正確,因此得到的曲線可能與實際觀察到的波形會有較大差異,但是其變化趨勢是可以參考的。
-
整流二極管
+關注
關注
5文章
371瀏覽量
31311 -
等效電路
+關注
關注
6文章
292瀏覽量
32804 -
開關管
+關注
關注
4文章
226瀏覽量
21680
原文標題:工程師不看后悔:開關管吸收回路計算分析
文章出處:【微信號:Mouser-Community,微信公眾號:貿澤電子設計圈】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
開關電源電磁兼容及RC吸收回路設計
開關管吸收回路計算分析資料下載





 開關管吸收回路等效電路分析與設計
開關管吸收回路等效電路分析與設計















評論