周立功教授數年之心血之作《程序設計與數據結構》以及《面向AMetal框架與接口的編程(上)》,電子版已無償性分享到電子工程師與高校群體,書本內容公開后,在電子行業掀起一片學習熱潮。經周立功教授授權,本公眾號特對《程序設計與數據結構》一書內容進行連載,愿共勉之。
第四章為面向對象編程,本文為 4.4虛函數。
>>> 4.4.1 二叉樹
樹的應用非常廣泛,比如,數據庫就是由樹構造而成的,C編譯器的詞法分析器也是經過語法分析生成的樹。
樹是一種管理象樹干、樹枝、樹葉一樣關系的數據的數據結構,通常一棵樹由根部長出一個樹干,接著從樹干長出一些樹枝,然后樹枝上又長出更小的樹枝,而葉子則長在最細的樹枝上,樹這種數據結構正是象一棵樹倒過來的樹木。
樹是由結點(頂點)和枝構成的,由一個結點作為起點,這個起點稱為樹的根結點。從根結點上可以連出幾條枝,每條枝都和一個結點相連,延伸出來的這些結點又可以繼續通過枝延伸出新的結點。這個過程中的舊結點稱作父結點,而延伸出來的新結點稱作子結點,一個子結點都沒有的結點就叫做葉子結點。另外,從根結點出發到達某個結點所要經過的枝的個數叫做這個結點的深度。
從家譜樹血緣關系來看,家譜樹使得介紹計算機科學中用于描述樹結構的術語變得更簡單了。樹中的每一個結點都可以有幾個孩子,但是只有一個雙親。在樹中祖先和孫子的意義與日常語言中的意義完全相同。
與根形成對比的是沒有孩子的結點,這些結點稱為葉,而既不是根又不是葉的結點稱為內部結點,樹的長度定義為從根到葉的最長路徑的長度(或深度)。在一顆樹里,如果從根到葉的每條路徑的長度都大致相等,那么這顆樹被稱為平衡樹。實際上,要實現某種永遠能夠保證平衡的樹是很復雜的,這也是為什么存在多種不同種類的樹的原因。
實際上,在樹的每一層次都是分叉形式,如果任意選取樹中的一個結點和它的子樹,所得到的部分都符合樹的定義。樹中的每個結點都可以看成是以它自己為根的子樹的根,這就是樹結構的遞歸特性。如果以遞歸的觀點考察樹,那么樹只是一個結點和一個附著其上的子樹的集合——在葉結點的情景下該集合為空,因此樹的遞歸特性是其底層表示和大部分針對樹操作的算法的基礎。
樹的一個重要的子類是二叉樹,二叉樹是一種常用的樹形數據結構。二叉樹的每個結點最多只有兩個子結點(left和right),且除了根以外的其它結點,要么是雙親結點的左孩子,要么是右孩子。
>>> 4.4.2 表達式算術樹
1、問題
求解算術表達式就是一種二叉樹,它的結點包含兩種類型的對象:操作符和終值。操作符是擁有操作數的對象,終值是沒有操作數的對象。表達式樹背后的思想——存儲在父結點中的是操作符,其操作數是由子結點延伸的子樹組成的。操作數有可能是終值,或它們本身也可能是其它的表達式。表達式在子樹中展開,終值駐留在葉子結點中,這種組織形式的好處是可以通過表達式將一個表達式轉換為3種常見的表示形式:前綴、中綴和后綴,但中綴表達式是在數學中學到的最為熟悉的表達方式。在這里,將以2*(3+4)+5中綴表達式算術樹結構為例。
首先將“2*(3+4)+5”拆分為左子樹和右子樹,其中,“+” 為根節點,左子樹的值為2*(3+4),右子樹的值為5;接著將2*(3+4)拆分為左子樹和右子樹,其中,“*”為根節點,左子樹的值為2,右子樹的值為3+4;然后將3+4拆分為左子樹和右子樹,其中,“+”為根節點,左子樹的值為3,右子樹的值為4,詳見圖 4.6。注意,樹的表示法中不需要任何小括號或運算符優先級的知識,因為它描述的計算過程是唯一的。

圖 4.6 表達式算術樹
由此可見,從根結點(Node)到葉進行分析,該表達式算術樹的結點是算術運算符“+(Additive)”和“*(Multiplicative)”,它的樹葉是操作數(Number)。由于這里所有的操作都是二元(Binary)的,即每個結點最多只有兩個孩子,這顆特定的樹正好是二叉樹。因此可以用以下方式計算(calculate,簡寫為calc)每個結點:
-
如果是一個數字,則返回它的值;
-
如果是一個運算符,則計算左子樹和右子樹的值。
其計算過程是先分別輸入3和4,接著計算3+4;然后輸入2,再接著計算2*(3+4);接著輸入5,最后計算2*(3+4)+5。
傳統的做法是定義一個struct _Node,包含二元運算符和數字結點,詳見程序清單 4.12。
程序清單 4.12 表達式算術樹接口(calctree.h)

其中,使用了名為newNumNode、newAddNode和newMultNode的宏將結構體初始化,表達式算術樹接口的實現詳見程序清單 4.13。
程序清單 4.13 表達式算術樹接口的實現(cacltree.c)

表達式算術樹的使用范例詳見程序清單 4.14。
程序清單 4.14 表達式算術樹使用范例

如果此方案應用于包括上百個結點的樹時,其消耗的內存太大了。
2、抽象類
根據問題的描述,需求詞匯表中有一組這樣的概念,比如,根結點和左右葉子結點的操作數,且加法和乘法都是二元操作。雖然詞匯表對應的詞匯為Node、_pLeft、_pRight、Number、Binary、Additive和Multiplicative,但用Node、_pLeft、_pRight、NumNode、BinNode、AddNode和MultNode描述表達式算術樹的各個結點更準確。
由于AddNode和MultNode都是二元操作,其共性是兩個數(_pLeft和_pRight)的計算,其可變性分別為加法和乘法,因此可以將它們的共性包含在BinNode中,可變性分別包含在AddNode和MultNode中。
其實輸入操作數同樣可以視為計算,因此NumNode和BinNode的共性也是計算,不妨將它們的共性上移到Node抽象類中。
顯然,基于面向對象的C編程,則表達式算術樹的所有結點都是從類Node繼承的子類,Node的直系后代為NumNode和BinNode,NumNode表示一個數,BinNode表示一個二元運算,然后再從BinNode派生兩個類:AddNode和MultNode。
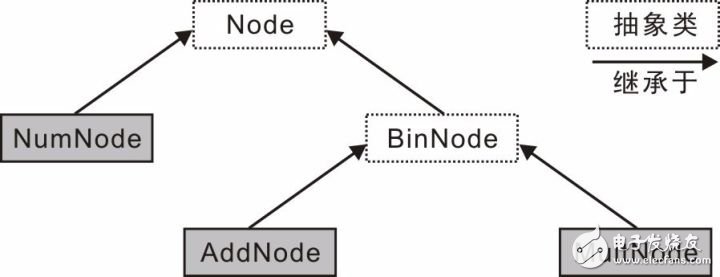
圖 4.7 結點的類層次
如圖 4.7所示展示了類的層次性,它們是一種“is-a”的抽象層次結構,子類AddNode和MultNode重新定義了BinNode和Node基類的結構和行為。基類代表了一般化的抽象,子類代表了特殊的抽象。雖然抽象類Node或BinNode不能實例化,只能作為其它類的父類,但NumNode、AddNode和MultNode子類是可以實例化的。Node抽象類的定義如下:

除了Node之外,每個子類都要實現自己的nodeCalc計算方法,并返回一個作為計算結點值的雙精度數。即:

其中的NumNode結點是從Node分出來的,_num表示數值。BinNode也是從Node分出來的,_pLeft和_pRight分別為指向左子樹和右子樹的指針,而AddNode和MultNode又是從BinNode分出來的。
此前,針對繼承和多態框架,使用了一種稱為靜態的初始化范型。在這里,將使用動態內存分配初始化范型處理繼承和多態框架。
3、建立接口
由于對象不同,因此動態分配內存的方式不一樣,但其共性是——不再使用某個對象時,釋放動態內存的方法是一樣,因此還需要添加一個node_cleanup()函數,這是通過free()實現的,詳見程序清單 4.15。
程序清單 4.15 表達式算術樹的接口(CalcTree1.h)

實現表達式算術樹的第一步是輸入數據和初始化NumNode結構體的變量isa和_num,newNumNode()函數原型如下:
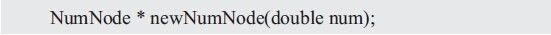
其調用形式如下:

接下來開始為計算做準備,node_calc()函數原型如下:

其調用形式如下:

然后開始進行加法運算,newAddNode()函數原型如下:

其調用形式如下:

當然,也可以開始進行乘法運算了,newMultNode()函數原型如下:
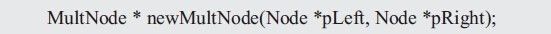
其調用形式如下:

一切準備就緒,則計算最終結果并釋放不再使用的資源,node_cleanup()函數原型如下:

其調用形式如下:

4、實現接口
顯然,為每個結點創建了相應的類后,就可以為每個結點創建一個動態變量,即可在運行時根據需要使用malloc()分配內存并使用指針存儲該地址,并使用指針初始化結構體的各個成員,CalcTree1.c接口的實現詳見程序清單 4.16。
程序清單 4.16表達式算術樹接口的實現(CalcTree1.c)

>>> 4.4.3 虛函數
雖然可以使用繼承實現表達式算術樹,但實現代碼中的每個對象都有函數指針。如果結構體內有很多函數指針,或必須生成更多的對象時,將會出現多個對象具有相同的行為、需要較多的函數指針和需要生成較多數量的對象,將會浪費很多的內存。
不妨將Node中的成員轉移到另一個結構體中實現一個虛函數表,然后在接口中創建一個抽象數據類型NodeVTable,在此基礎上定義一個指向該表的指針vtable。比如:

表達式算術樹的接口詳見程序清單 4.17,其中的NumNode派生于Node,_num表示數值;BinNode也是派生于Node,pLeft和pRight分別表示指向左子樹和右子樹的指針;而AddNode和MultNode又派生于BinNode。雖然抽象類包含一個或多個純虛函數類,但不能實例化(此類沒有對象可創建),只有從一個抽象類派生的類和為所有純虛函數提供了實現代碼的類才能實例化,它們都必須提供自己的計算方法node_calc和node_cleanup。
程序清單 4.17 表達式算術樹接口(CalcTree2.h)

顯然,為每個結點創建了相應的類后,就可以為每個結點創建一個動態變量,即可在運行時根據需要使用malloc()分配內存并使用指針存儲該地址,并使用指針初始化結構體的各個成員,表達式算術樹接口的實現詳見程序清單 4.18。
程序清單 4.18 表達式算術樹接口的實現(CalcTree2.c)

-
周立功
+關注
關注
38文章
130瀏覽量
37672 -
虛函數
+關注
關注
0文章
8瀏覽量
1713
原文標題:周立功:深入理解虛函數
文章出處:【微信號:ZLG_zhiyuan,微信公眾號:ZLG致遠電子】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何用C語言實現面向對象編程
plc面向對象編程架構與實現




 面向對象編程——虛函數
面向對象編程——虛函數












評論