采用奇校驗,則在數據后補上個0,數據變為0001 1010 0,數據中1的個數為奇數個(3個)
采用偶校驗,則在數據后補上個1,數據變為0001 1010 1,數據中1的個數為偶數個(4個)
接收方通過計算數據中1個數是否滿足奇偶性來確定數據是否有錯。奇偶校驗的缺點也很明顯,首先,它對錯誤的檢測概率大約只有50%。也就是只有一半的錯誤它能夠檢測出來。另外,每傳輸一個字節都要附加一位校驗位,對傳輸效率的影響很大。因此,在高速數據通訊中很少采用奇偶校驗。奇偶校驗優點也很明顯,它很簡單,因此可以用硬件來實現,這樣可以減少軟件的負擔。因此,奇偶校驗也被廣泛的應用著。奇偶校驗就先介紹到這來,之所以從奇偶校驗說起,是因為這種校驗方式最簡單,而且后面將會知道奇偶校驗其實就是CRC 校驗的一種(CRC-1)。累加和校驗另一種常見的校驗方式是累加和校驗。所謂累加和校驗實現方式有很多種,最常用的一種是在一次通訊數據包的最后加入一個字節的校驗數據。這個字節內容為前面數據包中全部數據的忽略進位的按字節累加和。比如下面的例子:
我們要傳輸的信息為: 6、23、4
加上校驗和后的數據包:6、23、4、33
這里 33 為前三個字節的校驗和。接收方收到全部數據后對前三個數據進行同樣的累加計算,如果累加和與最后一個字節相同的話就認為傳輸的數據沒有錯誤。累加和校驗由于實現起來非常簡單,也被廣泛的采用。但是這種校驗方式的檢錯能力也比較一般,對于單字節的校驗和大概有1/256 的概率將原本是錯誤的通訊數據誤判為正確數據。之所以這里介紹這種校驗,是因為CRC校驗在傳輸數據的形式上與累加和校驗是相同的,都可以表示為:通訊數據 校驗字節(也可能是多個字節)初識 CRC 算法CRC 算法的基本思想是將傳輸的數據當做一個位數很長的數。將這個數除以另一個數。得到的余數作為校驗數據附加到原數據后面。還以上面例子中的數據為例:6、23、4 可以看做一個2進制數: 0000011000010111 00000010
假如被除數選9,二進制表示為:1001
則除法運算可以表示為:
可以看到,最后的余數為1。如果我們將這個余數作為校驗和的話,傳輸的數據則是:6、23、4、1
CRC 算法和這個過程有點類似,不過采用的不是上面例子中的通常的這種除法。在CRC算法中,將二進制數據流作為多項式的系數,然后進行的是多項式的乘除法。還是舉個例子吧。比如說我們有兩個二進制數,分別為:1101 和1011。1101 與如下的多項式相聯系:1x3+1x2+0x1+1x0=x3+x2+x01011與如下的多項式相聯系:1x3+0x2+1x1+1x0=x3+x1+x0兩個多項式的乘法:(x3+x2+x0)(x3+x1+x0)=x6+x5+x4+x3+x3+x3+x2+x1+x0
得到結果后,合并同類項時采用模2運算。也就是說乘除法采用正常的多項式乘除法,而加減法都采用模2運算。所謂模2運算就是結果除以2后取余數。比如3 mod 2 = 1。因此,上面最終得到的多項式為:x6+x5+x4+x3+x2+x1+x0,對應的二進制數:111111
加減法采用模2運算后其實就成了一種運算了,就是我們通常所說的異或運算:
上面說了半天多項式,其實就算是不引入多項式乘除法的概念也可以說明這些運算的特殊之處。只不過幾乎所有講解 CRC 算法的文獻中都會提到多項式,因此這里也簡單的寫了一點基本的概念。不過總用這種多項式表示也很羅嗦,下面的講解中將盡量采用更簡潔的寫法。
除法運算與上面給出的乘法概念類似,還是遇到加減的地方都用異或運算來代替。下面是一個例子:
要傳輸的數據為:1101011011
除數設為:10011
在計算前先將原始數據后面填上4個0:11010110110000,之所以要補0,后面再做解釋。
從這個例子可以看出,采用了模2的加減法后,不需要考慮借位的問題,所以除法變簡單了。最后得到的余數就是CRC 校驗字。為了進行CRC運算,也就是這種特殊的除法運算,必須要指定個被除數,在CRC算法中,這個被除數有一個專有名稱叫做“生成多項式”。生成多項式的選取是個很有難度的問題,如果選的不好,那么檢出錯誤的概率就會低很多。好在這個問題已經被專家們研究了很長一段時間了,對于我們這些使用者來說,只要把現成的成果拿來用就行了。
最常用的幾種生成多項式如下:CRC8=X8+X5+X4+X0CRC-CCITT=X16+X12+X5+X0CRC16=X16+X15+X2+X0CRC12=X12+X11+X3+X2+X0CRC32=X32+X26+X23+X22+X16+X12+X11+X10+X8+X7+X5+X4+X2+X1+X0有一點要特別注意,文獻中提到的生成多項式經常會說到多項式的位寬(Width,簡記為W),這個位寬不是多項式對應的二進制數的位數,而是位數減1。比如CRC8中用到的位寬為8的生成多項式,其實對應得二進制數有九位:
100110001。另外一點,多項式表示和二進制表示都很繁瑣,交流起來不方便,因此,文獻中多用16進制簡寫法來表示,因為生成多項式的最高位肯定為1,最高位的位置由位寬可知,故在簡記式中,將最高的1統一去掉了,如CRC32的生成多項式簡記為04C11DB7實際上表示的是104C11DB7。當然,這樣簡記除了方便外,在編程計算時也有它的用處。對于上面的例子,位寬為4(W=4),按照CRC算法的要求,計算前要在原始數據后填上W個0,也就是4個0。位寬W=1的生成多項式(CRC1)有兩種,分別是X1和X1+X0,讀者可以自己證明10 對應的就是奇偶校驗中的奇校驗,而11對應則是偶校驗。
因此,寫到這里我們知道了奇偶校驗其實就是CRC校驗的一種特例,這也是我要以奇偶校驗作為開篇介紹的原因了。CRC算法的編程實現說了這么多總算到了核心部分了。從前面的介紹我們知道CRC校驗核心就是實現無借位的除法運算。下面還是通過一個例子來說明如何實現CRC校驗。
假設我們的生成多項式為:100110001(簡記為0x31),也就是CRC-8則計算步驟如下:
(1)將CRC寄存器(8-bits,比生成多項式少1bit)賦初值0(2)在待傳輸信息流后面加入8個0(3)While (數據未處理完)(4)Begin(5)If (CRC寄存器首位是1)(6)reg = reg XOR 0x31(7)CRC寄存器左移一位,讀入一個新的數據于CRC寄存器的0 bit的位置。(8)End(9)CRC寄存器就是我們所要求的余數。實際上,真正的CRC 計算通常與上面描述的還有些出入。這是因為這種最基本的CRC除法有個很明顯的缺陷,就是數據流的開頭添加一些0并不影響最后校驗字的結果。這個問題很讓人惱火啊,因此真正應用的CRC 算法基本都在原始的CRC算法的基礎上做了些小的改動。
所謂的改動,也就是增加了兩個概念,第一個是“余數初始值”,第二個是“結果異或值”。
所謂的“余數初始值”就是在計算CRC值的開始,給CRC寄存器一個初始值。“結果異或值”是在其余計算完成后將CRC寄存器的值在與這個值進行一下異或操作作為最后的校驗值。
常見的三種CRC 標準用到個各個參數如下表。

上面的代碼是我從http://mdfs.net/Info/Comp/Comms/CRC16.htm找到的,不過原始代碼有錯誤,我做了些小的修改。
下面對這個函數給出個例子片段代碼:讀者可以驗算,c1、c2 的結果都為 29b1。上面代碼中crc 的初始值之所以為0xffff,是因為CCITT標準要求的除數初始值就是0xffff。
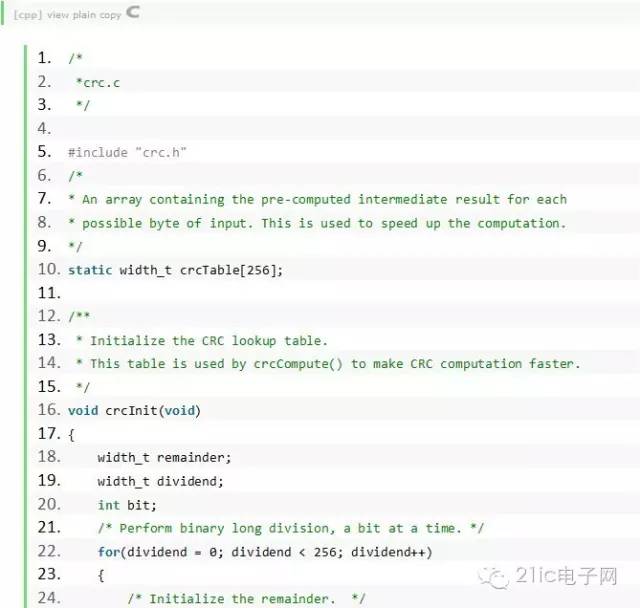
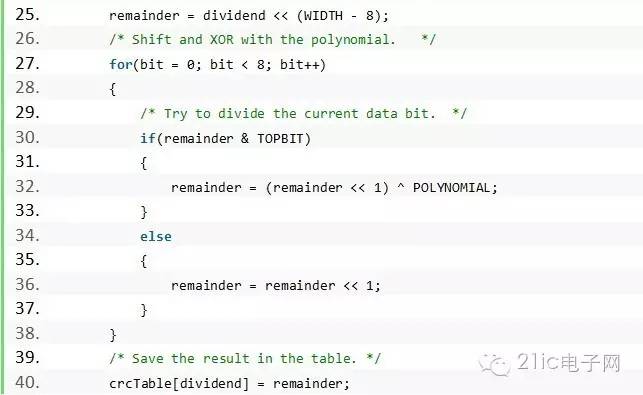
上面的算法對數據流逐位進行計算,效率很低。實際上仔細分析CRC計算的數學性質后我們可以多位多位計算,最常用的是一種按字節查表的快速算法。該算法基于這樣一個事實:計算本字節后的CRC碼,等于上一字節余式CRC碼的低8位左移8位,加上上一字節CRC右移 8位和本字節之和后所求得的CRC碼。如果我們把8位二進制序列數的CRC(共256個)全部計算出來,放在一個表里,編碼時只要從表中查找對應的值進行處理即可。
按照這個方法,可以有如下的代碼(這個代碼也不是我寫的,是我在Micbael Barr的書“Programming Embedded Systems in C and C++” 中找到的,同樣,我做了點小小的改動。):

-
CRC校驗
+關注
關注
0文章
84瀏覽量
15207 -
CRC算法
+關注
關注
0文章
15瀏覽量
8849
原文標題:嵌入式程序員的循環冗余校驗(CRC)算法最簡單入門
文章出處:【微信號:weixin21ic,微信公眾號:21ic電子網】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
新手怎么學嵌入式?
如何使用 RISC-V 進行嵌入式開發
基于Xilinx ZYNQ7000 FPGA嵌入式開發實戰指南
零基礎嵌入式開發學習路線
嵌入式開發常見問題排查

【「ARM MCU嵌入式開發 | 基于國產GD32F10x芯片」閱讀體驗】+書籍整體概況
聚焦嵌入式開發中的合規性工具、項目管理工具、版本迭代工具應用
嵌入式開發者的未來





 嵌入式開發的crc算法知識精選
嵌入式開發的crc算法知識精選











評論