短期不穩定的原因
l約翰遜噪聲(熱誘導電荷波動,即電阻元件中的“熱電動勢”)
l缺陷和量子漲落引起的聲子散射(與Q有關)
l振蕩器電路(有源和無源元件)產生的噪聲
l溫度波動-熱瞬態效應
活動在烤箱設定點下降
l隨機振動
l吸附分子數量的波動
l應力釋放、界面波動(石英、電極、安裝、粘合)
l原子頻率標準中的散粒噪聲
字母 l(英語字母表中的第十二個字母)
Allan偏差
也稱為雙樣本偏差,或“艾倫方差”的平方根,它是描述時域中振蕩器短期穩定性的標準方法。用σy(τ)表示,
where
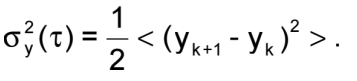
分數頻率是在
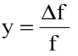
一段時間內測量的
間隔,τ;(yk+1-yk)是成對的
y的連續測量,理想情況下,<>表示無窮多(yk+1-yk)2的時間平均值。通過有限數量的m次測量可以獲得一個很好的估計
(m≥100)。
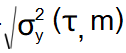
通常表示·,即。
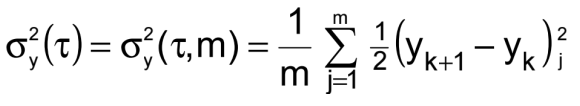
為什么σy(τ)?
經典方差:
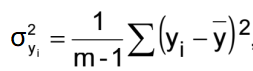
一些常見的噪聲發散
隨機游走等過程,即方差隨著數據點數量的增加而增加。
l艾倫方差:
?精密振蕩器中觀察到的所有噪聲過程的收斂。
?與冪律譜密度類型有直接關系。
?易于計算。
?在估計噪聲過程方面比快速傅里葉變換更快、更準確。
頻率噪聲和σy(τ)
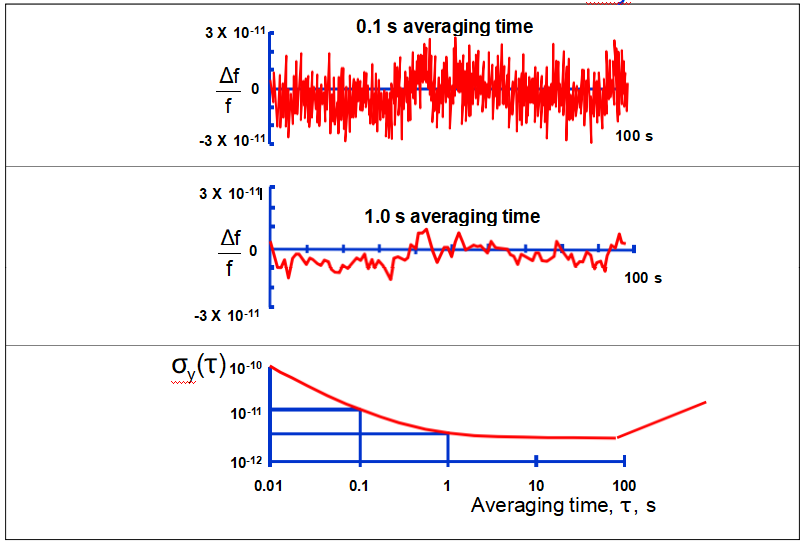
時域穩定性
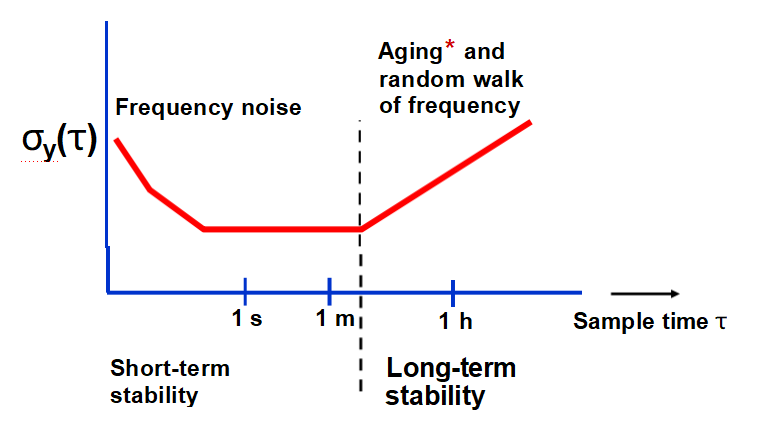
*為了使σy(τ)成為隨機頻率波動的適當度量,必須從長τ的數據中適當地減去老化。
σy(τ)的冪律依賴性
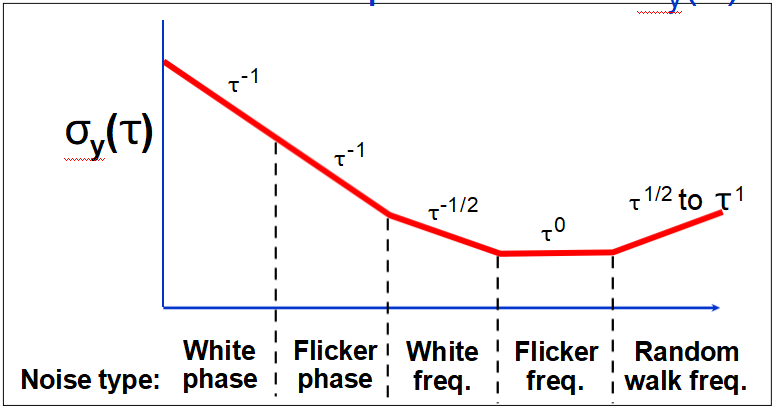
在頻率噪聲閃爍(即“閃爍基底”)區域以下,晶體振蕩器通常表現出τ-1(白相位噪聲)依賴性。原子
標準顯示τ-1/2(白頻噪聲)依賴性低至約
伺服回路時間常數,τ-1依賴性小于該時間常數。
閃爍下限開始時的典型τ為:晶體振蕩器為1s,晶體振蕩器為103s
Rb標準和Cs標準的105s。在τ較大的情況下,頻率和老化的隨機游走占主導地位。
噪音圖片
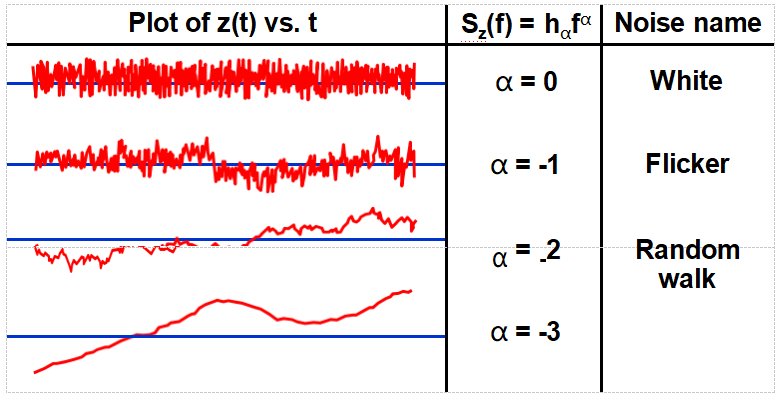
圖表顯示了量z(t)的波動,例如,可以是計數器的輸出(Δf vs.t)或相位檢測器的輸出(φ[t]vs.t。這些圖顯示了模擬的時域行為
對應于最常見的(冪律)光譜密度;hα是振幅
系數。注:由于SΔf=f2Sφ,例如白頻噪聲和相位隨機游走是等效的。
譜密度
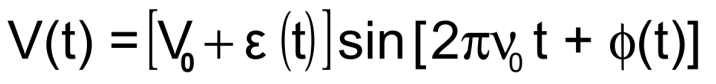
在頻域中,由于相位偏差φ(t),一些
功率在ν0以外的頻率。穩定性為
以“光譜密度”為特征。光譜密度SV(f)
在以f為中心的單位帶寬內,均方電壓不是衡量頻率穩定性的好方法,因為ε(t)和φ(t)都對頻率穩定性有貢獻,而且它與頻率波動沒有唯一關系
(盡管ε(t)在精密頻率源中通常可以忽略不計。)
相位和分數頻率波動的譜密度Sφ(f)和Sy(f)分別用于測量
頻域。量g(t)的譜密度Sg(f)是以f為中心的單位帶寬中g(t的均方值。此外,
帶寬BW中g2的RMS值由下式給出
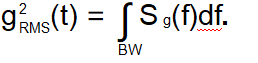
混音器功能

相位檢測器
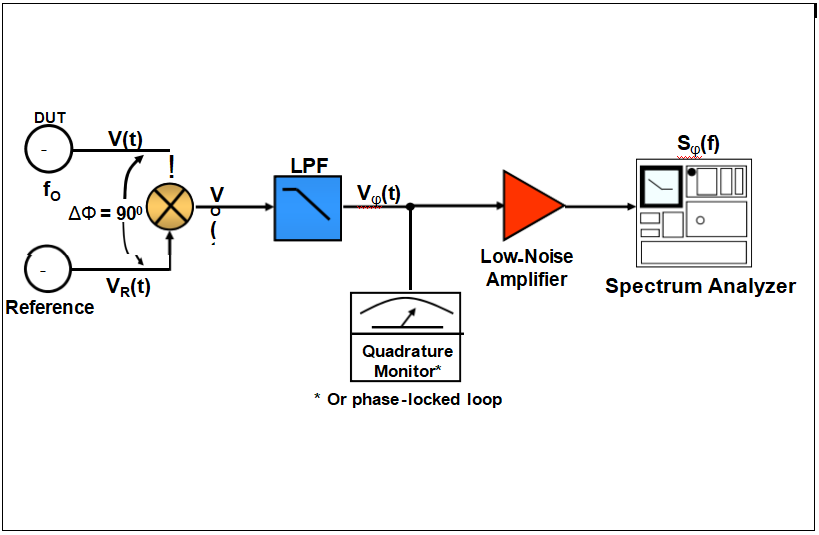
相位噪聲測量
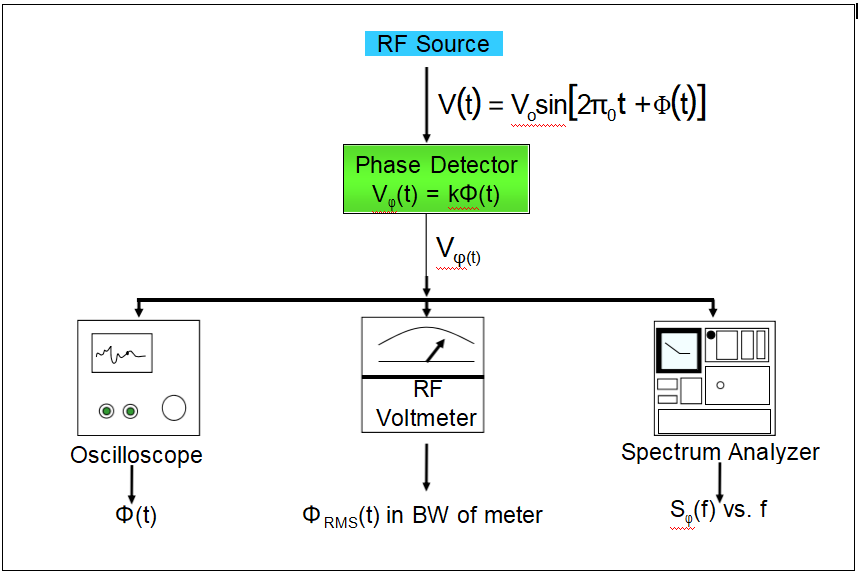
頻率-相位-時間關系

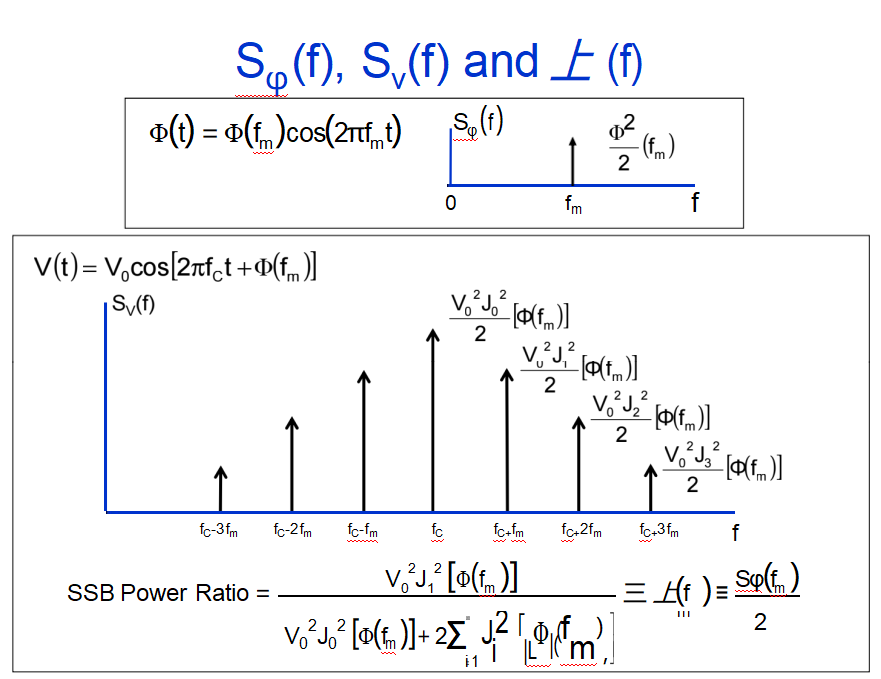
相位噪聲的類型
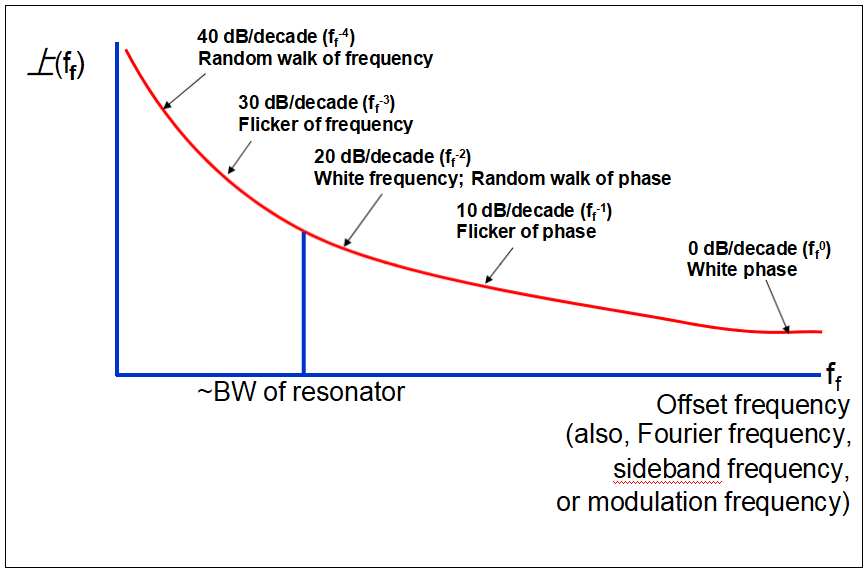
晶體振蕩器中的噪聲
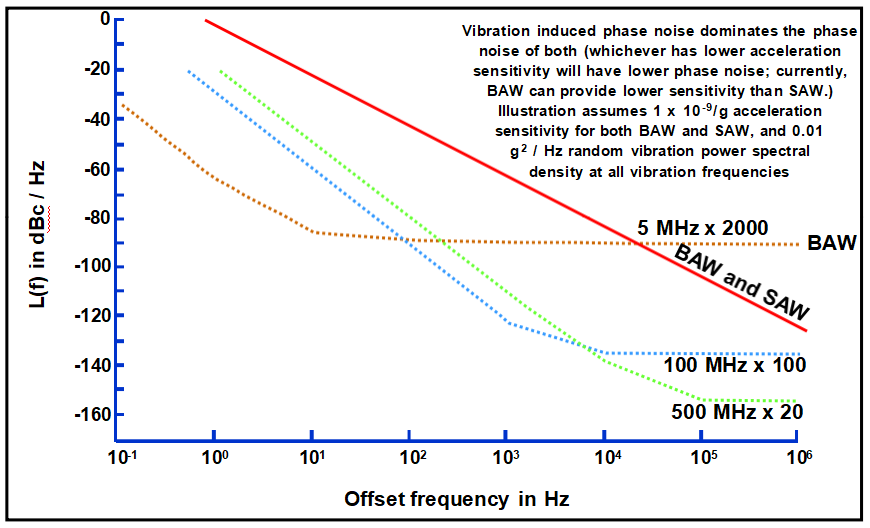
l頻率乘以N會使相位噪聲增加N2(即增加20log N,單位為dB)。
l在許多應用中,振動引起的“噪聲”主導了所有其他噪聲源(見后面的加速度效應部分)。
l靠近載波(在諧振器的BW內),Sy(f)變化為1/f,Sφ(f)為1/f3,其中f=與載波頻率的偏移,ν。Sφ(f)也隨1/Q4變化,其中Q=無負載Q
l Qmaxν=常數。,Sφ(f)≠ν4。(Qmaxν)BAW=1.6 x 1013赫茲;(Qmaxν)聲表面波=1.05 x 1013赫茲。
σy(τ)隨τ-1和τ-1/2變化的區域(τ-1/2出現在原子頻率標準中),
σy(τ)├(QSR)-1,其中SR是信噪比;即,Q和信噪比越高,短期穩定性越好(頻域中遠離載波的相位噪聲也越好)。
l當振蕩器維持電路是一個重要的噪聲源時,諧振器的負載Q會影響噪聲。
噪聲基底受約翰遜噪聲的限制;噪聲功率,kT=-174 dBm/Hz,290K
l更高的信號電平可以改善噪聲基底,但不能改善近距離噪聲。(事實上,高驅動電平通常會降低近距離噪聲,原因尚不完全清楚。)
l低噪聲SAW與低噪聲BAW相乘:BAW在f<~1kHz時噪聲較低,SAW在f>~1kHz時噪音較低;可以對兩者進行鎖相,以獲得兩者的最佳效果。
低噪聲SAW和BAW倍增至10 GHz
(在非振動環境中)
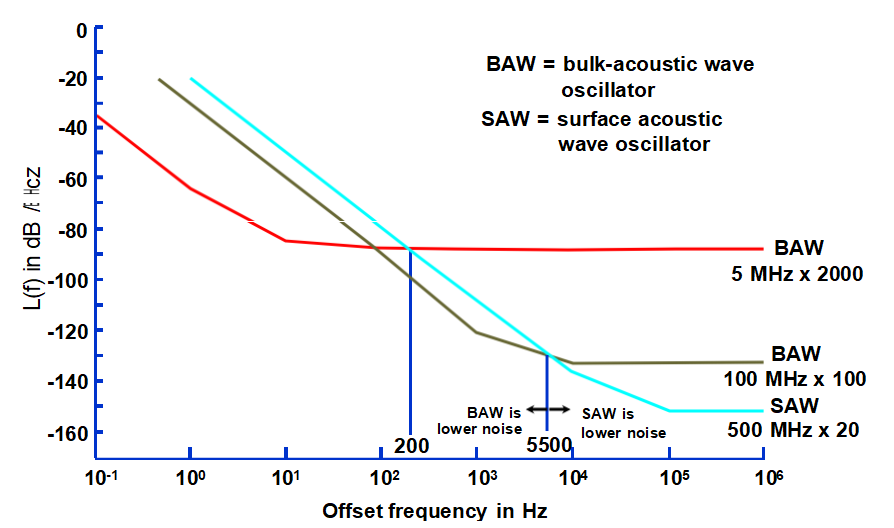
低噪聲SAW和BAW倍增至10 GHz
(在振動環境中)
TCXO噪聲
TCXO的短期穩定性取決于溫度(T),通常比OCXO差,原因如下:
?TCXO晶體的頻率(f)與T的斜率隨T而變化。例如,在~20℃時,f與T的坡度可能接近零,但在T的極端值時,它將為~1ppm/oC。T
波動將在實驗室環境T下引起較小的f波動,因此穩定性可能很好,但毫度波動將在T極值處引起~10-9 f波動。TCXO的f與T斜率也隨T而變化;零點和最大值可以在任何T處
最大斜率約為1ppm/oC。
?AT切割晶體的熱瞬態敏感性使T波動的影響不僅取決于T,還取決于T的變化率(而SC切割晶體
通常用于精密OCXO對熱瞬變不敏感)。在變化的T條件下,T傳感器(熱敏電阻)和晶體之間的T梯度會加劇問題。
?TCXO通常使用基模AT切割晶體,其Q值低于OCXO中通常使用的晶體,C1值大于OCXO中使用的晶體。Q越低,晶體本身就越嘈雜,而C1越大,振蕩器對電路噪聲越敏感。
?AT切割晶體的f與T通常表現出活性下降(見本文后面的“活性下降”
第章)。在出現驟降的T處,f與T的斜率可能非常高,因此T波動引起的噪聲也會非常高,例如,σy(τ)可能降低100倍,相位噪聲可能降低30 dB。任何T點都可能出現活動下降。
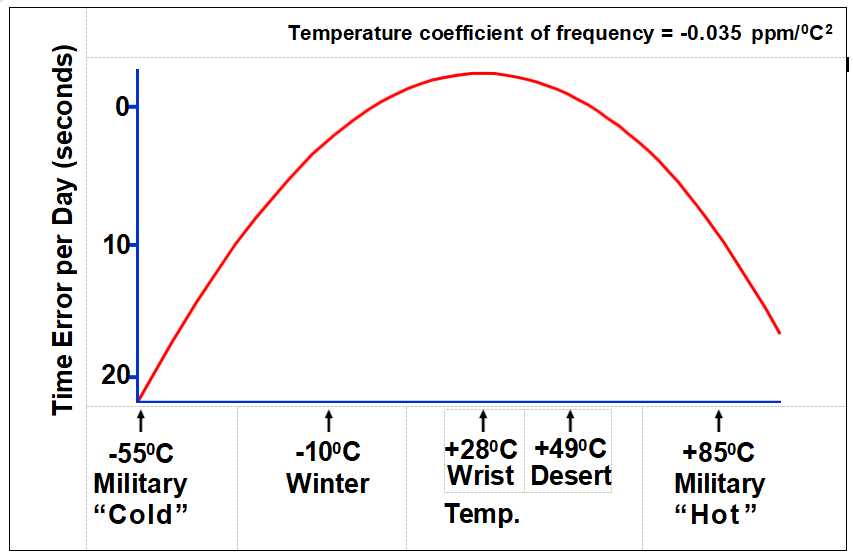
石英手表精度與溫度
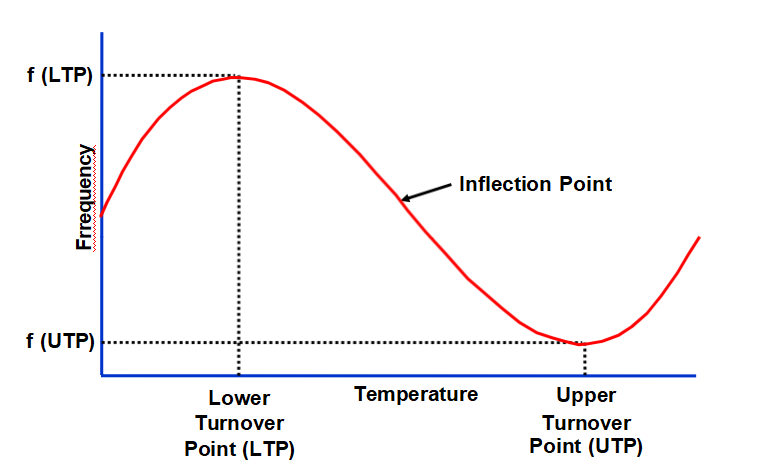
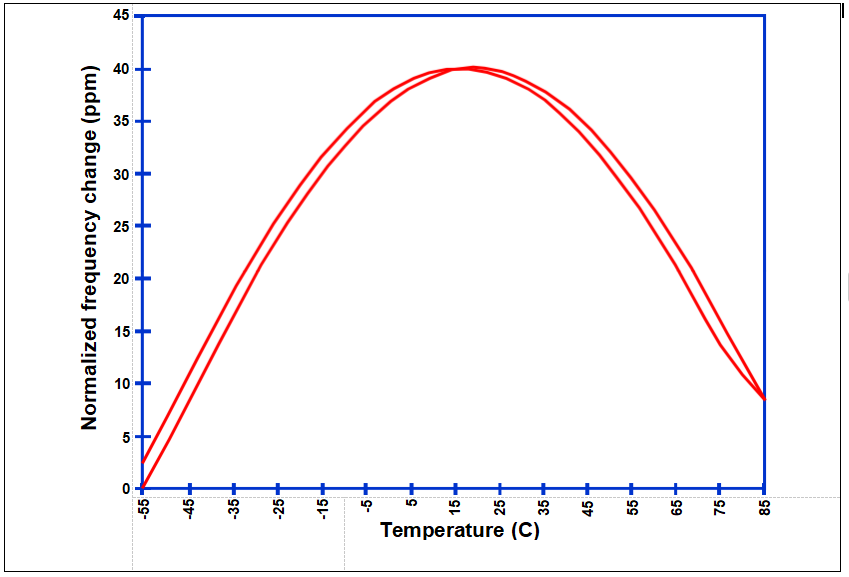
頻率與溫度特性
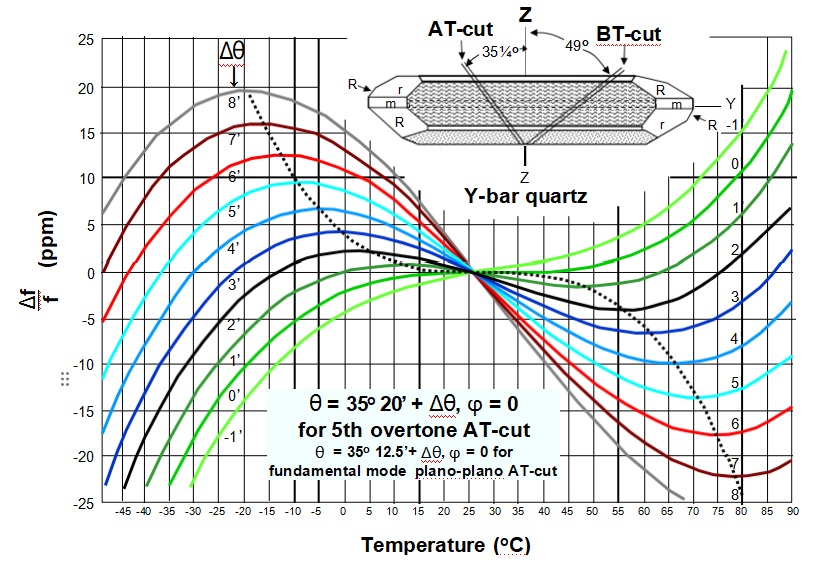
諧振器f與T的決定因素
主要:切割角度
l中學:
?Overtone
?空白幾何形狀(輪廓、尺寸比)
?材料雜質和應變
?安裝和粘合應力(大小和方向)
?電極(尺寸、形狀、厚度、密度、應力)
?駕駛水平
?干擾模式
?負載電抗(值和溫度系數)
?溫度變化率
?熱歷史
?電離輻射
頻率溫度與切割角度,AT切割
OCXO應用中SC截止諧振器的期望f與T
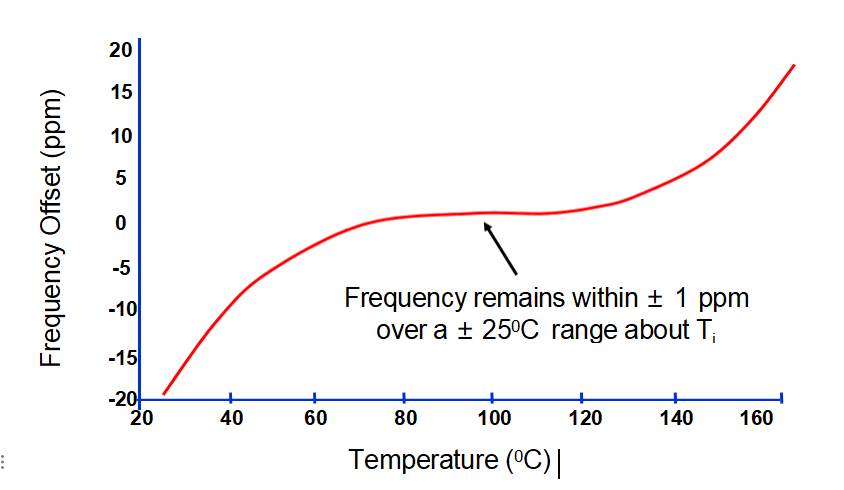
OCXO烘箱對穩定性的影響
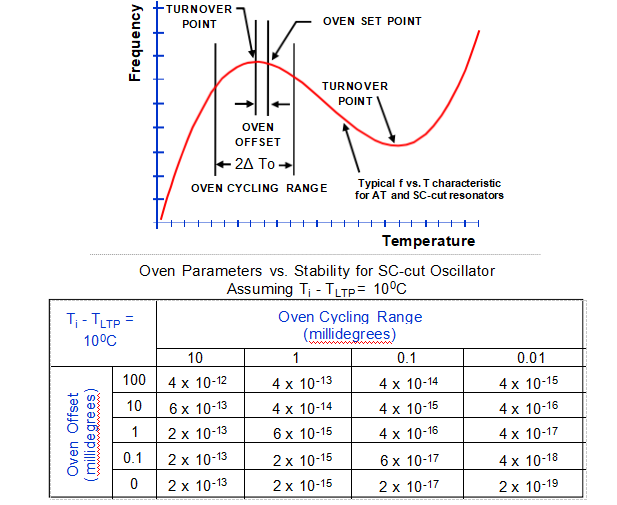
AT和其他非熱瞬態補償振蕩器切割的比較表沒有意義,因為動態f與T效應通常會主導靜態f與T效果。
烘箱穩定性限制
?通過前饋補償技術實現了105的熱增益(即,在外殼T外測量并調整熱敏電阻的設定值以進行預測和
補償),并配有雙烤箱。例如,當增益為105時,如果外部ΔT=100oC,內部ΔT=1 mK。
?良好放大器的穩定性~1μK/K
?熱敏電阻的穩定性約為1mK/年至100mK/年
?噪聲<1μK(熱敏電阻中的約翰遜噪聲+放大器噪聲+橋電流中的散粒噪聲)
?溫度波動的量子極限~1nK
?最佳的烤箱設計可以提供非常高的f與T穩定性
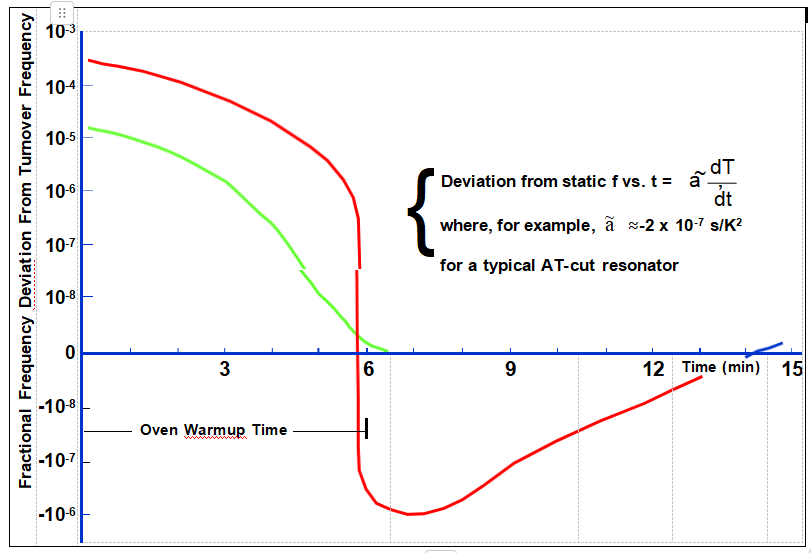
AT和SC切割諧振器的預熱
TCXO熱滯后
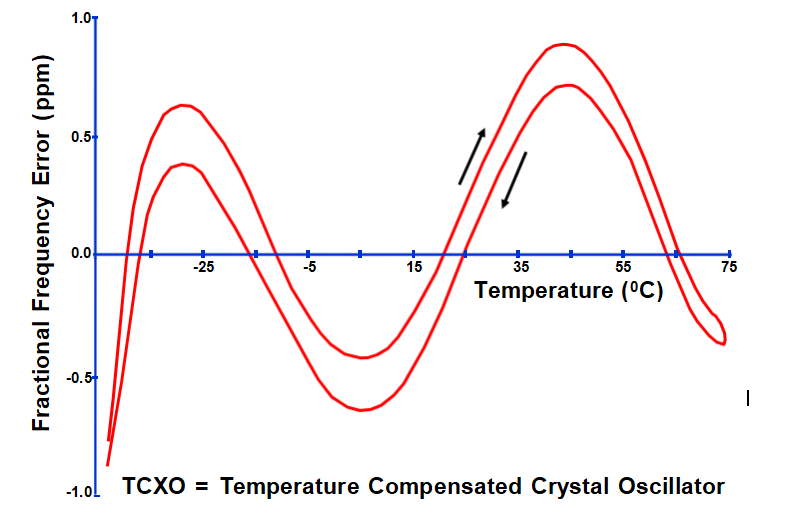
明顯滯后
OCXO收回
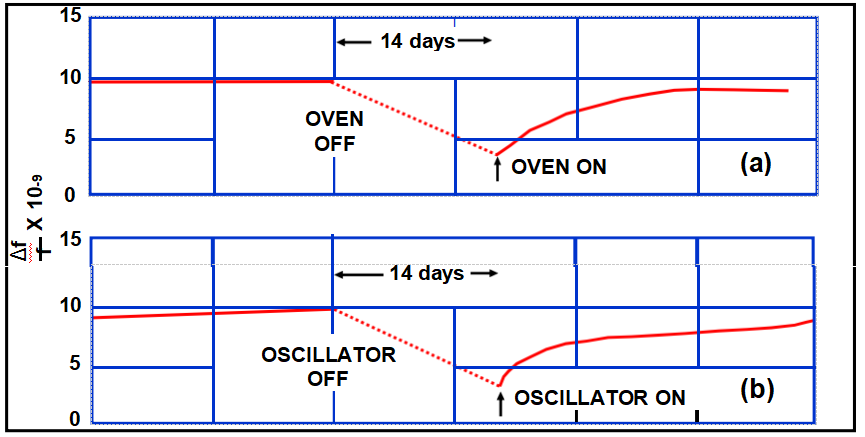
在(a)中,振蕩器在烤箱關閉和打開的同時持續打開。在(b)中,烤箱在振蕩器關閉和打開時持續打開。
TCXO微調效果
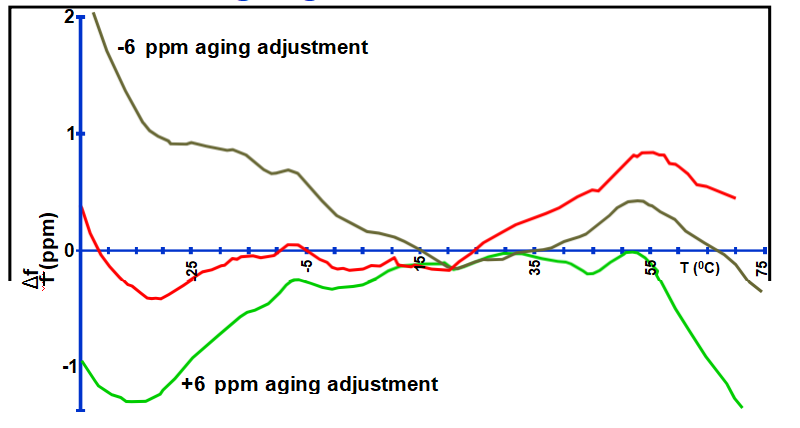
在TCXO中,溫度敏感電抗用于補償f與T的關系
變化。可變電抗也用于補償TCXO老化。老化調整對f與T穩定性的影響是“微調效應”。曲線顯示f與T
零微調和±6ppm微調時“0.5ppm TCXO”的穩定性。(為清楚起見,曲線已垂直位移。)
為什么有修剪效果?
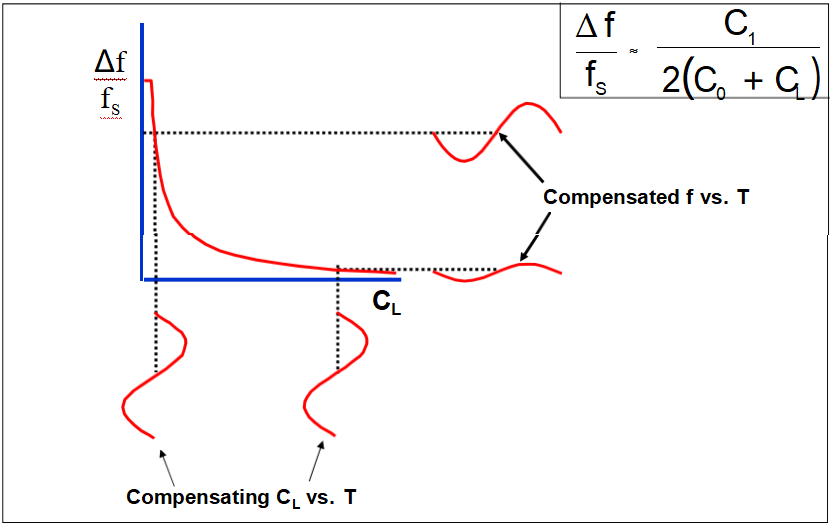
負載電容對f與T的影響
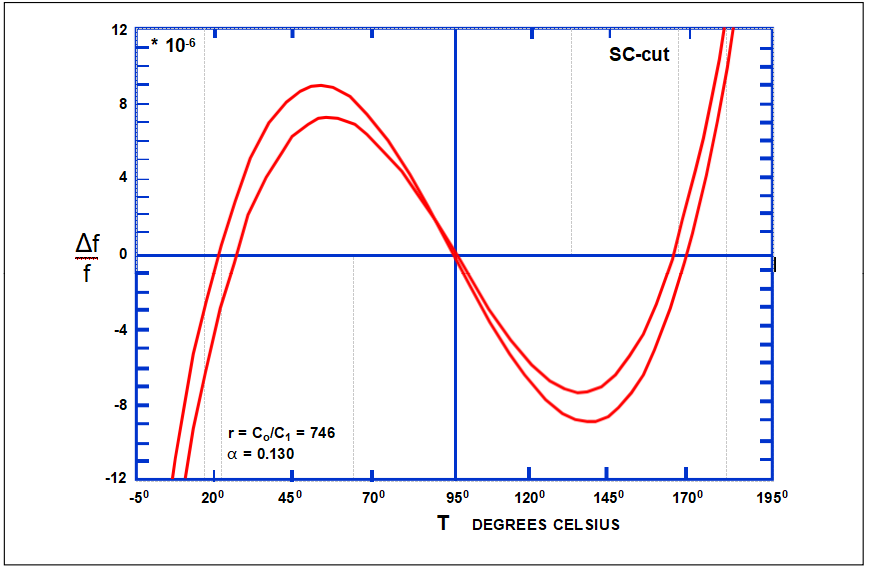
諧波對f與T的影響
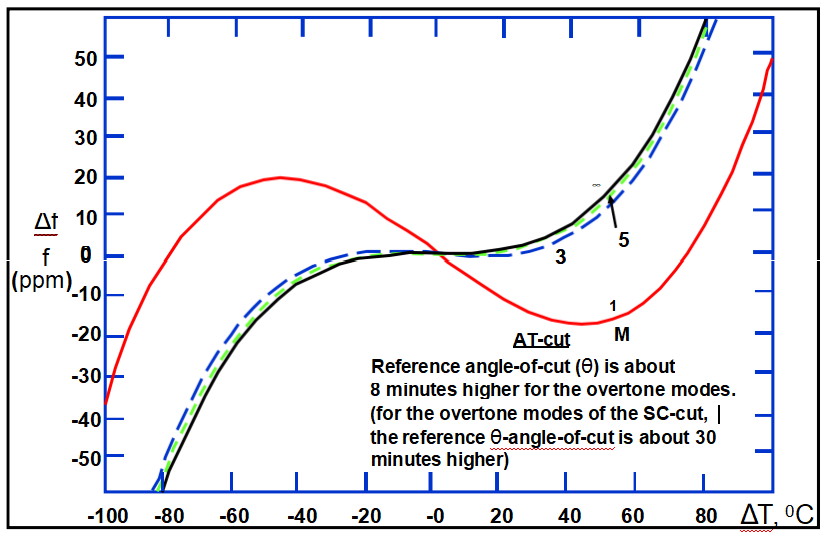
幅頻效應
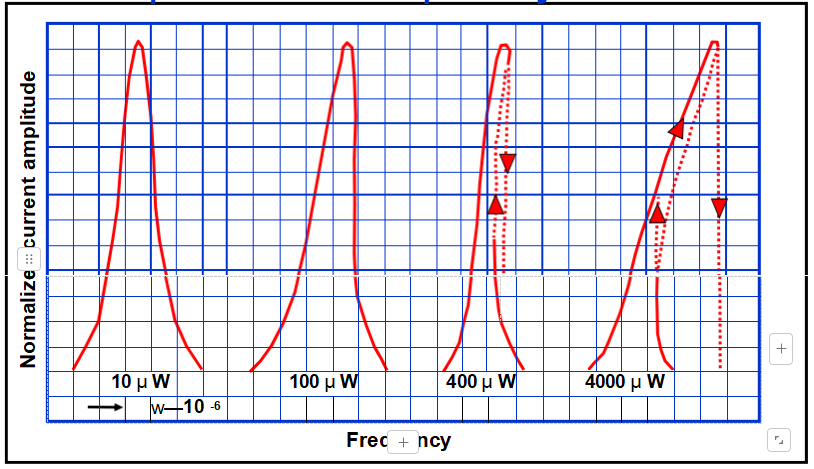
在高驅動水平下,由于石英的非線性,共振曲線變得不對稱。
頻率與驅動電平
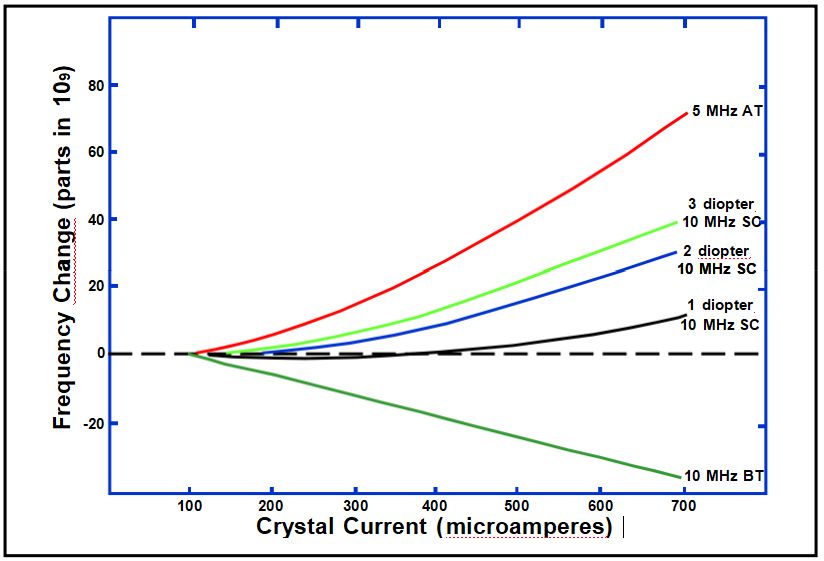
驅動水平與阻力
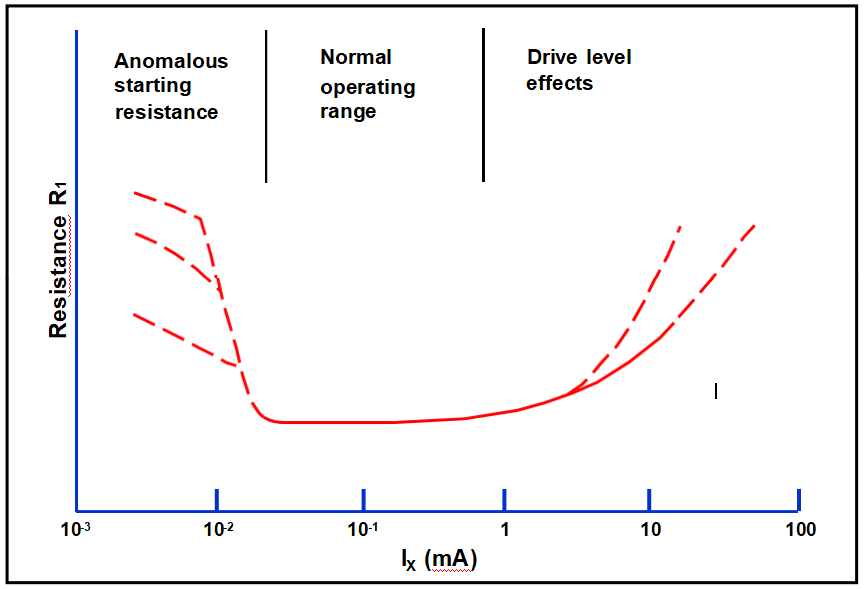
第二級驅動效應
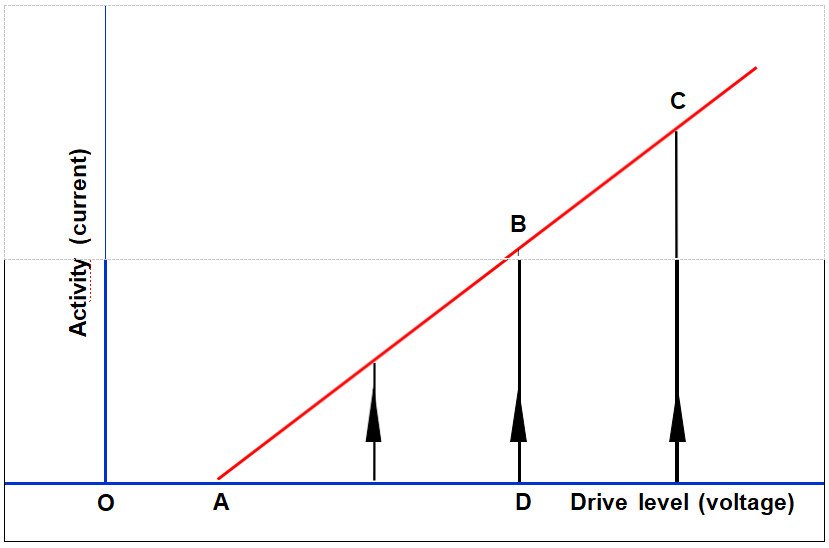
活動下降
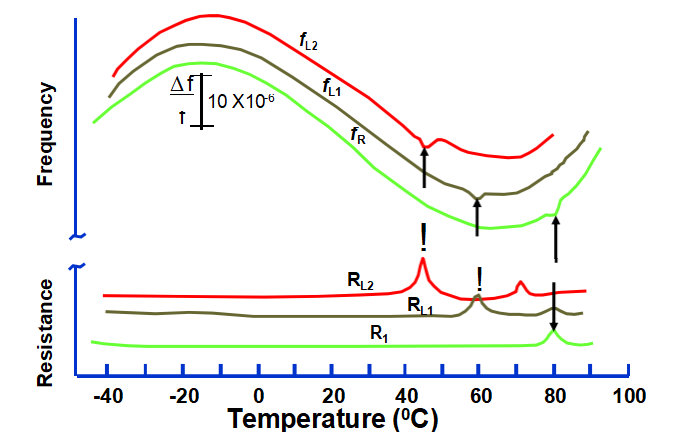
在有負載和無負載運行時,f與T和R與T的活動下降
電容器。浸入溫度是CL的函數,這表明浸入是由具有較大負溫度系數的模式(可能是彎曲)引起的。
頻率跳躍
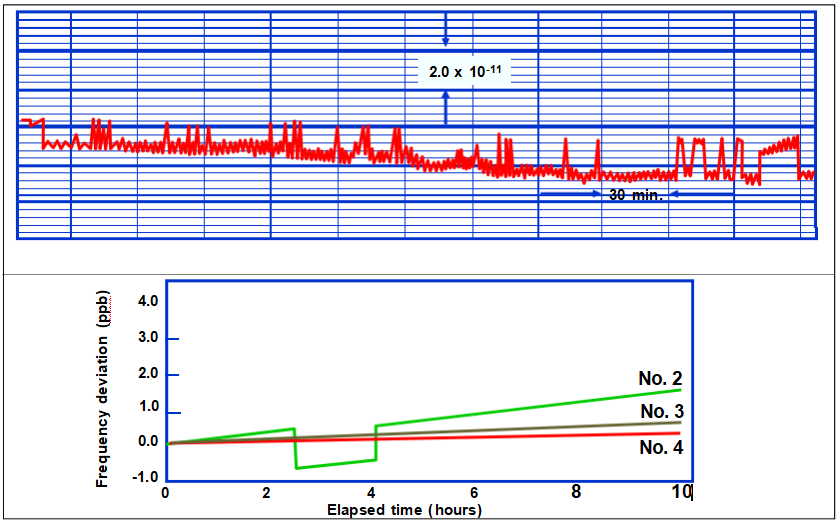
加速度與頻率變化
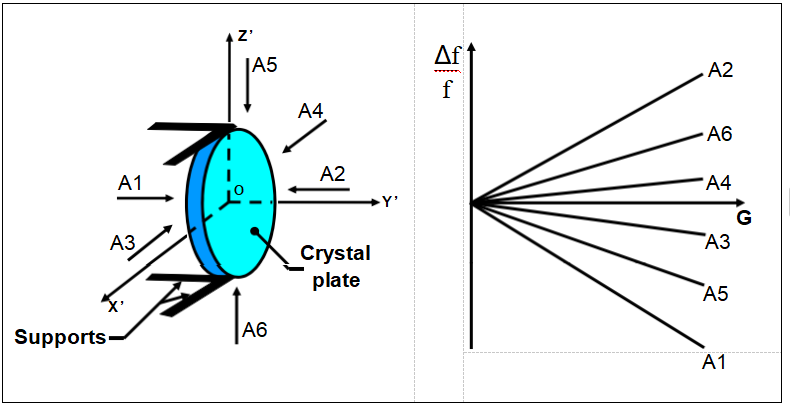
頻率偏移是幅度和方向的函數
并且通常與高達至少50gs的幅度呈線性關系。
加速無處不在
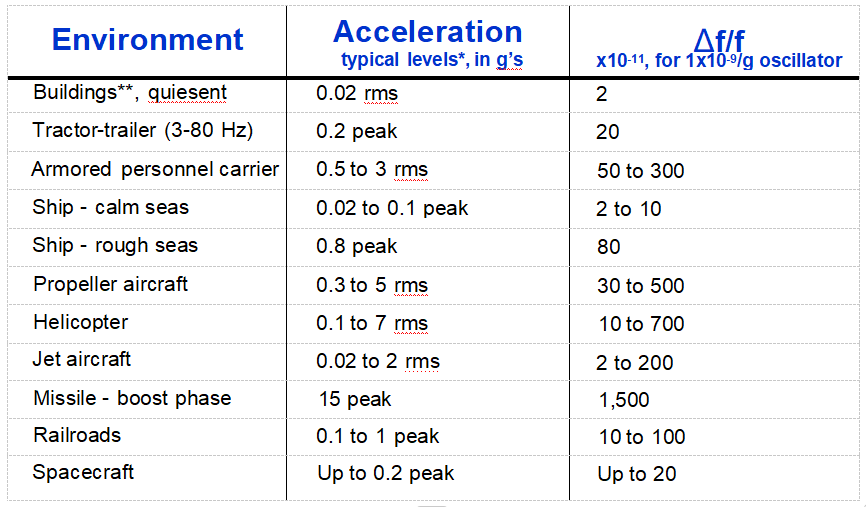
*振蕩器的水平取決于振蕩器的安裝方式和位置。平臺共振可以大大放大加速度水平。
**建筑物振動會對噪聲測量產生重大影響
加速影響“一切”
?加速力變形(應變)
材料和器件特性的變化——在某種程度上
?示例:
-石英諧振器頻率
-放大器增益(應變改變半導體帶結構)
-激光二極管發射頻率
-光學性能.光纖折射率(聲光)
-腔頻率
-DRO頻率(應變改變介電常數)
-原子鐘頻率
-雜散電抗
-時鐘速率(相對論效應)
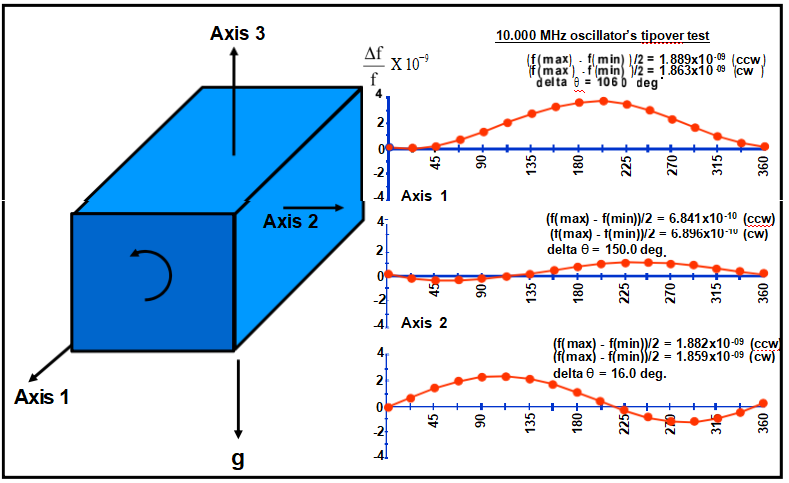
2-g傾翻試驗
(Δf與繞三個軸的姿態)
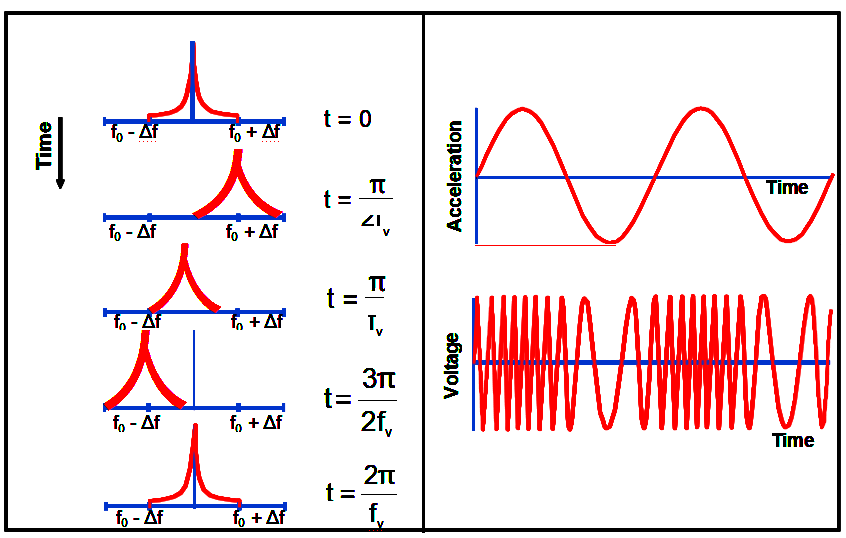
正弦振動調制頻率
加速度靈敏度矢量
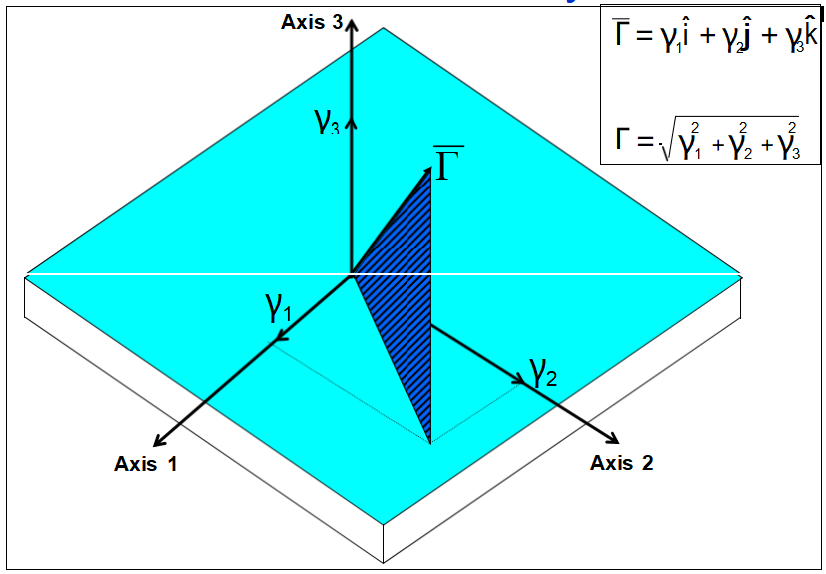
振動引起的艾倫偏差退化
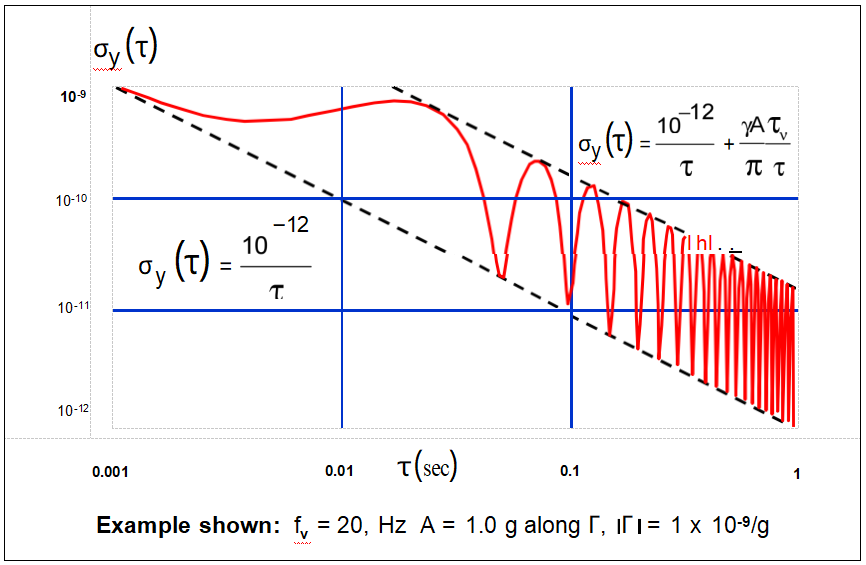
振動引起的相位偏移
振動調制信號的相位為
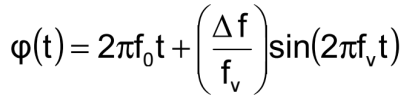
當振蕩器受到正弦振動時,峰值相位偏移為
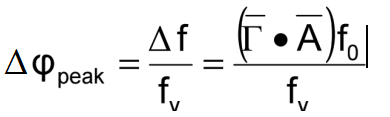
示例:如果10 MHz,1 x 10-9/g振蕩器受到10 Hz的影響
振幅為1g的正弦振動,峰值振動引起的相位偏移為1×10-3弧度。如果將此振蕩器用作參考
10GHz雷達系統中的振蕩器,10GHz處的峰值相位偏移將為1弧度。如此大的相位偏移可能是災難性的
例如采用鎖相環(PLL)或相移鍵控(PSK)的那些系統的性能。
振動引起的邊帶
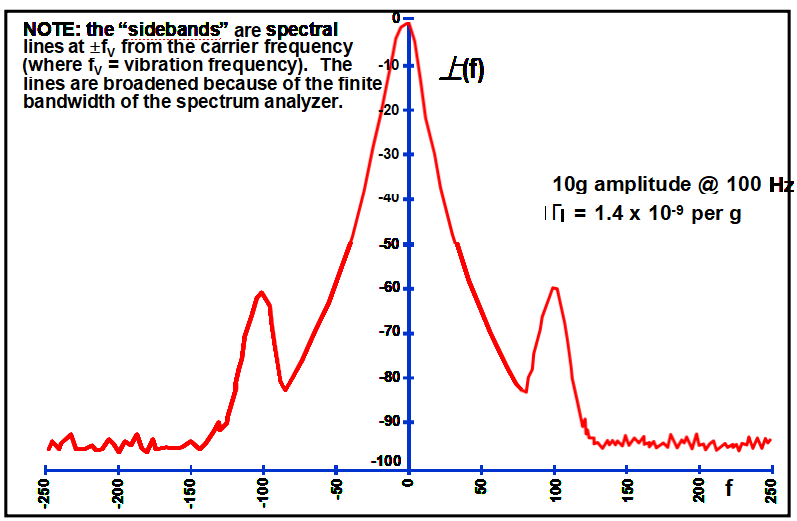
倍頻后振動引起的邊帶
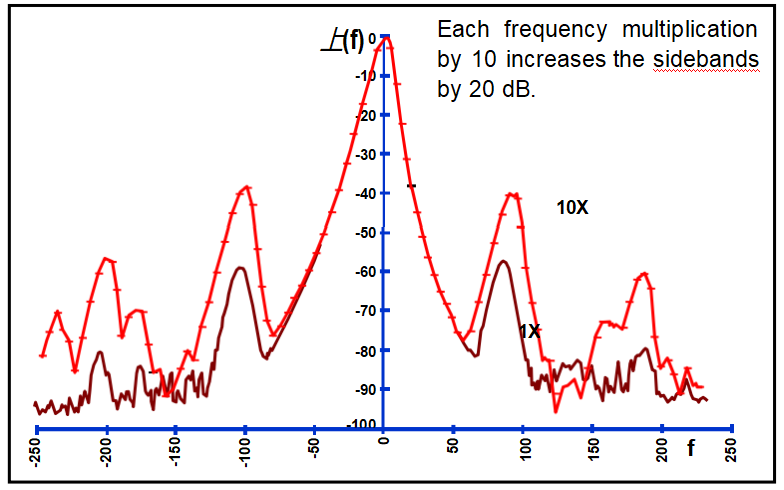
-
振蕩器
+關注
關注
28文章
3832瀏覽量
139136 -
石英晶體
+關注
關注
0文章
171瀏覽量
38569 -
頻率控制
+關注
關注
0文章
23瀏覽量
10020 -
石英晶體諧振器
+關注
關注
0文章
24瀏覽量
2799
發布評論請先 登錄
相關推薦




 石英晶體諧振器和振蕩器 頻率控制和定時應用教程(之四)
石英晶體諧振器和振蕩器 頻率控制和定時應用教程(之四)










評論