引言：

本欄目旨在和大家分享電子設計中的各種技巧。這里是DSP、Electronic、Embedded以及FPGA共同構成的“四維世界”。這里沒有長篇大論，助你“修煉成仙”的功法，只有一針見血，將問題“斬于馬下”的“秘技”。這里面的“秘技”雖說不能獨步天下，但足以給各位大俠的“修煉之路”提供借鑒。

簡介

在許多應用中信號在頻域中檢測或處理比在時域中有優勢。有時優勢就只是一個比較簡單或概念直白的算法，但頻域最大的難點往往是包含在快速傅里葉變換中的復雜度或延遲。如果在一個實時應用中頻域數據經常更新，FFT的復雜性和延遲會成為實現系統目標和保持低成本、低功耗的一個主要障礙。許多現實應用，比如醫學成像、雷達、觸屏感應以及通信系統，都使用頻域算法來檢測和處理信號。在許多實現中復雜性或功耗必須要低，同時要最小化延遲，在上述方面滑動DFT比FFT的頻域計算性能更好。

數學理論基礎

滑動DFT的推導是相當簡單的，并且和DFT完全等價。也就是說，滑動DFT算法相比傳統DFT或FFT算法沒有信息丟失或失真。下面有完整的推導過程，沒有興趣的讀者可以跳過這一節，因為它容易讓人想睡覺。使用滑動DFT的基本前提是很長一段時域數據流在一個長度為N的比較短的轉換窗口里。以一幅頻譜圖為例，頻譜圖是對很長一段或連續的時域采樣數據流按照一定的間隔實施到長度為N的窗口的頻域轉換。

對于滑動DFT的推導，我們首先假設變換使用的是非常新的時域采樣，這樣的話一個長度為N的變換窗口將保持與時域數據流的每一次采樣同步。輸入采樣流用Xk表示，（其中k的范圍比N要廣）在每個K采樣輸入時都能實現長度為N的變換。按照DFT的傳統定義我們可以得到下面的第K個采樣的變換，其中f表示頻率，n表示長度為N的窗口中的標度：

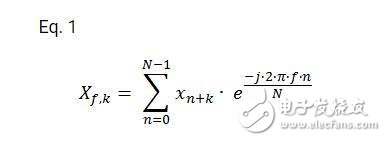
滑動序列的下一次變換是第K+1個采樣，可以表示為：

下一步我們要做的是設p=n+1，用p代替等式二中的n+1，這樣p的范圍就是從1到n，而不是0到n-1。接下來計算和前面是一樣的，只是下標的范圍發生了變化。

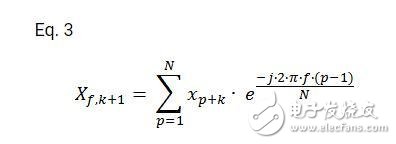
第N個式子可以從總和中獨立出來表示。同時引入p=0的式子，只要在最后減去。這樣看上去雖然很不優美，但是很有用：

上式可以被表示成：

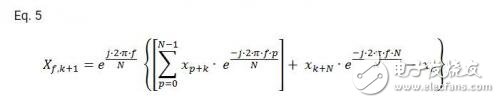
在等式5中，由于f是整數值，所以Xk+N項的指數的值有且只有可能是1+j0，所以此項的值可化簡為Xk+N。
而方括號中的和式正是第K個采樣值的DFT，只是下標由n變為p。因此，等式5可以表示為：

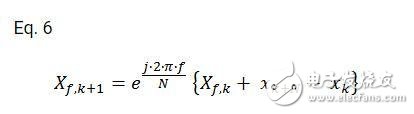
算法實現

等式6就是推導后得出的滑動DFT的表達式。第K+1變換的頻域值Xf,k+1可以從第k個變換的頻域值Xf,k遞歸計算而來。第K+1個采樣的頻域值可以用前一個采樣（第K個）的頻域值加上最新輸入的時域采樣值中的Xk+N與第K個采樣值中的Xk的差，再乘以就可以得到最新的輸出。

相比于使用FFT，滑動DFT的優勢是非常明顯的。滑動DFT避免了很多不必要的運算，降低計算復雜性，節省了很多的計算資源，從而降低功耗。圖1表示了實現等式6的信號流程圖，它的初始延遲和相加是所有計算共用的，復數遞歸乘法以及累加在每個頻率值計算的時候被重復。

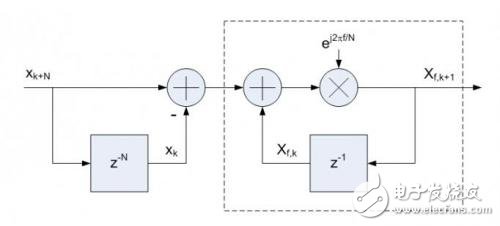
圖1 等式6的信號流程圖

滑動DFT的另一個優點是如果不需要對每個輸入采樣進行變換的話，它可減少不必要的計算。例如，一個變換只需要M個采樣輸入，當所有的計算完成時，滑動DFT的計算復雜性是N×M，而FFT完成相同的工作的計算復雜性卻是N×log2(N)。

初始化

滑動DFT算法的遞歸性意味著需要一些初始化方法。要想輸出的Xf,k+1有效，那么Xf,k也必須是有效的。且每個輸出依賴于前N采樣輸入。有兩種常用的算法初始化方法：

1、在循環采樣數據之前，先使用0來刷新延遲線。類似地，如果緩沖寄存器復位，在循環數據之前，要重置信號路徑存儲器為0，完成刷新。當N個數據采樣完成循環，輸出是有效的。

2、第一種方法中N個循環的初始化延遲可以通過前N個輸入采樣的FFT初始化Xf,k來避免。在一些系統中，特別是離線應用，這個方法很有優勢。