計(jì)數(shù)排序
學(xué)習(xí)基數(shù)排序之前首先學(xué)習(xí)計(jì)數(shù)排序。
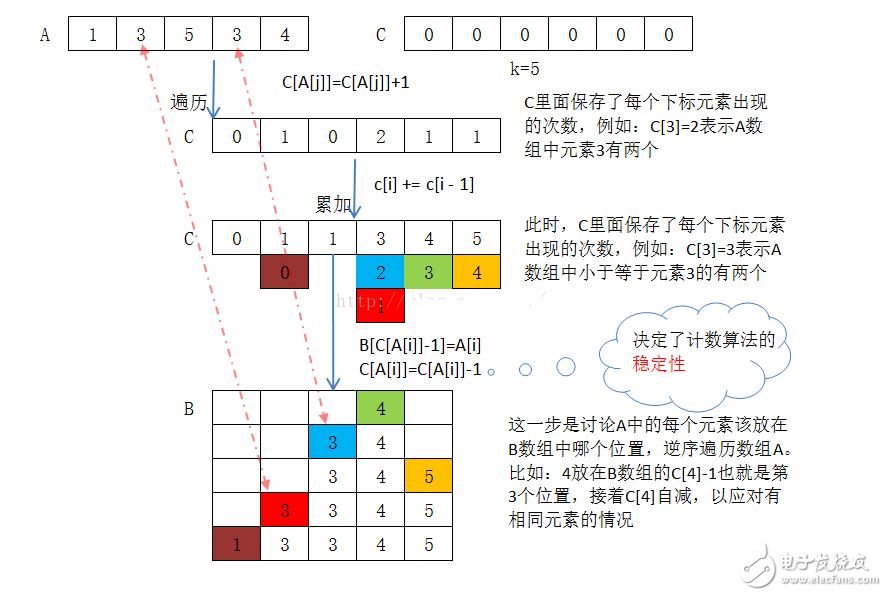
計(jì)數(shù)排序假設(shè)每個(gè)元素都是在0到k之間的一個(gè)整數(shù)。
基數(shù)排序的基本思想,對(duì)于每個(gè)元素x,如果我們知道了小于x的元素的個(gè)數(shù),就可以確定輸出數(shù)組中元素x的位置,那么直接將元素x放到輸出數(shù)組中。比如有3小于x的元素,那在輸出數(shù)組中,x肯定位于第4個(gè)位置。
計(jì)數(shù)排序的算法用偽代碼描述為:
// 初始化數(shù)組C
for i=0 to k
C[i]=0
// 統(tǒng)計(jì)A[j]元素出現(xiàn)的次數(shù),保存到C數(shù)組中
for j=0 to A.length
C[A[j]]=C[A[j]]+1
// 統(tǒng)計(jì)小于等于A[j]元素的個(gè)數(shù)
for k=0 to k
C[K]=C[K-1]+C[K]
// 將A中的元素放在B中正確的位置
for i=A.length to 0
B[C[A[i]]-1]=A[i]
C[A[i]]=C[A[i]]-1
注:由于有可能有相同元素存在,所以,每次將A[i]元素放入B數(shù)組中,都要將C[A[j]]的值減一,這樣當(dāng)遇到下一個(gè)值等于A[j]的元素時(shí),該元素就能放在輸出數(shù)組中A[j]的前面。
計(jì)數(shù)排序的詳細(xì)過(guò)程如下
計(jì)數(shù)排序的關(guān)鍵代碼如下
public int[] countSort(int a[], int k) {
int[] b = new int[a.length];
int[] c = new int[k];
for (int i = 0; i
c[i] = 0;
}
for (int i = 0; i
c[a[i]] += 1;
}
for (int i = 0; i
if (i != 0) {
c[i] += c[i - 1];
}
}
for (int i = a.length - 1; i >= 0; i--) {
b[c[a[i]] - 1] = a[i];
c[a[i]] = c[a[i]] - 1;
}
return b;
}
計(jì)數(shù)排序的性能
很容易得到計(jì)數(shù)排序的時(shí)間復(fù)雜度為:T(n)=O(k+n),因此當(dāng)k小于等于n,也就是當(dāng)k=O(n),k和n同階時(shí),采用計(jì)數(shù)排序的時(shí)間復(fù)雜度為T(mén)(n)=O(n)
同時(shí),計(jì)數(shù)排序也是一種穩(wěn)定的排序算法。
基數(shù)排序最初是用在打孔卡片制表機(jī)上的一種排序算法,由Herman Hollerith發(fā)明,也就是IBM的創(chuàng)始人。
基數(shù)排序從最低為開(kāi)始來(lái)排序的,從低位到高位,按位排序,按位排序必須是穩(wěn)定的。
基數(shù)排序的詳細(xì)過(guò)程
基數(shù)排序算法描述為
RADIX-SORT(A,d)
for i=1 to d
use a stable sort to sort arrat A on digit i
在這里我們選擇計(jì)數(shù)排序。考慮常規(guī)情況,對(duì)[0.。.9]之間的數(shù)排序,k=10,且一般有k<
基數(shù)排序的關(guān)鍵代碼,這里以數(shù)組排序時(shí)按照十進(jìn)制每位進(jìn)行比較。
/**
* 基數(shù)排序
* @param result 最終已排序的數(shù)組,共用一個(gè)節(jié)省空間
* @param maxLen 待排序的數(shù)組中最大的位數(shù)
*/
public static void radixSort(int[] a,int[] result, int maxLen) {
int flag = 1;
// 保存每輪要排序的位對(duì)應(yīng)數(shù)組a的值
int [] digitArr = new int[a.length];
for(int i=0; i
// 共比較的輪數(shù)
flag *= 10;
// b數(shù)組中對(duì)應(yīng)的裝著a數(shù)組中每位的數(shù),第一輪裝著各位,第二輪裝著十位數(shù)。。.
for (int j = 0; j < digitArr.length; j++) {
digitArr[j]=a[j]%flag;
digitArr[j]=digitArr[j]/(flag/10);
}
countSort(a, digitArr,result,10);
// 每一輪計(jì)數(shù)排序完后刷新下一輪要排序的數(shù)組
System.arraycopy(result, 0, a, 0,result.length);
}
}
調(diào)用計(jì)數(shù)排序的函數(shù)
/**
* 計(jì)數(shù)排序 :對(duì)數(shù)組a中的元素按某些位排序
* @param tmp 要參與排序的當(dāng)前位的值保存在tmp中
* @param result 每次計(jì)數(shù)排序后的新的數(shù)組順序
*/
public static void countSort(int a[], int tmp[], int result[], int k) {
int[] c = new int[k];
for (int i = 0; i < c.length; i++) {
c[i] = 0;
}
for (int i = 0; i
c[tmp[i]] += 1;
}
for (int i = 0; i < c.length; i++) {
if (i != 0) {
c[i] += c[i - 1];
}
}
for (int i = tmp.length - 1; i >= 0; i--) {
// 和計(jì)數(shù)排序唯一的差別在于賦值的時(shí)候用真實(shí)的數(shù)據(jù)
result[c[tmp[i]] - 1] = a[i];
c[tmp[i]] = c[tmp[i]] - 1;
}
}
基數(shù)排序的性能
如果基數(shù)排序使用的穩(wěn)定排序算法的時(shí)間復(fù)雜度為O(n+k),那么基數(shù)排序的時(shí)間復(fù)雜度為T(mén)(n)=O(d(n+k))
很容易理解要循環(huán)d輪,每輪耗時(shí)為O(n+k),于是總的耗時(shí)為O(d(n+k))
在此基礎(chǔ)上,從2^r進(jìn)制來(lái)看,此時(shí)k為2^r,并且一個(gè)b位數(shù)要比較b/r輪。于是我們得到T(n)=O((b/r)(n+2^r))
對(duì)上式求導(dǎo)可得其最小值。此時(shí)r=lgn,此時(shí)T(n)=O((b/lgn)n),如果再取b=lgn,這時(shí)就能達(dá)到最少的運(yùn)行時(shí)間,時(shí)間復(fù)雜度為T(mén)(n)=O(n)
基數(shù)排序也是穩(wěn)定的排序算法
基數(shù)排序
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
在TMS320C62x上實(shí)現(xiàn)的擴(kuò)展精度基數(shù)-4快速傅里葉變換

時(shí)間復(fù)雜度為 O(n^2) 的排序算法

OPSL 優(yōu)勢(shì)4:良好的可靠性 - 龐大的安裝基數(shù)
手把手教你排序算法怎么寫(xiě)

具有先進(jìn)排序和輸出裕度的中輸入同步降壓控制器TPS40101數(shù)據(jù)表

具有先進(jìn)排序和輸出裕度的中輸入同步降壓控制器TPS40100數(shù)據(jù)表

3-A、3.3/5V輸入、可調(diào)開(kāi)關(guān)穩(wěn)壓器,具有自動(dòng)跟蹤TM排序功能PTH04000W數(shù)據(jù)表

Linux的sort命令介紹
支持 ACPI 的 10 軌電源排序器和監(jiān)視器UCD9090A數(shù)據(jù)表

FPGA實(shí)現(xiàn)雙調(diào)排序算法的探索與實(shí)踐

想聽(tīng)聽(tīng)48和大對(duì)數(shù)光纜的排序?
PLC中常用進(jìn)制之間是如何轉(zhuǎn)換的?

C語(yǔ)言實(shí)現(xiàn)經(jīng)典排序算法概覽





 基數(shù)排序是怎么排的_基數(shù)排序詳細(xì)過(guò)程
基數(shù)排序是怎么排的_基數(shù)排序詳細(xì)過(guò)程











評(píng)論