作者梅根·O·摩爾 (MeganO. Moore)，弗吉尼亞理工學院暨州立大學

作為基礎設施的重要組成部分，全球定位系統 (GPS) 提供定位、導航和定時 (PNT) 信息，這些信息對于應急響應、測量和建筑以及農業等眾多行業至關重要。鑒于其廣泛的使用和重要性，人們越來越擔心該系統容易受到干擾、欺騙和其他威脅，美國運輸部也因此出臺立法，要求為 GPS 服務提供補充和備份。

在中地球軌道 (MEO) 部署衛星（無論是升級 GPS 還是建立新的衛星星座）的成本高昂，導致人們對使用現有機會信號的興趣日益濃厚。這些信號不是為 PNT 設計的，但可以用于僅有多普勒定位的情況，這只需要有關衛星軌道和傳輸頻率的公開信息。隨著 Starlink 和 OneWeb 等大型低地球軌道 (LEO) 星座的發射，僅使用多普勒定位作為 GPS 備份的可行性增加了。不僅有更多可用的機會信號，而且這些信號的路徑損耗更低，因為衛星距離地球更近，而且低地球軌道衛星的速度更快，從而導致多普勒頻移更大、更容易測量。

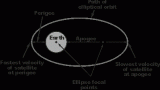
低地球軌道星座在僅多普勒定位和導航方面的潛在用途是一個活躍的研究領域。近日，弗吉尼亞理工大學的研究員 Mark Psiaki 博士發表了一篇論文，表明當同一星座的八顆衛星同時出現時，可以達到與 GPS 相當的精度水平。然而，隨著當前低地球軌道衛星的部署，需要八顆可見衛星，這限制了這種方法在實踐中的實用性。我和弗吉尼亞理工大學國家安全研究所的 William “Chris” Headley 博士、Wireless@VT 的 Michael Buehrer 博士正在合作探索通過隨時間對每顆衛星進行多次測量，以時間分集代替空間分集，以更少的衛星進行操作的可能性（圖 1）。最近，我們證明了使用 MATLAB 和 Satellite Communications Toolbox 這種方法的可行性。我們不僅表明，幾乎從地球上的任何地方都可以看到平均至少五顆衛星，而且四顆衛星實現的空間多樣性與八顆衛星相當。

了解 GDOP 和 D-GDOP

為了分析 GPS 誤差，研究人員開發了一種稱為幾何精度稀釋 (GDOP) 的度量標準。GDOP 量化了衛星相對于接收器的幾何排列，較低的 GDOP 值表示幾何配置更好，因此定位精度更高。例如，如果將一顆 GPS 衛星放置在正上方，將另外三顆衛星放置在地平線上，則其 GDOP 測量值會相對較低，而如果將四顆衛星聚集在同一區域，則其 GDOP 測量值會較高，因此定位精度會較低。

一種稱為 D-GDOP 的類似概念已經為多普勒定位而開發。與 GPS 使用的傳統 GDOP 公式不同，D-GDOP 考慮了視野中衛星的速度和加速度。因此，最小化 GDOP 的衛星幾何形狀不一定會使 D-GDOP 最小化，反之亦然。更進一步來說，時間多樣化的 D-GDOP，或者 D-GDOPT，是相同的概念，但應用于一種方法，其中對每個衛星的多普勒測量是隨著時間的推移而不是一次性進行的。在我們的研究中，我們想看看 D-GDOPT 的衡量標準（例如，使用四顆衛星）與使用八顆衛星的 D-GDOP 測量值進行比較——這將使我們能夠確定時間分集是否可以作為空間分集的充分替代品。然而，首先我們需要驗證，對于給定的低地球軌道 (LEO) 星座而言，預期至少有四顆衛星進入視野是合理的。

分析衛星可用性

在評估衛星可見性時，首先要考慮的因素之一是衛星的地平線以上高度。以 GPS 為例，通常使用 10 度的遮蓋高度 - 任何高于該高度的衛星都被視為可見，忽略障礙物造成的潛在阻擋。對于低地球軌道衛星的分析，我們需要應用類似的掩模，但要考慮到這些衛星用于通信的光束，這些光束比 GPS 衛星使用的光束要窄得多。根據技術文檔和向聯邦通信委員會 (FCC) 提交的文件，我們將 OneWeb 衛星的仰角設置為 25 度，將 Starlink 衛星的仰角設置為 40 度。在低于這些掩模的高度，來自衛星的信號可能太弱而無法可靠地使用。

接下來，我們需要確定從地球的各個位置可以看到哪些衛星。為了評估全球范圍內的可用性，我們使用來自 Starlink 和 OneWeb 衛星的真實軌道數據，檢查了全球每 10 度緯度和 60 度經度的可見性。具體來說，我們使用了從 CelesTrak 下載的這些星座的雙線元素 (TLE) 數據。

利用 MATLAB 和Satellite Communications Toolbox，我們創建了一個衛星場景，以根據下載的數據對軌道衛星進行建模和可視化。我們使用 satelllite 函數讀取和解析基于文本的 TLE 文件以獲得完整的軌道——Starlink 大約需要 95 分鐘，OneWeb 大約需要 110 分鐘。我們幾乎立即就能在衛星場景查看器中看到衛星軌道。這個 link 函數使我們能夠執行鏈路分析，以確定在地面上，特定接收器可以使用每顆衛星信號的時間間隔。

然后，我們編寫了一個 MATLAB 腳本，循環遍歷所有緯度和經度組合（分別以 10 度和 60 度為增量），并計算每個位置視野范圍內的平均衛星數量（圖 2）。分析顯示，在所有檢查地點，平均可見至少五顆衛星，而在一些距離赤道較遠的地區，可見衛星數量則更多。

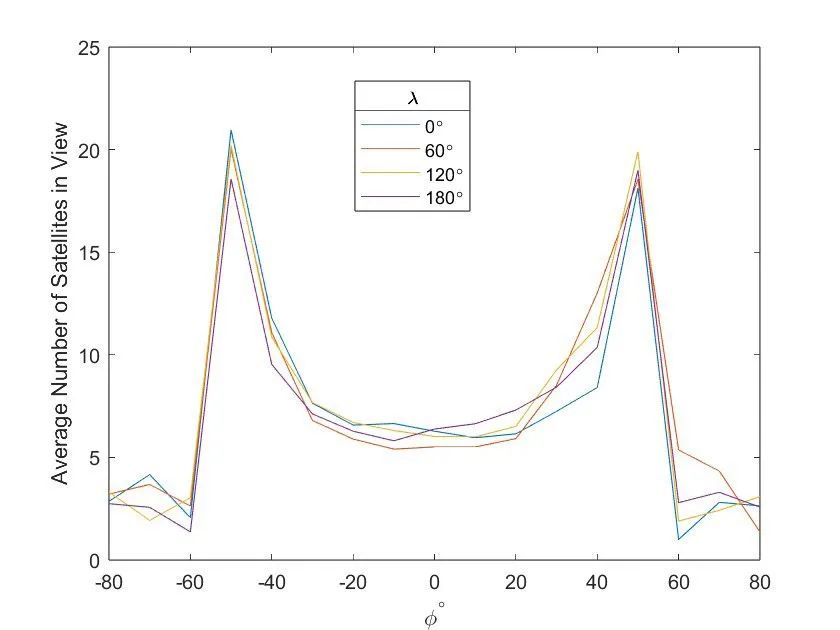
圖 2. OneWeb 星座（上圖）和Starlink 星座（下圖）在不同緯度的衛星可見性。在赤道附近的緯度地區，可見的衛星通常較少，因為赤道上一度經度所覆蓋的距離大約是緯度 60 度上一度經度所覆蓋的距離的兩倍。

評估時間多樣化的 D-GDOP

一旦我們確定，平均而言，單個星座中的五顆或更多顆 LEO 衛星可能從任何位置都可見，下一步就是計算時間差異的 D-GDOP 指標，并將其與使用八顆衛星計算的傳統 D-GDOP 指標進行比較。盡管理論上可以使用一顆衛星在八個不同時間進行多普勒測量，但實際上這會產生極高的 D-GDOPT 因為計算中使用的速度矢量缺乏多樣性。根據我們對衛星可見性的分析，我們選擇使用四顆衛星——每顆衛星在兩個不同的時間進行測量。此外，由于我們事先不知道測量之間的最佳時間間隔（Δt）將是，我們考慮了 Δt 從 1 秒到 101 秒，以 1 秒為增量。（當時間超過 101 秒時，部分或全部衛星可能已經移出視野。）

為了進行比較，我們考慮了恰好有八顆衛星可見的場景，以便可以計算傳統的 D-GDOP。我們編寫了一個 MATLAB 腳本來計算當佛羅里達州卡納維拉爾角可以看到八顆衛星時單個軌道內所有時間的D-GDOP。然后，我們為每個星座挑選出 D-GDOP 最高和最低的場景，然后針對每種情況計算 D-GDOPT，使用 8 顆衛星中 4顆衛星的所有 70 種可能組合（假設Δt = 1)。最后，選擇出導致 D-GDOPT 最高值和最低值的組合我們編寫了一個 MATLAB 腳本來自動計算 D-GDOPT 對于所選的四顆衛星組合在 100 秒范圍內 Δt。最低的 D-GDOPT表 1 顯示了四種場景下達到的值，以及兩個星座的最佳和最壞情況的 D-GDOP 值。總體而言，D-GDOPT措施明顯優于最壞情況的 D-GDOP 情景，并且與最佳情況的 D-GDOP 情景相當。

表 1. 最小 D-GDOPT 最佳和最差四衛星組合的值，與相應的八衛星組合的 D-GDOP 值相比。

在我們進行分析時，我們遇到了一些異常大的 D-GDOP 值，例如針對最壞情況的 OneWeb 場景計算出的 3,746 值。在早期的研究中，由于沒有考慮更高的海拔掩模，D-GDOP 分析得出的值要小得多。事實上，我們的分析顯示的一些較大的 D-GDOP 值與其他研究人員得出的較小值之間的巨大差異最初讓我們停下來思考，隨后凸顯了使用 Satellite Communications Toolbox 的優勢之一。如果我們編寫了自己的軌道傳播程序來獲得 D-GDOP 計算所需的衛星速度和加速度，如此大的差異會讓我們質疑我們的實施。在這種情況下，由于我們使用了經過驗證的工具箱功能，我們對結果充滿信心，并節省了數小時的編程時間和代碼審查時間。

作為分析的一部分，我們還仔細研究了 Δt 如何影響 D-GDOPT。我們發現如果 Δt 值較高，D-GDOPT 有時會增加，在某些情況下，最差的組合可能會開始超越最好的衛星組合Δt = 1（圖 3）。造成這一現象的原因很復雜。一方面，隨著 Δt 的增加，衛星離其初始位置越來越遠，從而增加了空間多樣性。另一方面，它還改變了衛星相對于地面接收器的速度。需要更好地理解 D-GDOP 計算中位置、速度和加速度矢量之間的相互作用，以找到最佳值 Δt，這是進一步研究的可能途徑之一。

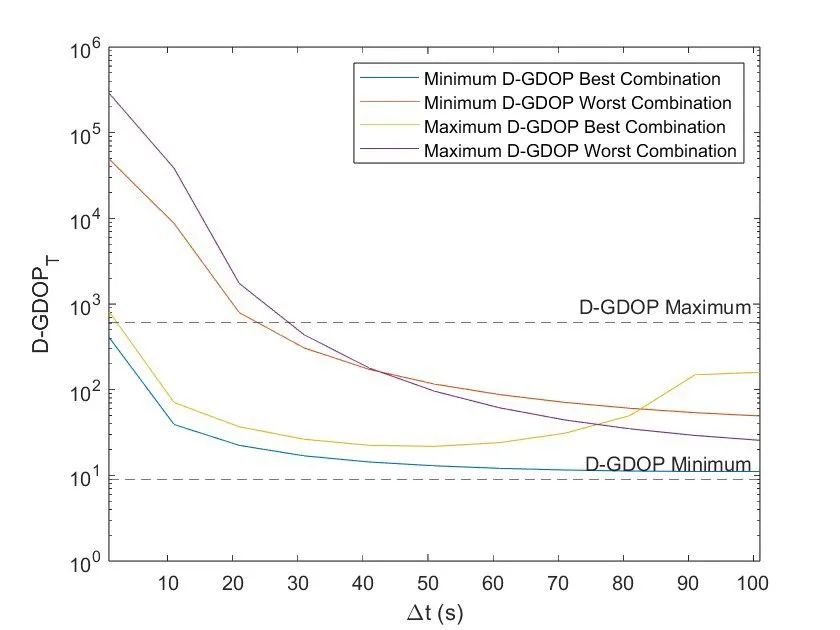
圖 3. 在 Δt 范圍內D-GDOP T的值的圖。

后續步驟

事實證明，當可用的低地球軌道衛星少于八顆時，僅使用多普勒定位是可行的，我們的研究重點正在向多個方向擴展。首先，我們最初的研究僅考慮了固定用戶。對于行人來說，用戶速度對我們的計算的影響可能很小，但對于飛機和其他高速車輛，我們必須考慮到用戶的位置可能會發生很大變化，因為 Δt 增加。

俄亥俄州立大學的 Zak Kassas 博士探索了使用多個星座的衛星，例如結合 OneWeb、Starlink 和Iridium 衛星的測量結果。進一步的研究可能涉及將他的方法與時間多樣化方法相結合以進一步提高可用性。此外，我們計劃更深入地研究 D-GDOP 最小化策略，可能使用 Global OptimizationToolbox。我們下一步最重要的工作是開發一個完整的模型，該模型能夠根據來自少于八顆低地球軌道 (LEO) 衛星的時間差異多普勒測量來確定位置。