K-MEANS算法

K-MEANS算法是輸入聚類個數k，以及包含 n個數據對象的數據庫，輸出滿足方差最小標準k個聚類的一種算法。k-means 算法接受輸入量 k ；然后將n個數據對象劃分為 k個聚類以便使得所獲得的聚類滿足：同一聚類中的對象相似度較高；而不同聚類中的對象相似度較小。

聚類相似度是利用各聚類中對象的均值所獲得一個“中心對象”（引力中心）來進行計算的。

K-Means聚類算法原理

K-Means算法是無監督的聚類算法，它實現起來比較簡單，聚類效果也不錯，因此應用很廣泛。K-Means算法有大量的變體，本文就從最傳統的K-Means算法講起，在其基礎上講述K-Means的優化變體方法。包括初始化優化K-Means++， 距離計算優化elkan K-Means算法和大數據情況下的優化Mini Batch K-Means算法。

1. K-Means原理初探

K-Means算法的思想很簡單，對于給定的樣本集，按照樣本之間的距離大小，將樣本集劃分為K個簇。讓簇內的點盡量緊密的連在一起，而讓簇間的距離盡量的大。

如果用數據表達式表示，假設簇劃分之間的隨機數為（C1，C2，。。.Ck），則我們的目標是最小化平方誤差E：

E=∑i=1k∑x∈Ci||x?μi||22E=∑i=1k∑x∈Ci||x?μi||22

其中μi是簇Ci的均值向量，有時也稱為質心，表達式為：

μi=1|Ci|∑x∈Cixμi=1|Ci|∑x∈Cix

如果我們想直接求上式的最小值并不容易，這是一個NP難的問題，因此只能采用啟發式的迭代方法。K-Means采用的啟發式方式很簡單，用下面一組圖就可以形象的描述。

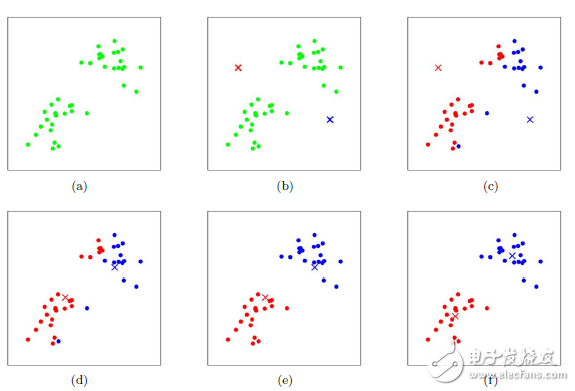
上圖a表達了初始的數據集，假設k=2。在圖b中，我們隨機選擇了兩個k類所對應的類別質心，即圖中的紅色質心和藍色質心，然后分別求樣本中所有點到這兩個質心的距離，并標記每個樣本的類別為和該樣本距離最小的質心的類別，如圖c所示，經過計算樣本和紅色質心和藍色質心的距離，我們得到了所有樣本點的第一輪迭代后的類別。此時我們對我們當前標記為紅色和藍色的點分別求其新的質心，如圖4所示，新的紅色質心和藍色質心的位置已經發生了變動。圖e和圖f重復了我們在圖c和圖d的過程，即將所有點的類別標記為距離最近的質心的類別并求新的質心。最終我們得到的兩個類別如圖f。當然在實際K-Mean算法中，我們一般會多次運行圖c和圖d，才能達到最終的比較優的類別。

讀者可以通過下面這個動態圖來形象的了解算法的實現過程

在上一節我們對K-Means的原理做了初步的探討，這里我們對K-Means的算法做一個總結。

首先我們看看K-Means算法的一些要點。

1）對于K-Means算法，首先要注意的是k值的選擇，一般來說，我們會根據對數據的先驗經驗選擇一個合適的k值，如果沒有什么先驗知識，則可以通過交叉驗證選擇一個合適的k值。

2）在確定了k的個數后，我們需要選擇k個初始化的質心，就像上圖b中的隨機質心。由于我們是啟發式方法，k個初始化的質心的位置選擇對最后的聚類結果和運行時間都有很大的影響，因此需要選擇合適的k個質心，最好這些質心不能太近。

好了，現在我們來總結下傳統的K-Means算法流程。

輸入是樣本集D={x1，x2，。..xm}D={x1，x2，。..xm}，聚類的簇樹k，最大迭代次數N

輸出是簇劃分C={C1，C2，。..Ck}C={C1，C2，。..Ck}

1） 從數據集D中隨機選擇k個樣本作為初始的k個質心向量： {μ1，μ2，。..，μk}{μ1，μ2，。..，μk}

2）對于n=1，2，。..，N

a） 將簇劃分C初始化為Ct=?t=1，2.。.kCt=?t=1，2.。.k

b） 對于i=1，2.。.m，計算樣本xixi和各個質心向量μj（j=1，2，。..k）μj（j=1，2，。..k）的距離：dij=||xi?μj||22dij=||xi?μj||22，將xixi標記最小的為dijdij所對應的類別λiλi。此時更新Cλi=Cλi∪{xi}Cλi=Cλi∪{xi}

c） 對于j=1，2，。..，k，對CjCj中所有的樣本點重新計算新的質心μj=1|Cj|∑x∈Cjxμj=1|Cj|∑x∈Cjx

e） 如果所有的k個質心向量都沒有發生變化，則轉到步驟3）

3） 輸出簇劃分C={C1，C2，。..Ck}C={C1，C2，。..Ck}

3. K-Means初始化優化K-Means++

在上節我們提到，k個初始化的質心的位置選擇對最后的聚類結果和運行時間都有很大的影響，因此需要選擇合適的k個質心。如果僅僅是完全隨機的選擇，有可能導致算法收斂很慢。K-Means++算法就是對K-Means隨機初始化質心的方法的優化。

關于這里，原作者博客寫的有點兒含糊，網上有幾篇博客寫的不是很清楚，這里把他們總結在一起，特別對有問題的地方用紅色字體解釋和說明：

k-means++算法選擇初始seeds的基本思想就是：初始的聚類中心之間的相互距離要盡可能的遠。wiki上對該算法的描述是如下：

1，從輸入的數據點集合中隨機選擇一個點作為第一個聚類中心

2，對于數據集中的每一個點x，計算它與最近聚類中心（指已選擇的聚類中心）的距離D（x）

3，選擇一個新的數據點作為新的聚類中心，選擇的原則是：D（x）較大的點，被選取作為聚類中心的概率較大

4，重復2和3直到k個聚類中心被選出來

5，利用這k個初始的聚類中心來運行標準的k-means算法

從上面的算法描述上可以看到，算法的關鍵是第3步，如何將D（x）反映到點被選擇的概率上，一種算法如下：

1，先從我們的數據庫隨機挑個隨機點當“種子點”

2，對于每個點，我們都計算其和最近的一個“種子點”的距離D（x）并保存在一個數組里，然后把這些距離加起來得到Sum（D（x））。

3，然后，再取一個隨機值，用權重的方式來取下一個“種子點”。

這個算法的實現是：先取一個能落在Sum（D（x））中的隨機值Random，然后用Random -= D（x），直到，Random《=0（注意，這個式子的意思是：在剛才保存的那個數組里，我們從頭開始遍歷每一個元素的D（x），直到減掉的Random小于0，此時停止），此時的點就是下一個“種子點”。

4，重復2和3直到k個聚類中心被選出來

5，利用這k個初始的聚類中心來運行標準的k-means算法

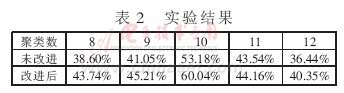
可以看到算法的第三步選取新中心的方法，這樣就能保證距離D（x）較大的點，會被選出來作為聚類中心了。至于為什么原因很簡單，如下圖 所示：

假設A、B、C、D的D（x）如上圖所示，當算法取值Sum（D（x））*random（原作者博客里這樣寫是因為在編程語言中，random函數產生的是0-1之間的 隨機數，所以他用Sum（D（x））*random來表示隨機生成一個位于［0-Sum（D（x））］之間的隨機數），該值會以較大的概率落入D（x）較大的區間內，所以對應的點會以較大的概率被選中作為新的聚類中心。

4. K-Means距離計算優化elkan K-Means

在傳統的K-Means算法中，我們在每輪迭代時，要計算所有的樣本點到所有的質心的距離，這樣會比較的耗時。那么，對于距離的計算有沒有能夠簡化的地方呢？elkan K-Means算法就是從這塊入手加以改進。它的目標是減少不必要的距離的計算。那么哪些距離不需要計算呢？elkan K-Means利用了兩邊之和大于等于第三邊，以及兩邊之差小于第三邊的三角形性質，來減少距離的計算。

第一種規律是對于一個樣本點x和兩個質心μj1，μj2。如果我們預先計算出了這兩個質心之間的距離D（j1，j2），則如果計算發現2D（x，j1）≤D（j1，j2），我們立即就可以知道

D（x，j1）≤D（x，j2）。此時我們不需要再計算D（x，j2），也就是說省了一步距離計算。

第二種規律是對于一個樣本點xx和兩個質心μj1，μj2。我們可以得到D（x，j2）≥max{0，D（x，j1）?D（j1，j2）}這個從三角形的性質也很容易得到。

利用上邊的兩個規律，elkan K-Means比起傳統的K-Means迭代速度有很大的提高。但是如果我們的樣本的特征是稀疏的，有缺失值的話，這個方法就不使用了，此時某些距離無法計算，則不能使用該算法。

5. 大樣本優化Mini Batch K-Means

在傳統的K-Means算法中，要計算所有的樣本點到所有的質心的距離。如果樣本量非常大，比如達到10萬以上，特征有100以上，此時用傳統的K-Means算法非常的耗時，就算加上elkan K-Means優化也依舊。在大數據時代，這樣的場景越來越多。此時Mini Batch K-Means應運而生。

顧名思義，Mini Batch，也就是用樣本集中的一部分的樣本來做傳統的K-Means，這樣可以避免樣本量太大時的計算難題，算法收斂速度大大加快。當然此時的代價就是我們的聚類的精確度也會有一些降低。一般來說這個降低的幅度在可以接受的范圍之內。

在Mini Batch K-Means中，我們會選擇一個合適的批樣本大小batch size，我們僅僅用batch size個樣本來做K-Means聚類。那么這batch size個樣本怎么來的？一般是通過無放回的隨機采樣得到的。

為了增加算法的準確性，我們一般會多跑幾次Mini Batch K-Means算法，用得到不同的隨機采樣集來得到聚類簇，選擇其中最優的聚類簇。

6. K-Means（K-近鄰學習）與KNN（k-近鄰估計）

初學者很容易把K-Means和KNN搞混，兩者其實差別還是很大的。

K-Means是無監督學習的聚類算法，沒有樣本輸出；而KNN是監督學習的分類算法，有對應的類別輸出。KNN基本不需要訓練，對測試集里面的點，只需要找到在訓練集中最近的k個點，用這最近的k個點的類別來決定測試點的類別。而K-Means則有明顯的訓練過程，找到k個類別的最佳質心，從而決定樣本的簇類別。

當然，兩者也有一些相似點，兩個算法都包含一個過程，即找出和某一個點最近的點。兩者都利用了最近鄰（nearest neighbors）的思想。

7. K-Means小結

K-Means是個簡單實用的聚類算法，這里對K-Means的優缺點做一個總結。

K-Means的主要優點有：

1）原理比較簡單，實現也是很容易，收斂速度快。

2）聚類效果較優。

3）算法的可解釋度比較強。

4）主要需要調參的參數僅僅是簇數k。

K-Means的主要缺點有：

1）K值的選取不好把握

2）對于不是凸的數據集比較難收斂

3）如果各隱含類別的數據不平衡，比如各隱含類別的數據量嚴重失衡，或者各隱含類別的方差不同，則聚類效果不佳。

4） 采用迭代方法，得到的結果只是局部最優。

5） 對噪音和異常點比較的敏感。

k-means聚類算法的應用

聚類就是按照一定的標準將事物進行區分和分類的過程，該過程是無監督的，即事先并不知道關于類分的任何知識。聚類分析又稱為數據分割，它是指應用數學的方法研究和處理給定對象的分類，使得每個組內部對象之間的相關性比其他對象之間的相關性高，組間的相異性較高。

聚類算法被用于許多知識領域，這些領域通常要求找出特定數據中的“自然關聯”。自然關聯的定義取決于不同的領域和特定的應用，可以具有多種形式。典型的應用例如：

1. 商務上，幫助市場分析人員從客戶基本資料庫中發現不同的客戶群，并用購買模式來刻畫不同客戶群的特征；

2. 聚類分析是細分市場的有效工具，同時也可用于研究消費者行為，尋找新的潛在市場、選擇實驗的市場，并作為多元分析的預處理。

3. 生物學上，用于推導植物和動物的分類，對基因進行分類，獲得對種群固有結構的認識；

4. 地理信息方面，在地球觀測數據庫中相似區域的確定、汽車保險單持有者的分組，及根據房子的類型、價值和地理位置對一個城市中房屋的分組上可以發揮作用；

5. 聚類也能用于在網上進行文檔歸類來修復信息；

6. 在電子商務網站建設數據挖掘中的應用，通過分組聚類出具有相似瀏覽行為的客戶，并分析客戶的共同特征，可以更好的幫助電子商務的用戶了解自己的客戶，向客戶提供更合適的服務。

7. 聚類分析可以作為其它數據挖掘算法的預處理步驟，便于這些算法在生成的簇上進行處理。