寫在前面的話
文明的進步總是朝著公平、公正、公開的方向。技術的進步總是朝著舒適、便利、快捷的方向。鋼筆讓毛筆走入了歷史;網絡通訊讓惜字如金的電報,洋洋灑灑的書信都走入了歷史。
當一種技術發展到極端的時候,往往另外一種顛覆性的技術就在醞釀中。內燃機驅動的汽車過去一百年來變得更漂亮、更舒適,當然也發展到了極限。比如零到一百公里加速特性在5秒之內;混合工況百公里油耗在5升以內(每公里成本約為0.4元),這兩大分別評價動力性和經濟性的指標對于家用純汽油內燃機常規車輛來說是不可逾越的邊界。即便是達到其中一個指標都需要極高的成本(跑車,超輕汽車)。
作為技術替代品,電動汽車輕而易舉的同時達到了上述目標。電動汽車疊加燃油車永遠不再可能企及的智能駕駛技術引領了汽車進入了新的時代。
工業仿真伴隨著計算技術和計算機硬件的進步,過去六十年取得了突飛猛進的發展。但是工業仿真也存在類似汽車的計算技術極限:尺度跨度不超過6個數量級和計算在秒級完成。這兩個技術極限在目前以微分方程空間時間離散為核心的當前主流求解器框架下是無法同時解決的。
以經典機器學習和深度學習為代表的AI輔助仿真技術打開了突破極限的通路:卷積技術使得人們可以在米級計算尺度上分辨微米級的幾何特征;圖網絡和物理知情網絡使得仿真計算可以在秒級完成。
AI輔助仿真技術方興未艾!
AI輔助有限元仿真
人工智能 (AI) 是近年來受到高度關注的領域之一。人工智能是指模仿人類智能的基于知識的系統,是使用復雜的算法和數學函數構建的,這些算法和數學函數具有人類和理性思考和行動的能力 。由于計算能力和新算法的進步,AI 在過去三十年中經歷了指數級增長。機器學習 (ML) 和深度學習 (DL) 是 AI 的兩個子領域。ML 和 DL越來越多地在各個領域解決一些現實世界的問題,包括科學、工程、醫療保健、金融和經濟、農業以及計算機視覺和自然語言處理。
數據被認為是任何 ML 算法的核心。在輸入到任何 ML 模型之前,會對獲取的數據進行預處理。數據質量評估、檢查任何缺失值、清理(刪除任何異常值)、縮放和轉換都包含在數據預處理中。數據中的相關特征被饋送到 ML 算法。ML 模型經過訓練以了解訓練數據的特征,并使用測試數據評估性能。
在過去的 80 年里,有限元法 (FEM) 已經發展成為計算力學領域著名的偏微分方程求解器 。有限元分析 (FEA) 因其能夠解決各種問題領域而被廣泛使用,包括結構力學、流體流動分析、熱傳導、增材制造、電氣和電子領域、生物工程等。有限元分析的過程是基于將幾何域離散化為更小的子域,稱為單元。在每個元素上,主變量使用插值函數(也稱為形狀函數或基函數)進行近似。每個單元的控制方程是使用直接或變分或加權殘差方法得出的。代數元素方程在解空間中組裝在一起,并針對一級和二級變量求解生成的方程組。
科學和工程問題通常分為三類:(a) 缺乏科學知識的純數據驅動問題;(b) 科學知識有限的問題,需要一定數量的數據來解釋物理定律以提供完整的解決方案;(c) 具有已知控制方程但計算成本太高而無法獲得完整解的問題 [24]。FEA 的求解過程在數學上是密集的,因為它涉及明確的數學規則來描述問題的物理特性。隨著問題的復雜性,這個過程變得更具挑戰性。另一方面,ML 利用尋找新規則來描述任何沒有任何明確規則的現象。根據提供給 ML 算法的數據,它以隱式方式映射輸入和輸出。因此,由于數據驅動方法的發展,有限元 (FE) 社區也在研究 ML 和 DL 的應用,以發現和實現計算力學的新范式。
此外,FEM 和 ML 有自己的特點,突出了它們的優點和缺點。例如,FEM 的數學精度使其無法處理數據中的任何不穩定性和噪聲。FEM 是基于數學的,更適合直接或正向分析。然而,由于缺乏獨特的解,FEA 不太適合于逆向分析。FEA 的輸出可能不包含足夠的信息,無法唯一地確定系統的輸入。
另一方面,機器學習算法,如人工神經網絡 (ANN),能夠在算法通過訓練學習時處理不確定性和噪聲。ANN 的詳細信息將在后面的部分中討論。然而,ANN 是受生物學啟發的,它可以有效地處理非唯一的逆問題。除此之外,人工神經網絡還通過映射訓練數據的輸入輸出來學習。訓練數據僅包含我們感興趣的一系列變量。但是,ANN 可以在提供的訓練數據范圍之外學習該函數。準確性可能會有所不同,或者結果的意義可能會降低,具體取決于與訓練數據集的偏差。這使得 ANN 比 FEM 更健壯。在對 FE 模型進行建模時,需要將誤差收斂為零。但是,在任何 ML 模型的建模中,在模型訓練期間將誤差減少到零是不可取的。如果誤差為零,則 ML 模型將失去其泛化能力,這在 ML 文獻中稱為過擬合問題。
由于其數據驅動的方法,ML 的效用超越了各個領域。在計算力學領域,許多研究人員通過采用 ML 技術顯著推動了該領域的發展,尤其是在計算資源受到限制的時期,早于 DL 的當前時代。已經出現了幾項開創性的工作,體現了 ML 在計算力學中的早期應用。例如,研究人員在本構建模、梁結構的材料參數識別、缺陷識別和裂紋分析方面做出了顯著的貢獻。
近幾十年來,ML 在 FEA 中的應用已被廣泛報道。由于其通用的近似特性,與其他ML算法相比,ANN在各種應用中都表現出了更好的性能。1990 年代初,FEM 中的 ANN 首次付諸實踐。使用神經網絡對泊松方程的能量泛函進行最小化,以解決有限元法中的電場問題和不可壓縮粘性流問題。在有限元元中實現神經網絡的早期研究包括穩態納維-斯托克問題的最佳收斂準則的估計、桁架的結構分析、波傳播模擬、冷平板軋中的速度場和中性點預測、殘余應力預測和彈塑性中變分原理的最小化。
ML的算法
ML 的主要任務可以分為回歸、分類和聚類。基于回歸的 ML 模型適合給定數據集的線性或非線性曲線。基于分類的 ML 模型以監督方式將數據集分類為預定義數量的類。聚類算法以無監督方式對給定的示例集進行分組根據我們的綜述,一些 ML 算法在 FEA 領域得到了廣泛的應用,例如支持向量機 (SVM)、決策樹、隨機森林、k 最近鄰 (KNN)、k-means 聚類、邏輯回歸、ANN、CNN 和遞歸神經網絡 (RNN)。
人工神經網絡 (ANN) 是最常用的 ML 算法之一。ANN 的靈感來自生物神經網絡。神經元是 ANN 的基礎信息處理單元。輸入信號由它們各自的神經元突觸加權,被匯總形成一個線性組合。提供了一個激活函數來限制神經元的輸出,它是輸入的加權和的函數。
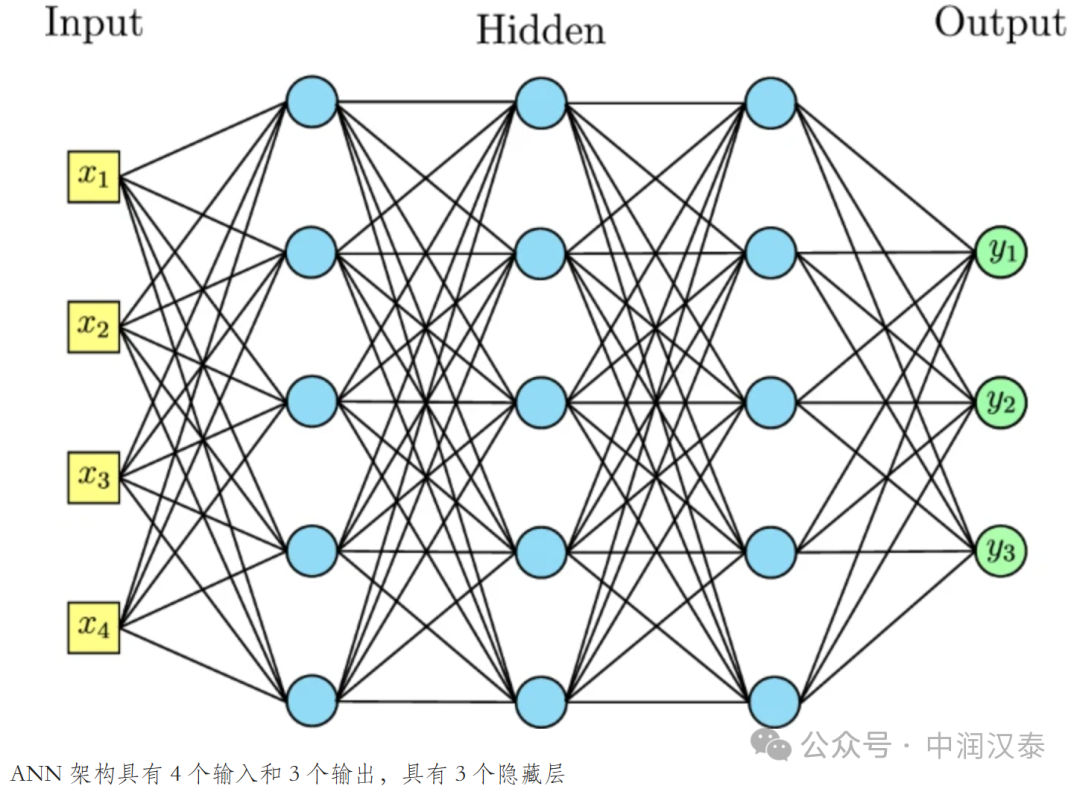
卷積神經網絡(CNN)是一種DL模型,用于處理網格模式的數據,如時間序列數據和圖像。CNN 架構的主要構建塊是卷積層、池化層和全連接層。卷積和池化層從輸入圖像中提取特征。卷積的數學運算是使用多個核濾波器在卷積層中執行的。一個卷積層(稱為特征圖)的輸出被傳遞到下一個層,以提取輸入圖像的其他相關特征。下一層,池化層通過減少特征圖的空間維度,對卷積層的輸出進行下采樣。根據所使用的方法,有幾種類型的池化操作,如樹池化、門控池化、平均池化、最小池化、最大池化、全局平均池化(GAP)和全局最大池化。池化層的扁平化輸出通過全連接層傳遞,該層由可學習參數(即權重和偏差)以及神經元組成,以執行回歸或分類任務。
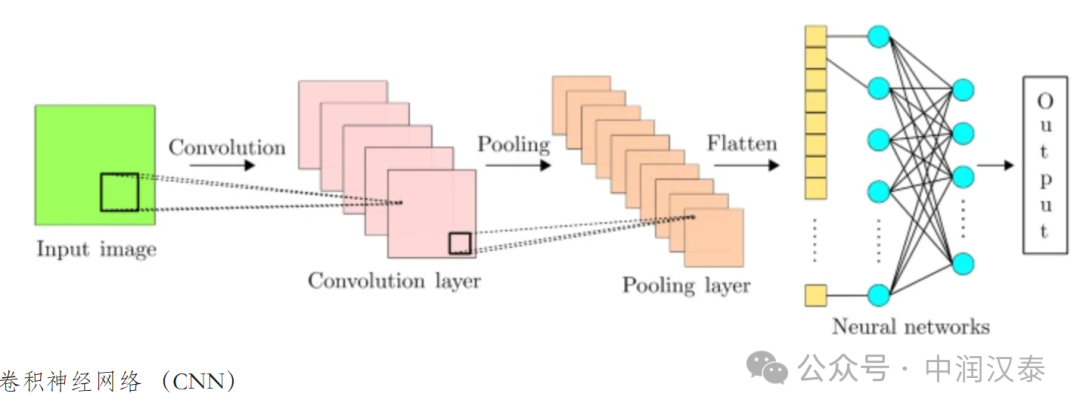
DL 是指神經網絡的深度,即 DL 具有更多數量的隱藏層,使 DL 能夠捕獲數據的復雜行為。ML 模型通常需要特征工程。另一方面,ANN 使 DL 能夠以原始形式處理數據,并自行學習特征。包含噪聲、異常值和異常的大型數據集使特征提取更具挑戰性。雖然 DL 確實是 ML 的一個子集,但根本區別在于它們的學習機制和數據要求。DL 表現出更復雜的學習過程,與更廣泛的 ML 算法類別相比,往往需要更多的數據。ML 模型在處理大型和更高維數據集時面臨困難。這通常會導致降維。ML 通過分解為更小的任務,然后組合結果來解決問題。另一方面,DL 以端到端的方式解決問題。
ML與預處理
預處理是有限元分析三個步驟中的第一步,涉及定義幾何結構、材料屬性、網格、載荷和邊界條件、單元類型和積分參數。幾何結構的準備是 FEM 預處理的關鍵步驟。
眾所周知,有限元解的質量取決于有限元網格的質量。具有足夠細網格的 FEM 模型可以獲得準確的結果,盡管與粗網格相比,計算時間更長。粗網格可能會在較短的時間內給出結果,但精度可能不是最佳的。結構良好的網格可以在更短的計算時間內實現更高的精度。因此,了解是否需要重新劃分網格變得至關重要。為了確保結果的質量可接受,FE 網格需要通過各種質量檢查。這包括檢查一些指標,如縱橫比、偏度、包裹因子、允許的角角、正交度和雅可比矩陣。對于復雜的域和仿真,需要投入大量手動工作來提高網格生成的質量。這些網格需要手動審查,如果需要,通常會執行重新網格劃分。Sprave 和 Drescher開發了兩種基于分類的 ML 模型:基于樹的模型和 ANN 模型,用于對網格的質量進行分類。這兩個 ML 模型都采用 7 個特征來表示網格的圖形。這些模型在實際乘用車的部件上進行了測試。在網格細化過程中,最初在相對粗糙的均勻網格上計算解。然后,估計后驗誤差。根據容錯值,在本地細化網格,直到獲得滿意的結果。
ML與單元特征
單元特征是指 FE 的屬性,它決定了單元模擬特定行為的能力。例如,一維桁架單元只能模擬軸向變形,而無法模擬剪切或彎曲變形。同樣,二維 (2D) 線性單元也無法模擬彎曲變形問題。這些功能由單元公式決定。單元計算中的兩個關鍵組成部分是形狀函數和數值積分點。接下來討論 ML 在形狀函數和數值積分點評估中的應用。
在有限元仿真中,一階拉格朗日最常用于近似幾何和主場變量。使用一階拉格朗日多項式的缺點是它在單元邊界上是C0連續的。此外,在分析之前必須選擇多項式的次數。通用近似特性使 ANN 成為用于計算形狀函數的良好候選者。對于給定的輸入節點坐標集,ANN 模型可以學習插值函數。
材質建模
本構模型描述了材料對外部載荷的響應。因此,數值結果的準確性在很大程度上取決于描述材料行為的適當材料模型的可用性。在傳統方法中,材料建模是指基于數學模型和經驗關系以及某些簡化假設的本構定律的發展。由于涉及復雜的物理場,使用傳統方法進行材料建模是具有挑戰性的領域之一,這使得該過程非常復雜且成本高昂。
Kirchdoerfer 和 Ortiz提出了一種新的計算方法,稱為數據驅動計算,其中實驗結果直接用于計算,而不考慮任何材料模型。該方法在滿足約束方程和守恒定律的同時,計算非線性 3D 桁架問題和非線性彈性實體的應力-應變關系。這項工作進一步擴展為開發一種更高效的數據驅動模型,稱為 max-ent 數據驅動計算,可以處理噪聲較大的材料數據。通過數據驅動方法進行的材料建模旨在通過最小化最小二乘意義上的距離函數,從預先指定的材料數據集中找到最接近的材料可能狀態。因此,這種方法的準確性在很大程度上取決于可用數據的質量和完整性。為了獲得必要的質量和數量數據,需要進行足夠數量的實驗。
通常,應力-應變數據用于使用 DL 對本構關系進行建模。這與發展本構關系有直接聯系。對于復雜模型來說,通過數值仿真或實驗獲得這些數據(應力-應變對)變得具有挑戰性。使用 DL 開發本構建模的另一種方法是使用間接數據(例如力和位移場),這些數據在測量值和基本本構關系之間沒有直接聯系,也更容易測量。中使用的 FE 代碼依賴于 TensorFlow 或 PyTorch 等自動微分包。此代碼生成的結果在用于傳統 FE 程序的裝配和求解器階段之前,需要進行額外的后處理。因此,這個補充處理步驟會為整個解決方案過程增加額外的時間。為了克服這一挑戰,DNN 與 Abaqus 集成,允許 DNN 和 Abaqus 之間進行數據通信。此外,將應力-應變數據視為歷史變量,在非彈性變形的彈性階段會出現額外的誤差。除了使用應力-應變作為歷史變量,累積的絕對總應變也可用于超彈性和塑性模型。
求解器
此步驟也稱為 FEA 的處理或求解器步驟。它涉及單元剛度矩陣、力矢量等元素量的計算,然后將這些量組裝成全局方程組。主要變量是通過在施加近似邊界條件后求解全局方程組來計算的。下面討論了 ML 在 FEA 求解器步驟中的應用。
為了計算單元剛度矩陣,Jung 等提出了一種深度學習模型,稱為深度學習有限元。該模型采用節點坐標以及八節點和四節點四邊形平面應力單元的泊松比作為輸入。該模型給出應變-位移矩陣作為輸出,用于計算單元剛度矩陣。
接觸
即使對于最簡單的問題,接觸影響分析也需要大量的計算工作。接觸影響分析的重要步驟之一是確定可能發生接觸的區域。它由兩個階段組成:一個全局搜索階段,用于查找可能的節點-段對,另一個本地搜索階段,用于查找段內接觸點的確切局部坐標。在找到正確的接觸位置后,通常通過求解最小距離搜索算法,使用各種技術(如罰、拉格朗日乘子、增廣拉格朗日乘子等)來應用接觸約束。
在分析開始之前,接觸區域是未知的。聯系人搜索階段需要花費大量精力才能正確識別聯系人位置。為了克服這個問題,Oishi 和 Yoshimura 提出了一種使用 ANN 的無迭代本地聯系人搜索方法。神經網絡預測接觸點的局部坐標值,同時將節點坐標作為輸入值。他們后來提出了一種快速穩定的無迭代曲面對曲面接觸搜索方法,該方法由 NURBS 使用 ML 定義。他們同時使用 ANN 和 SVM 來確定一對表面段是否接觸。
求解器
人工神經網絡的通用近似特性使它們能夠以所需的精度水平逼近任何函數,前提是網絡中有足夠數量的神經元。這一獨特的特性將 DL 推向了科學 ML 的新前沿。DL 已在多個領域得到應用,包括求解 PDE 和常微分方程 (ODE)。研究人員利用 DL 的強大功能,同時使用 DNN 和 CNN、PINN,來解決各種領域的 PDE 和 ODE。
由于無法獲得足夠的數據,絕大多數最先進的 ML 技術都缺乏穩健性,并且在分析復雜的物理、生物和工程系統時無法提供任何收斂保證。因此,在部分信息下得出結論。在一項開創性的貢獻中,Raissi 和合作者引入了物理信息神經網絡 (PINN) 的概念,在函數近似領域開創了一種新的范式。PINN 的本質在于其獨特的能力,不僅可以用作通用函數逼近器,還可以封裝控制給定數據集的本征物理學。這種范式超越了傳統的函數擬合范圍,結合了一般偏微分方程中編碼的基本物理原理的知識。此外,PINN 還具有處理正向和逆向問題的優勢。PINN 的基本方法是使用 DL 來最小化配置點的損失。這些配置點被認為是邊界點、初始點以及域中一些點的組合。損失函數由控制偏微分方程的殘差組成,包括作為懲罰參數的邊界項。
PINN 采用偏微分方程的強形式,并最大限度地減少 DNN 的殘差形式。雖然 FEM 和 PINN 的目標相同,但獲得解決方案的方法不同。在 PINN 中,邊界條件被合并到整個域的損失函數本身中,而 FEM 以單元形式施加邊界條件。研究人員提出了許多基于有限元法和PINN的研究方法,用于不同材料的力學分析:彈性、粘彈性、超彈性、塑性、超彈性。
模擬過程
耐撞性是指結構或系統在碰撞期間通過有效吸收和消散沖擊能量來保護乘員或有效載荷的能力。它涉及設計和工程措施,以盡量減少傷害和損害,最終提高乘員的安全性。由于其高度非線性的行為,處理碰撞現象是最具挑戰性的任務之一。在所需誤差范圍內捕獲崩潰事件需要非常多的仿真。考慮到車輛的成本、安全性和性能,車輛碰撞仿真對于確定最佳設計參數具有重要意義。ABAQUS、LS-DYNA、PAMCRASH、ANSYS等商業軟件包用于車輛碰撞仿真。這些模擬需要大量的計算資源和時間,因為有限元網格可能包含多達1000萬個單元。由于其巨大的計算成本以及機器學習與計算機進步的同步增長,耐撞性領域吸引了研究人員應用各種 ML 技術,以減少計算時間并簡化和加速耐撞性的設計過程。
為了以更少的計算時間分析碰撞仿真的結構響應,基于 FE 仿真數據構建了 ML 模型。Omar等使用RNN來確定車輛在撞擊過程中的碰撞特性。該模型采用 5 個輸入,其中包含當前狀態的位移、速度和加速度,以及前兩步的延遲加速度。RNN 模型預測新狀態的加速度,這決定了動態沖擊力。使用 ML 進行車輛碰撞分析涉及利用從 FE 仿真中獲得的高維數據。
損傷
損傷是由于外部載荷在材料內部形成微孔和微裂紋的過程,導致其性能惡化。損傷特征的分析可以通過基于模型或數據驅動的方法來進行。在基于模型的方法中,使用損傷變量評估材料的損傷狀態,這些變量可以是標量或張量。然后使用各種損傷增長定律研究損傷隨時間的演變,例如 Lemaitre、Tai 和 Yang、Chandrakanth 和 Pandey 或 Bonora 模型。制定本構方程來描述受損材料的機械行為,并使用 FEA 來解決由此產生的初始值問題。另一方面,數據驅動的方法,如SHM,使用傳感器來檢測和分析工程結構中的損傷。然而,基于 FEA 的損傷建模面臨著與復雜幾何形狀、內部結構、幾何非線性以及需要進行機械測試以確定材料特性相關的挑戰。SHM 還遇到了有關可靠性、專業知識要求、技術選擇、時間和成本的問題。為了應對這些挑戰,研究人員探索了使用各種 ML 算法來研究損傷和斷裂,提供了優于傳統 FEA 和 SHM 方法的潛在解決方案和改進。
SHM 涉及檢測損壞、定位損壞、量化其嚴重程度以及預測結構的剩余壽命。無損評估 (NDE) 等傳統方法成本高昂、耗時且需要專業知識。在 FEM 中,損傷分析涉及迭代求解前向問題。逆向分析根據動態響應預測損壞,但設置參數和專業知識帶來了挑戰。ML 通過利用數據來學習模式來克服這些挑戰,為 SHM 任務提供靈活且適應性強的框架。
斷裂
斷裂是一種特殊類型的損傷,當材料在過大的應力或負載下失效時,導致材料分離或斷裂成兩塊或多塊。斷裂可以突然發生,并且是災難性的(脆性斷裂),也可能逐漸發生,并伴有明顯的裂紋擴展(韌性斷裂)。斷裂通常以材料內部存在裂紋或裂縫為特征,是結構工程和材料科學中的關鍵問題。科學家們對預測聚合物復合材料斷裂韌性的不同 ML 算法進行了全面研究。
疲勞
疲勞是指材料在長時間內受到循環載荷或應力時發生的漸進性和局部損傷。當材料經歷重復的加載和卸載循環時,例如在機械部件或結構中,這一點尤其重要。Silva等使用粘接接頭的極端隨機樹(ERT)模型預測疲勞壽命。基于樹的模型是在相對較小的數據集上開發的,只有 365 個數據點。該模型將應力比、應力幅值、應力集中因子和三軸度(靜水應力與等效應力的比值)作為輸入。將基于樹的模型的性能與線性回歸模型的性能進行了比較。結果發現,基于樹的模型在預測疲勞壽命方面表現更好。Thakre 和 Kanjarla還使用隨機森林回歸來預測雙相鋼中的損傷起始應力。
為了研究疲勞行為,需要大量的載荷循環才能在兩個受振動的接觸表面之間產生裂紋。如果特定裂紋擴展行為所需的加載周期是先驗已知的,則可以顯著縮短此測試時間。為了減少測試時間,Gorji等使用ANN研究了C-Mn鋼在循環載荷下的裂紋擴展。ANN 模型以接觸寬度、峰值表面壓力和最大表面剪切為輸入,并預測裂紋深度的長度和閾值應力強度因子。
屈曲
屈曲是一種結構不穩定現象,當細長桿件受到壓縮載荷時突然發生橫向偏轉或彎曲,脫離其筆直和穩定的配置。這是一種關鍵的失效模式,可能導致結構和機械系統倒塌。
胡使用 ANN 預測碳纖維增強聚合物 (CFRP) 增強鋼柱的屈曲能力。這項工作還包括對 DNN 模型輸出相對于其 9 個輸入的敏感性分析。發現屈曲響應對所有 9 個輸入中柱子的長度和偏心率更敏感。然而,在實際應用中,在特定范圍之外出現任何長度和偏心率異常值的可能性非常小。網絡輸出相對于其他變量的敏感性較低,這意味著 ANN 模型的穩健性。這意味著,對于用于構建模型的數據范圍之外的參數,DNN 模型的預測準確性不會有太大偏差。
后處理
獲得有限元結果后,通過對主要變量(即位移、速度、溫度)進行導數來計算次要變量(即應變、應力、熱通量)。因此,與主變量相比,這些派生量的準確率較低。可以通過網格細化來提高精度。但是,這需要更高的計算成本。SPR是試圖提高這些推導量(應力)的準確性的技術之一。SPR 技術使用在高斯點處計算的應力值的多項式近似 。這種技術的缺點是它假定多項式的次數來描述應力場。這個假定的多項式場可能無法完全捕獲應力場。Khoei等使用ANN作為函數近似來計算應力場。使用 ANN 作為函數近似可以更準確地預測應力分布,尤其是在高應力梯度區域。在他們的方法中,為每個應力分量訓練了三種不同的 ANN 模型。
總結
在 FEA 環境中應用 ML 技術在 FEA 工作流程的各個階段(預處理、處理和后處理)都顯示出可喜的結果。將 ML 集成到 FEA 的各個階段具有巨大的優勢。它提高了計算效率,從而加快了分析和設計迭代的速度。基于 ML 的代理模型提供計算成本更低的近似解,從而能夠探索更大的設計空間。此外,ML 有助于逆向參數識別,有助于模型校準和優化。這些進步共同提高了 FEA 仿真的可靠性、速度和有效性,使工程師和研究人員能夠做出明智的決策,并在廣泛的行業和領域中實現更好的工程設計和分析結果。
-
仿真
+關注
關注
50文章
4099瀏覽量
133718 -
AI
+關注
關注
87文章
31097瀏覽量
269434 -
ML
+關注
關注
0文章
149瀏覽量
34669
原文標題:突破極限 :AI輔助有限元仿真
文章出處:【微信號:SinoEngineer,微信公眾號:中潤漢泰】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于MATLAB/Simulink的系統仿真技術與應用
淺析計算機仿真技術
Cadence PCB設計仿真技術
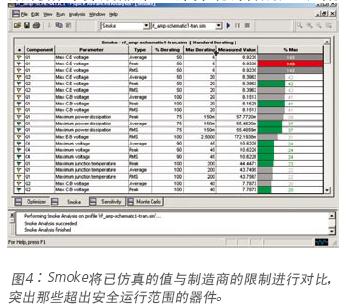




 AI輔助仿真技術方興未艾
AI輔助仿真技術方興未艾












評論