作者:京東物流 蘇裕焜
一、引言
在配送需求不斷增長的背景下,個人配送服務的大規模眾包化將對配送市場產生重大影響,且眾包定價涉及要素較多;這些變化意味著我們的營業部需要進行更精細化的定價管理,以適應眾包人員市場。與自營人員不同,眾包騎手的服務質量受到當地當時的人員可用性和成本波動的影響。為了提高騎手服務的攬派效率,降低整體運營經營成本,如何動態定價成為一個可考慮的選擇。通過動態定價,可以一定程度的幫助配送站點通過響應配送需求的變化來最大化收入并減少人員短缺;
在日常配送中,動態定價的優勢顯而易見。然而,在高峰時段或偏遠地區,臨時性的眾包騎手服務比全職騎手更復雜,需要更精細的規劃。價格的不確定性可能增加規劃和配送的難度。然而,如果眾包騎手可以提前儲備,那么報價也可以提前規劃并完成鎖定。這樣,配送站點可以規劃整個運營周期,并明確騎手服務的成本。這也是從過往一些營銷補貼案例中,對于券種選擇,觸達人員分析的一些思考,只是眾包的定價更強調周期性以及地區性,因此僅作為探索;
二、 MDP模型用于動態定價
站點眾包騎手的定價主要是基于路區難度系數,歷史單均等因素對未來的預測單量進行順序定價決策。因此,馬爾可夫決策過程(MDP)是可以作為一個基礎模型。MDP是其他動態定價工作的常用模型,尤其是當與強化學習結合時,如一些經典的充電樁分配問題。在這些案例中,狀態空間盡可能多地構建狀態變量,并從數據中學習定價策略。然而,由于訓練模型需要大量的計算資源來訓練歷史每天的運單數據與計費數據,強化學習的優先級會較低。在此選擇一些規則疊加聚類模型能更好的幫助我們進行歷史數據特征選擇和模型訓練。最后,可以參考其余案例使用泊松過程來模擬每個周期內單量需求的情況。通過將泊松過程應用于我們的離散時間模型在線動態定價中,并且可以定義為一種離散化誤差;
如圖所示,可以拆解為這幾步:
資源矩陣:在眾包騎手定價中,資源矩陣可以表示為不同時間段內可用的騎手資源。
產品定義:產品可以定義為特定時間段內的騎手服務組合。例如,產品 [1, 1, 0] 可以表示在三個時間段中的第一個和第二個時間段內提供騎手服務。
請求到達和預算:站點在不同時間提出對騎手服務的請求/需求,并提供他們愿意支付的報價預算(b1 到 b7)。
定價行動:營業部根據當前的騎手可用性和市場需求,采取動態定價策略(a1 到 a7)。每個定價決定都是基于當前資源狀態和預期需求。
接受與獎勵:當客戶接受報價(即,當他們的預算 bi 大于或等于定價 ai 時,用綠色的 ? 表示),營業部獲得一個獎勵 ri。這可以是收入或其他績效指標。同時,騎手資源的可用性根據所售產品的需求而減少。
資源管理:營業部需要持續監控和調整騎手的分配,以確保在滿足需求的同時最大化收入。這包括在高需求時段提高價格,或在低需求時段進行調價處理。
1. 眾包動態定價問題描述
眾包騎手服務的動態定價涉及為不同的配送產品(計費類型)在線設置最優或接近最優的價格,因為站點下不同路區、不同地址導致的報價都不盡相同。我們的配送站點將其資源——一組配送站的配送能力——組合成提供給客戶的產品,例如小時達等。 同樣的,對于不同的配送產品,公司內部的計費形式和計費價格都不盡相同,需要我們更精準更合理的進行資源分配;
由于對不同的配送產品的需求事先是未知的,但我們擁有關于攬派送的歷史數據、未來單量的一個粗粒度的預測數據以及不同時間段下單均成本變化數據。我們的目標是以一種方式可以定價每個到達該站點的攬派產品請求,以最大化目標函數,同時考慮需求的不確定性(季節性,大促活動等)。
那么在定價策略中,騎手和站點分別對應供應方和需求方的不同角色:
騎手(供應方):騎手是提供服務的主體,因此他們代表供應方。他們的可用性、工作時間、以及他們愿意接受的報酬水平都是供應方的關鍵因素。騎手的數量和他們的工作時間限制了站點能夠提供的服務數量。
站點(需求方):站點需要管理和激勵騎手,以滿足客戶的需求,因此在某種程度上站點也可以被視為需求方。站點需要制定價格策略來吸引足夠的騎手,同時也要考慮客戶的需求和支付意愿。站點通過定價策略來平衡騎手的供應和客戶的需求。
問題的供應方由一組 ( n ) 個資源組成,這些資源可以組合成 ( m ) 個可供出售的配送產品。每個產品由一個向量
? 表示,其中的元素規定了產品中使用的各個資源的數量。這些產品的可用性受到資源初始容量 (?) 和不同資源銷售期長度 (?) 的限制,這些長度決定了每個資源及其所在產品在何時之后不再可售(表示騎手在特定時間段內可用的時間窗口。在此時間之后,騎手可能不再可用,類似于資源過期。)。
問題的需求方通過一個非齊次復合泊松計數過程 (
?) 來建模,該過程模擬了不同時刻對于不同產品請求的到達,以及不同產品的有限內部客戶估值的分布 (?)。即站點需要在騎手的可用性和成本之間找到平衡。
2. MDP模型
在描述了眾包動態定價問題后,我們將嘗試開發一個馬爾可夫決策過程(MDP)模型,以確定定價策略 (
?)。定價策略是一個映射,它將價格 (a) 分配給站點-時間對 (?),并結合騎手資源的當前可用和計劃中的未來容量 (c)。
在我們的MDP中,定義為一個五元組 ((S, T, R, A, s_0)),騎手從某個初始狀態
? 開始。每個狀態捕捉當前的時間步、正在請求的站點以及當前可用的騎手數量。騎手為請求的站點提供一個價格 (?) ,采取一個行動,導致轉移到一個新狀態 (?)。然而,轉移并不是確定性的,因為尚不清楚騎手是否會接受或拒絕價格以及下一個站點請求是什么。通過將隨機需求過程 (?) 和騎手內估值的分布 (?) 擬合到歷史數據,我們可以估計轉移概率 (?,該概率決定了在狀態 (s) 下采取行動 (a) 時達到狀態 (s') 的可能性。狀態之間的轉移還會為騎手帶來由函數 (R(s, a, s')) 決定的獎勵。
從資料中查詢到的關于電動汽車充電動態定價的馬爾可夫決策過程(MDP)狀態的示意圖。該圖展示了資源在其銷售期結束后的過期情況(容量和產品向量中的灰色部分)。藍色方塊表示MDP狀態。在時間步 (t),充電站的容量通過容量向量 (c_t) 表示。向量的元素代表相應時間段(綠色方塊中的時間范圍)內的可用充電容量。從上一個時間步開始到達的可能充電會話預約請求由向量 (p_t) 表示,其中1表示請求的時間段。基于三個狀態變量 (c_t)、(t)、(p_t),定價策略提供一個動作 (a),即充電價格,用戶可以接受(底部的前兩個狀態)或拒絕(右側的狀態)。然后狀態轉移到下一個時間步(轉移函數的詳細信息在圖4中說明)。接受的充電請求會導致容量值減少。下一個充電會話預約被輸入到新狀態中。注意,時間步的分辨率必須比充電時間段更精細。灰色顯示了關于充電容量和會話向量 (c_t) 和 (p_t) 的過去信息。
而如果我們的項目需要進行相關的框架復用,可以類比騎手資源在其服務期結束后的過期情況(在容量和任務向量中的灰色部分)。藍色方塊表示MDP狀態。
在時間步 (t),騎手的可用數量通過容量向量 (c_t) 表示。向量的元素代表相應時間段內可用的騎手數量。從上一個時間步開始到達的可能訂單請求由向量 (p_t) 表示,其中1表示請求的時間段。
基于三個狀態變量 (c_t)、(t)、(p_t),定價策略提供一個動作 (a),即服務價格,用戶可以選擇接受(底部的前兩個狀態)或拒絕(右側的狀態)。然后狀態轉移到下一個時間步(轉移函數的詳細信息可以通過類似的圖進行說明)。接受的訂單請求會導致可用騎手數量減少。下一個訂單請求被輸入到新狀態中。
在調整后的框架下:
容量向量 (c_t):表示在不同時間段內的可用騎手數量。
訂單請求向量 (p_t):表示在不同時間段內的訂單請求情況。
定價策略 (a):根據當前狀態決定的服務價格。
狀態轉移:訂單被接受后,騎手的可用數量會減少,未被接受的訂單則不影響騎手數量。
2.1 狀態空間
眾包項目中,MDP的狀態空間 (S) 由狀態 (s = (c, t, p)) 組成。這里,(c) 表示當前時刻可用的騎手資源數量,(t) 是離散化的時間步,(p) 是客戶在該時間步請求的產品類型。通過將整個服務時間段(0, max(T))離散化為 (k) 個時間步,我們確保狀態空間是有限的。雖然可以使用連續時間MDP,但這會增加問題的復雜性,并使解決方案更難以實現。客戶請求到達時間是連續的,但在我們的模型中被視為離散事件。我們假設在相似時間到達的客戶請求表現出相似的行為,即需求隨時間以分段連續的方式變化,具有有限的不連續性。
2.2 動作空間
MDP的動作空間 (A) 是騎手可以提供給客戶的可能價格集合。雖然理論上價格集合可以是連續的,但在實踐中,我們假設價格是一個有限集合。這種離散化反映了大多數服務提供商在定價時的做法。特別地,有一個特殊的價格 (a = infty),表示拒絕動作,因為沒有客戶會接受無限高的價格。當騎手資源不足以滿足請求時,采用此動作。
2.3 獎勵函數
MDP的獎勵函數 (
?) 確定了通過采取動作 (a) 從 (s_t) 轉移到 (s_{t+1}) 所獲得的獎勵。若目標是最大化收入,則獎勵為提供給客戶的價格。當客戶接受報價時,獎勵為動作 (a) 的值,否則為0。成功的交易意味著騎手資源從 (c) 減少到 (c - p)。
2.4 轉移函數
轉移函數 (
?) 是MDP模型中最復雜的部分,它決定了采取動作 (a) 后系統如何從狀態 (s_t) 轉移到 (s_{t+1})。此函數由客戶請求的到達過程 (D(t)) 和客戶對產品的內部估值分布 (?) 決定。在狀態 (s_t = (c, p)) 中,騎手為客戶請求的產品 (p) 選擇一個價格 (a)。客戶接受報價的概率由估值分布 (?) 的補充累積分布函數? 決定。
客戶請求的到達過程 (D(t)) 基于復合泊松計數過程 (
?),假設客戶到達時間具有無記憶性。我們將泊松過程離散化為多類伯努利過程 (D(t)),在每個時間步最多允許一個產品請求。通過選擇適當的時間步數 (k),確保離散化過程 (D(t)) 能夠很好地近似泊松過程 (?)。
三. MDP模型的離散需求過程
我們嘗試使用了一個離散需求過程來模擬每個客戶請求的泊松到達過程。
離散需求過程的定義:
假設整個服務時間段 ((0, T)) 被縮放為單位時間段 ((0, 1)),這可以通過簡單的時間線重新縮放實現。
對于每種客戶請求的產品 (p in P),我們假設有一個泊松計數過程 (N_p(tau)),其到達率為 (lambda_p),用于生成該產品的請求到達時間。
所有產品請求的到達時間可以被視為一個復合泊松過程 (N(tau)),其強度為 (lambda = sum_{p in P} lambda_p)。
離散化的必要性:
因為時間被離散化為 (k) 個時間步,我們需要用離散的伯努利過程來逼近泊松過程的到達。
伯努利過程是一系列伯努利試驗,定義為 (k) 次試驗和每次試驗中任何請求到達的概率 (p)。
這種逼近基于泊松過程是通過保持 (kp = lambda) 不變并讓 (k to +infty) 的伯努利過程序列的極限。
單個產品請求的分配:
我們可以通過根據概率分配產品索引來重建單個產品的到達過程。 在伯努利過程中,可以通過采樣離散分布來將到達分配給產品類型。
逼近質量取決于將連續服務時間段 ((0, 1)) 劃分為 (k) 個時間步的值 (k)。
離散需求過程的期望請求數量與泊松過程的期望到達數量在((0, 1))區間內相匹配,因此在這個指標上兩者沒有差異。
以下是模擬的偽代碼,供參考
# 輸入參數 stations = [s1, s2, ..., sn] # 站點集合 riders = [r1, r2, ..., rm] # 騎手集合 products = [p1, p2, ..., pk] # 產品集合 zones = [z1, z2, ..., zl] # 路區集合 lambda_p = [λ1, λ2, ..., λk] # 各產品的到達率 historical_prices = {...} # 歷史報價數據 historical_volumes = {...} # 歷史單量數據 predicted_volumes = {...} # 預測單量數據 pricing_types = ["fixed", "dynamic", "promotional"] # 計費類型 # 時間步設置 T = 1 # 單位時間段 k = 100 # 時間步數 # 初始化請求到達矩陣 requests = [[[[0 for _ in range(k)] for _ in range(len(zones))] for _ in range(len(products))] for _ in range(len(stations))] # 模擬請求到達過程 for t in range(k): for station in stations: for product_index, product in enumerate(products): # 預測到達率調整 adjusted_lambda = adjust_lambda(lambda_p[product_index], historical_volumes, predicted_volumes, station, product) # 計算每個時間步的到達概率 p = adjusted_lambda / k # 在當前時間步內是否有請求到達 if random_bernoulli(p): # 確定請求的路區 zone_index = sample_zone_distribution(zones, historical_volumes, station, product) # 增加對應產品和路區的請求計數 requests[stations.index(station)][product_index][zone_index][t] += 1 # 動態定價策略 def dynamic_pricing(station, product, zone, time_step): # 使用歷史報價和單量調整價格 base_price = historical_prices[(station, product, zone)] demand_factor = calculate_demand_factor(historical_volumes, predicted_volumes, station, product, zone, time_step) # 定價策略:基于歷史數據和當前需求 if pricing_types[product] == "dynamic": price = base_price * (1 + demand_factor) elif pricing_types[product] == "promotional": price = base_price * (1 - 0.1) # 例如促銷打九折 else: # fixed price = base_price return price # 輔助函數:伯努利試驗 def random_bernoulli(probability): return random.uniform(0, 1) < probability # 輔助函數:從路區分布中采樣 def sample_zone_distribution(zones, historical_volumes, station, product): # 根據歷史單量在不同路區的分布進行采樣 zone_distribution = calculate_zone_distribution(historical_volumes, station, product) random_value = random.uniform(0, 1) cumulative_sum = 0 for index, probability in enumerate(zone_distribution): cumulative_sum += probability if random_value < cumulative_sum: return index return len(zones) - 1 # 返回最后一個索引作為默認 # 輔助函數:調整到達率 def adjust_lambda(base_lambda, historical_volumes, predicted_volumes, station, product): # 根據歷史和預測數據調整到達率 adjustment_factor = predicted_volumes[(station, product)] / historical_volumes[(station, product)] return base_lambda * adjustment_factor # 輸出請求到達矩陣和價格策略 print(requests) for station in stations: for product in products: for zone in zones: for t in range(k): price = dynamic_pricing(station, product, zone, t) print(f"Price for {station}, {product}, {zone} at time {t}: {price}")
四. 使用蒙特卡羅樹搜索(MCTS)
蒙特卡羅樹搜索(Monte Carlo Tree Search, MCTS)是一種用于決策過程的啟發式搜索算法,廣泛應用于博弈論和其他復雜決策問題。MCTS通過隨機模擬來探索可能的決策路徑,逐步構建決策樹,以找到最優策略。以下是MCTS的基本組成部分和工作原理:
選擇(Selection):
從根節點開始,使用選擇策略(如UCB1,Upper Confidence Bound for Trees)在樹中選擇一個子節點,直到到達一個未完全擴展的節點。
UCB1策略通過平衡探索(探索不太確定的節點)和利用(利用當前已知最優的節點)來選擇節點。
擴展(Expansion):
如果選擇的節點不是終止狀態且可以擴展,則添加一個或多個子節點。每個子節點表示一個可能的動作或狀態。
從擴展的節點開始,進行隨機模擬直到達到終止狀態。這個過程通常稱為“rollout”。
在仿真過程中,隨機選擇動作來模擬未來的可能路徑,以估計該路徑的潛在獎勵。
回溯(Backpropagation):
將仿真得到的獎勵回溯更新到經過的每個節點。更新節點的統計信息,如訪問次數和平均獎勵。
這種更新有助于逐漸提高對不同路徑的估計準確性。
在一些復雜系統中,MDP可以用于建模和提供初步策略,而MCTS可以在實時操作中進行具體的決策優化和調整。這種結合可以充分利用兩者的優勢,適應不同的需求和約束。
下面是探索過程中的脫敏偽代碼:
function MCTS(root_state, iterations):
root_node = CreateNode(state=root_state)
for i from 1 to iterations do:
# Selection
node = root_node
while node is fully expanded and not terminal(node) do:
node = BestChild(node, exploration_param)
# Expansion
if not terminal(node) then:
node = Expand(node)
# Simulation
reward = Simulate(node.state)
# Backpropagation
Backpropagate(node, reward)
return BestAction(root_node)
function CreateNode(state):
return Node(state=state, parent=None, children=[], visits=0, total_reward=0)
function BestChild(node, exploration_param):
best_score = -Infinity
best_child = None
for child in node.children do:
exploit = child.total_reward / child.visits
explore = exploration_param * sqrt(log(node.visits) / child.visits)
score = exploit + explore
if score > best_score then:
best_score = score
best_child = child
return best_child
function Expand(node):
action = UntriedAction(node)
next_state, reward = SimulateAction(node.state, action)
child_node = CreateNode(state=next_state)
child_node.parent = node
node.children.append(child_node)
return child_node
function Simulate(state):
current_state = state
total_reward = 0
while not terminal(current_state) do:
action = RandomAction(current_state)
next_state, reward = SimulateAction(current_state, action)
total_reward += reward
current_state = next_state
return total_reward
function Backpropagate(node, reward):
while node is not None do:
node.visits += 1
node.total_reward += reward
node = node.parent
function BestAction(root_node):
best_action = None
best_value = -Infinity
for child in root_node.children do:
value = child.total_reward / child.visits
if value > best_value then:
best_value = value
best_action = child.action
return best_action
function SimulateAction(state, action):
# Simulate the effect of an action in the environment
next_state = TransitionFunction(state, action)
reward = RewardFunction(state, action, next_state)
return next_state, reward
function UntriedAction(node):
# Return an action that has not been tried yet from this node
# This function should consider the set of possible actions and filter out those already tried
return SomeUntriedAction(node.state)
function RandomAction(state):
# Return a random action from the set of possible actions for the given state
return SomeRandomAction(state)
function terminal(state):
# Determine if the state is a terminal state
return IsTerminalState(state)
五. 結論說明
我們嘗試描述了一種基于馬爾可夫決策過程(MDP)的動態定價模型,用于優化眾包騎手的服務分配和定價策略。隨著眾包配送服務的快速增長,這種模型可能成為未來物流和配送系統的重要組成部分。該模型允許眾包平臺在為客戶提供靈活且高效的配送服務的同時,最大化其收入。
為了解決我們的MDP模型,還嘗試使用蒙特卡羅樹搜索(MCTS)啟發式算法來優化定價決策。在實際項目中還需要明確定價算法是否優于固定費率基線,并且在可以獲得該基線的情況下,與最優價值迭代(VI)基線是否具有競爭力。
在一些別的定價項目中,會看到有同學采取因果推斷的方式進行定價選擇、價格補貼,這可能取決于我們的具體目標和問題特性。如果目標是動態地優化定價策略或資源分配策略,以便在不斷變化的環境中最大化收益(如利潤、效率或客戶滿意度),MDP是也是一個合適的選擇。MDP可以幫助我們在不同狀態下制定最優行動策略,并有效處理不確定性,通過概率模型預測不同狀態的轉移和相應的獎勵。另一方面,如果我們希望理解某些因素(如定價策略、激勵措施)對騎手行為或客戶需求的因果影響,因果推斷也可以作為補充加入。因果推斷可以幫助識別哪些因素真正驅動了結果變化,并評估新策略的效果,尤其是在數據中存在混雜因素時,因果推斷方法可以提供更準確的因果估計。
在后續項目中,結合兩者的方法可能會更有效,例如,先使用因果推斷識別關鍵因果關系,然后在MDP中利用這些關系進行優化決策。
參考來源:
【1】J. Gao, T. Wong, C. Wang, and J. Y. Yu, “A Price-Based Iterative Double Auction for Charger Sharing Markets,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 6, pp. 5116–5127, Jun. 2022, issn: 1558-0016. doi: 10.1109/TITS.2020.3047984. [Online]. Available: https://ieeexplore.ieee.org/document/9325919 (visited on 08/09/2024)
【2】P. V. Dahiwale, Z. H. Rather, and I. Mitra, “A Comprehensive Review of Smart Charging Strategies for Electric Vehicles and Way Forward,” IEEE Transactions on Intelligent Transportation Systems, pp. 1–21, 2024, issn: 1558-0016. doi: 10.1109/TITS.2024.3365581. [Online]. Available: https://ieeexplore.ieee.org/document/10457989 (visited on 08/08/2024)
審核編輯 黃宇
-
mDP
+關注
關注
0文章
9瀏覽量
9556 -
模型
+關注
關注
1文章
3255瀏覽量
48905
發布評論請先 登錄
相關推薦
易飛揚走過2024——避開紅海 專注差異化
螞蟻集團收購邊塞科技,吳翼出任強化學習實驗室首席科學家
運營商如何實現差異化連接
如何使用 PyTorch 進行強化學習
「騰訊IoT Video+微信小程序」覓感貓眼方案助力鎖廠打造差異化產品優勢

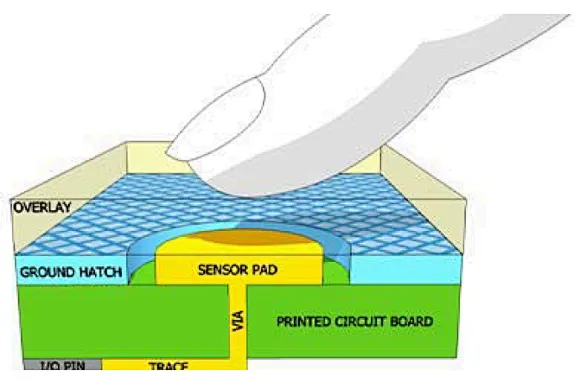
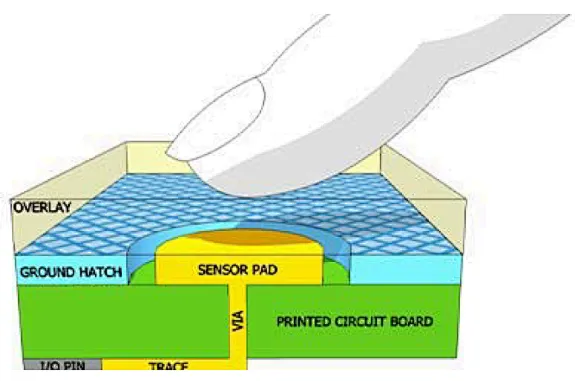
英飛凌 | 用電容式觸摸感應技術實現HMI差異化解決方案
江蘇移動攜手華為率先完成全省范圍智能差異化體驗保障商用驗證
鴻蒙ArkUI-X平臺差異化:【運行態差異化(@ohos.deviceInfo)】
探索IPE差異化體驗,助力浙江移動網絡價值變現
華為攜手中國移動浙江公司 實現全球首個5G-A核心網智能差異化體驗保障
用電容式觸摸感應技術實現HMI差異化解決方案




 強化學習在眾包差異化定價中的探索
強化學習在眾包差異化定價中的探索













評論