背景介紹

本文是基于我們之前的 RPN（Reconciled Polynomial Network）研究的后續工作。在此前的研究中，我們提出了 RPN 這一通用模型架構，其包含三個組件函數：數據擴展函數、參數調和函數和剩余函數。

我們先前的研究表明，RPN 在構建不同復雜性、容量和完整性水平的模型方面具有很強的通用性，同時可以作為統一多種基礎模型（包括 PGM、核 SVM、MLP 和 KAN）的框架。

然而，先前的 RPN 模型基于以下假設：訓練批次中的數據實例是獨立同分布的。此外，在每個數據實例內部，RPN 還假定所涉及的數據特征彼此獨立，并在擴展函數中分別處理這些數據特征。

不過，現實數據往往存在比較強的相互依賴關系，這種依賴關系既存在于樣本之間，也存在樣本內部各個數據特征之間。

如上圖中 (a)-(d) 所示， 對于圖像、語言、時間序列和圖等復雜且具有相互依賴的數據，這使得先前 RPN 模型的獨立假設不成立。如果像先前的 RPN 模型那樣忽略這些數據的相互依賴性，學習性能將顯著下降。

RPN 2 模型結構

為了解決上面提到的問題，在本文中，我們重新設計了 RPN 架構，提出了新的RPN 2（即Reconciled Polynomial Network 2.0）模型。如上圖中所示，RPN 2 引入了一個全新的組件——數據依賴函數，用于顯式建模數據實例和數據特征之間的多種依賴關系。

這里需要解釋一下，雖然我們在本文中將該組件稱為“依賴函數（interdependence function）”，但實際上，該函數捕獲了輸入數據中的多種關系，包括結構性依賴、邏輯因果關系、統計相關性以及數值相似性或差異性等。

在模型架構方面，如上圖所示，RPN 2由四個組成函數構成：數據擴展函數（data expansion function）、數據依賴函數（data interdependence function）、參數調和函數（parameter reconciliation function）、和余項函數（remainder function）。數據擴展函數：根據數據擴展函數的定義，RPN 2 將數據向量從輸入空間投射到中間隱層（更高維度）空間，投射后的數據將由新空間中的新的基向量表示。數據依賴函數：根據數據和底層模態結構信息，RPN 2 將數據投射到依賴函數空間，投射后的數據分布能夠有效地獲取數據樣本和特征之間的相互依賴關系。參數調和函數：為了應對數據擴展帶來的“維度災難”問題，RPN 2 中的參數調和函數將一組減少的參數合成為一個高階參數矩陣。這些擴展的數據向量通過與這些生成的調和參數的內積進行多項式集成，從而將這些擴展的數據向量投射回所需的低維輸出空間。余項函數：此外，余數函數為 RPN 2 提供了額外的補充信息，以進一步減少潛在的近似誤差。

RPN 2 深度和廣度的模型結構

RPN 2 提供了靈活的模型設計和結構，并且允許用戶搭建不同深度和廣度的模型結構。

上圖展示了 RPN 2 的多層（K層）架構，每一層包含多個頭部（multi-head）用于函數學習，這些頭部的輸出將被融合在一起。右側子圖展示了 RPN 2 頭部的詳細架構，包括數據變換函數、多通道參數調和函數、余項函數及其內部操作。

屬性和實例的相互依賴函數會計算相互依賴矩陣，該矩陣將應用于輸入數據批次，位置可以是在數據變換函數之前或之后。虛線框內黃色圓角矩形表示可選的數據處理函數（例如激活函數和歸一化函數），這些函數可作用于輸入、擴展以及輸出數據。

多模態數據底層結構和依賴函數

本文還專門分析了幾種常見數據的底層模態結構，包括圖像、點云、語言、時序、和各類圖結構數據。如下圖所示：

grid：圖像和點云表示為網格結構數據，其中節點表示像素和體素，連邊表示空間位置關系；

chain：語言和時間序列數據表示為鏈式結構數據，其中節點表示詞元和數值，連邊表示順序關系；

graph：分子化合物和在線社交網絡表示為圖結構數據，其中節點表示原子和用戶，連邊表示化學鍵和社交連接。

4.1 圖像和點云數據幾何依賴函數

對于圖像和點云，每個 pixel （或者 voxel）之間的依賴關系往往存在于圖像和點云數據的局部。換而言之，我們可以從輸入的圖像和點云數據中劃分出局部的 patch 結構，用來描述 pixel 和 voxel 之間的依賴范圍。

在傳統模型中，這種 patch 的形狀往往需要認為定義，其形狀可以是cuboid shape，cylinder shape，sphere shape。而從 grid 中定義 pixel （或者 voxel）依賴范圍的過程可以表示為 patch packing 這一經典幾何學問題。

取決于 patch 的形狀，本文提出了多中 packing 的策略用來定義依賴函數，以平衡獲取輸入數據信息的完整度和避免數據冗余。

4.2 語言和時序數據拓撲依賴函數

除了基于 grid 的幾何依賴函數之外，本文還介紹了基于 chain 和 graph 的拓撲依賴函數。鏈式結構依賴函數和多跳鏈式依賴函數主要用于建模數據中的順序依賴關系，這種關系廣泛存在于自然語言、基因序列、音頻記錄和股票價格等數據中。

基于序列數據，本文定義了多種基于 chain 結構的拓撲 single-hop 和 multi-hop 的依賴函數。其中 single-hop chain 結構的拓撲依賴函數分為單向和雙向兩種。如下圖所示，單向依賴強調元素僅依賴于前一個，而雙向依賴則考慮元素同時依賴于前后鄰居，從而捕捉更全面的上下文信息。

為了高效建模長鏈數據中的多跳依賴關系，multi-hop chain 結構的拓撲依賴函數引入了跳數（hop）參數，直接描述鏈中某一元素與多跳范圍內其他元素的信息交互。同時，通過累積多跳函數聚合多個跳數的信息，進一步擴展了特征捕獲范圍。

4.3 圖結構數據拓撲依賴函數

不僅如此，如下圖所示，本文還提出了基于 graph 結構的拓撲依賴函數。圖結構依賴函數和基于 PageRank 的圖結構依賴函數旨在建模復雜數據之間的廣泛依賴關系，特別是以圖為基礎的數據，如社交網絡、基因互動網絡等。

在圖結構依賴函數中，數據的依賴關系被表示為一個圖 G=(V,E)，其中節點表示屬性或數據實例，邊表示它們之間的依賴關系，對應的依賴矩陣 A 則是圖的鄰接矩陣。基于該圖結構，函數通過矩陣運算建模節點之間的多跳依賴關系，并引入累積多跳函數以整合多層次的信息交互。

進一步地，基于 PageRank 的圖依賴函數利用圖的隨機游走思想，通過收斂矩陣高效地建模全局的長距離依賴關系，并支持多種矩陣歸一化策略以增強計算的穩定性和靈活性。

RPN 2 依賴函數列表

除了上述提到的依賴函數之外，本文還提出了多中依賴函數用來建模多種類型數據之間的依賴關系。通過有效地使用這些依賴函數和其他函數，我們可以構建更加有效的模型架構，使 RPN 2 能夠應對廣泛的學習挑戰。

在本文中，我們總共提出了 9 大類，50 多種的數據依賴函數，部分依賴函數的表示和基本信息都總結在了上面的列表中。

深度學習模型的統一表示：CNN, RNN, GNN 和 Transformer

RPN 實現了豐富的功能函數，具體列表如上圖所示。通過組合使用上述功能函數，RPN 2 不僅可以構建功能強大的模型結構，并且可以統一現有基礎模型的表示，包括 CNN，RNN，GNN 和 Transformer 模型。

實驗驗證

為了驗證提出的 RPN 2 模型的有效性，本文通過大量的實驗結果和分析，證明了 RPN 2 在多種 Function Learning Task 上的有效性。

在本文中，具體的實驗任務包括：離散圖片和文本分類，時序數據預測，和圖結構數據學習等。7.1 離散圖片和文本分類在本文中，我們在離散圖片和文本數據集上測試了 RPN 2 的實驗效果，包括：

MNIST 圖片數據集

CIFAR10 圖片數據集

IMDB 文本數據集

SST2 文本數據集

AGNews 文本數據集

我們不僅跟先前的 RPN 1 模型進行了對比，也和傳統的 MLP 和 CNN/RNN 模型進行了對比，具體結果如下表所示：

Note: 本文實驗所使用的數據集，都沒有使用基于 flipping，rotation 等技術進行數據增強。上表展示了各個方法在多個數據集上分類的 Accuracy score。

7.2 圖片數據依賴擴展

對于圖片數據，RPN 2 使用了基于 cylinder patch shape 的依賴函數。下圖也展示了部分圖片基于 RPN 2 所學得的數據表示，其中圖片中的每個 pixel 都被擴展成了一個 cylinder patch shape，每個 cylinder patch 包含了每個 pixel 周圍的有效的 context 信息。

7.3 時序數據預測

RPN 2 也可以有效地擬合時序數據，本文使用了四個時序數據集來驗證 RPN 2 在時序數據擬合和預測的有效性，包括：

Stock market dataset

ETF market dataset

LA traffic record

Bay traffic record

如下表所示，通過使用 chain 結構的依賴函數，RPN 2 可以有效的獲取時序數據之間的依賴關系，并且在各個數據集上都獲得有效的學習結果。

Note: 上表中的結果是各個方法在幾個時序數據集上預測結果的 MSE。

圖結構數據學習

為了驗證 RPN 2 在圖結構數據上的有效性，本文也提供了各個方法在 graph 結構數據上的學習結果，包括：

Cora graph

Citeseer graph

Pubmed graph

如下表所示，基于 graph 依賴函數和復合依賴函數（包括 graph 和 bilinear 依賴函數），RPN 2 在多個 graph 數據集上都可以獲得比 GCN 都優的節點分類的結果。

Note: 上表中的結果是各個方法在幾個 graph 數據集上 node 分類結果的 Accuracy。

于RPN 2的模型泛化誤差分析

除了實驗驗證之外， 本文還提供了基于 RPN 2 的模型泛化誤差的理論分析，其分析結果對目前主流的深度模型（例如 CNN, RNN, GNN 和 Transformer）都適用。

本文的模型泛化誤差是基于給定的數據集 D 來進行分析，其中 D 的一部分可以作為訓練集用來進行模型訓練，我們可以定義模型產生的誤差項如下圖所示：

本文中，模型泛化誤差是指 ，即模型在未見到的數據樣本上所產生的誤差和在訓練數據樣本上產生的誤差的差別：

9.1 基于VC-Dimension泛化誤差分析基于 RPN 2 的模型結構，我們定義了模型的 VC-Dimension 如下圖所示：

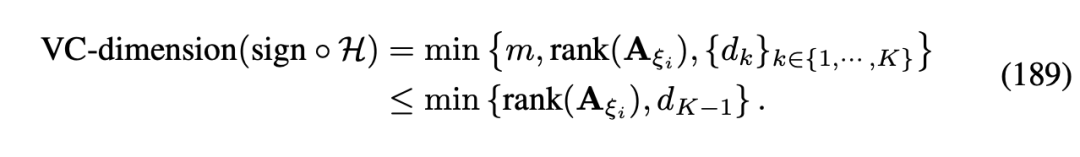
根據所獲得的 VC-Dimension 我們定義了 RPN 2 模型的泛化誤差如下圖所示：

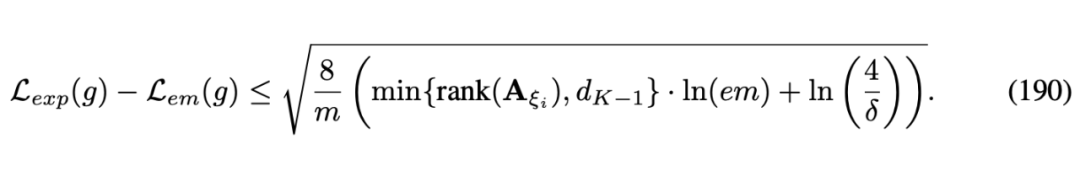
9.2 基于Rademacher Complexity泛化誤差分析

除了 VC-dimension 之外，我們還基于 Rademacher Complexity 理論分析了模型的泛化誤差。相比 VC-dimension，Rademacher Complexity 不僅僅考慮了 RPN 2 模型結構，還考慮了輸入數據對泛化誤差的影響。

基于提供的 RPN 2 模型，我們定義了模型 Rademacher Complexity 如下圖所示：

根據定義的 Rademacher Complexity，我們進一步分析了 RPN 2 泛化誤差如下圖所示：

上述模型泛化誤差分析不僅僅可以從理論上解釋現有模型表現的區別，也為將來模型的設計提供了一下啟示，特別是針對依賴函數的設計。

RPN 2討論：優點，局限性，以及后續工作10.1 RPN 2優點

本文通過引入建模屬性和實例間關系的數據依賴函數，對 RPN 2 模型架構進行了重新設計。基于實驗結果和理論分析，所提出的依賴函數顯著提升了 RPN 2 模型在處理復雜依賴數據時的學習能力，具體貢獻包括以下三方面：

理論貢獻：與假設數據獨立同分布的舊版模型不同，新設計的 RPN 2 模型通過一組基于輸入數據批次的依賴函數，能夠有效捕捉屬性與實例之間的依賴關系，從而大幅擴展模型的建模能力。

此外，本文提供的理論分析（基于 VC 維和 Rademacher 復雜度）展示了如何定義最優依賴函數以減少泛化誤差。這些依賴函數還從生物神經科學角度模擬了神經系統的某些補償功能，為功能學習任務提供新的啟發。