? 背景引入 ?
近年來,得益于光學、電子和計算機等各項技術的進步以及新算法的不斷提出,計算全息技術飛速發展。由于現有液晶空間光調制器對于純相位全息圖具有更高的調制能力與衍射效率,純相位全息圖優化算法一直以來都是研究熱點。目前,各種傳統方法可以滿足不同的計算耗時與重建質量要求,而深度學習、維爾丁格流等新方法為純相位全息圖優化帶來了新的思路,這些工作都有利于實時、廣視場、高質量全息三維顯示的早日實現。不同于傳統的全息成像技術,在計算機生成全息圖領域,液晶空間光調制器帶來了對波前信息前所未有的靈活控制能力,為計算全息的發展提供了很大的發展空間與動力。

過去的幾十年間,計算機生成純相位全息圖算法層出不窮,其核心就是純相位全息圖優化問題: 給定一個復振幅全息圖(Complex-Amplitude Hologram),將其編碼成為一個純相位全息圖(Phase-Only Hologram),使得用該純相位全息圖進行光學重建所得到的圖像要盡可能還原原始圖像。這些方法主要分為3類:迭代方法、非迭代方法與其他方法。迭代算法通常由一個對目標全息圖的近似出發,經過一系列的重復操作不斷優化這個近似全息圖,直到該近似所得到的重建圖像滿足一定的誤差要求;非迭代算法不需要重復的大量優化計算, 會根據指定步驟一次性給出近似解。由于較低的計算負荷,非迭代算法更符合實時全息顯示的要求,而代價是這類方法的重建質量不如迭代算法;其他方法種類繁多,各有特點。
? 純相位全息圖生成算法介紹 ?
迭代性算法:Gerchberg-Saxton算法
可以生成純相位全息圖的迭代算法中,迭代傅立葉變換算法 (IterativeFourier Transform Algorithm)是一種比較具有代表性的算法,該類算法的特點是通過傅立葉變換在兩個平面中的反復傳遞。
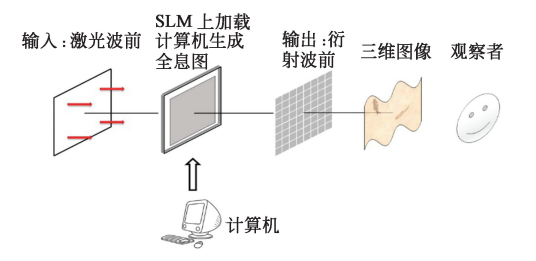
圖1 計算機生成全息成像術流程圖
迭代傅立葉變換算法,或稱誤差減少算法(Error Reduction Algorithm)在20世紀70年代早期被作為數字全息的一種算法而提出, 后來被 Gerchberg與 Saxton修改并運用在相位提取領域,成為了迭代算法中最著名也可能是被運用最多的方法—Gerchberg-Saxton(GS)算法,其算法流程圖如圖2。
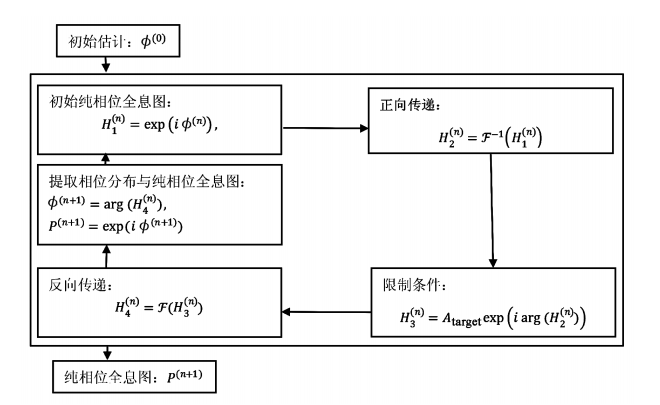
圖2 Gerchberg-Saxton算法流程圖
該算法中,根據全息圖平面與重建圖像平面的振幅分布,通過迭代進行正逆向的光波傳遞以及施加在兩個平面上的限制條件, 進而求得全息圖平面中光場的相位信息。該方法在計算純相位全息圖場景中十分適用,可以使用菲涅爾變換或者傅立葉變換來進行光場傳播的計算。
迭代性算法:誤差擴散算法
誤差擴散算法(Error Diffusion Method)是另一種類型的迭代算法,該算法會在全息圖平面的各個像素之間迭代。當復振幅全息圖的振幅信息被直接移除時,每個像素點都會產生誤差,而誤差擴散算法將逐個掃描像素點,并將每個像素點的誤差按照一定權重向尚未掃描到的四個相鄰像素點擴散。
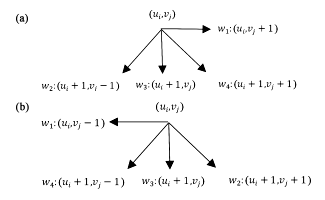
圖3 誤差擴散算法示意圖;(a)誤差從左向右掃描擴散;(b)誤差與從右向左掃描的擴散。
? 非迭代性算法 ?
隨機相位方法在全息圖純相位化的過程中是一種常用的非迭代方法。由于純相位全息編碼相當于高頻濾波過程,重建圖像只包括原始圖像的邊界與線條部分,因此需要引入隨機相位掩膜(Random Phase Mask)使原始圖像的波前分散至整幅全息圖以提高重建質量,然而隨之而來的斑點噪聲也較明顯。為了減少這種斑點噪聲,近期有一種改進的隨機相位方法,該方法會針對不同的圖像,引入具有不同頻率的隨機相位掩膜以進一步減少信息損失和提高重建質量。除此之外,還有許多用于減少斑點噪聲的非迭代方法,例如:采用下采樣掩膜的采樣純相位全息圖(Sampled-Phase-only Hologram)方法、模式化相位掩膜(Patterned Phase-Only Hologram)方法、雙相位方法(Double-Phase Method),以及使用非隨機相位掩膜的方法(Random Phase-Free Method)等。
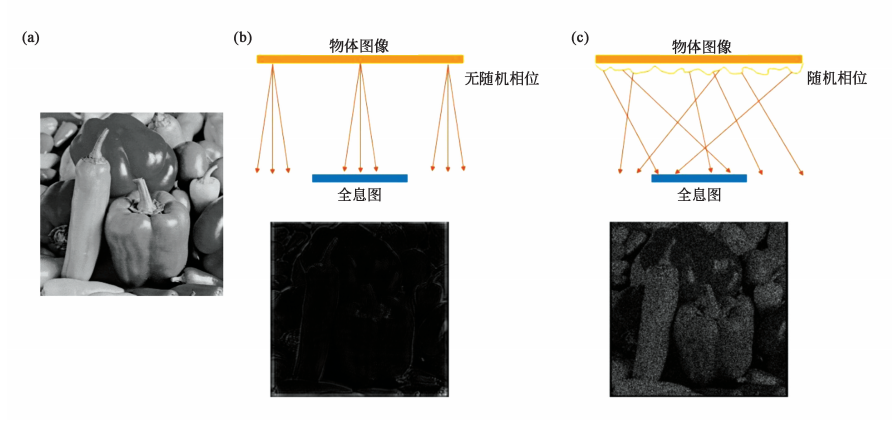
圖4 隨機相位對純相位全息圖重建結果作用示例;(a)原始圖像;(b)未添加隨機相位掩膜;(c)添加隨機相位掩膜。
? 其他方法 ?
除了迭代算法與非迭代算法,有一種直接算法可以用于計算純相位全息圖。假設純相位全息圖有M×N個像素,每個像素點的相位值有Q種可能取值,則純相位全息圖生成問題的搜索空間為M×N×Q,目標是找到重建圖像與原始圖像誤差最小的全息圖所有像素值。直接算法主要有三類:直接搜索算法(Direct Search Algorithm)、模擬退火算法(Simulated Annealing Algorithm)以及遺傳算法(Genetic Algorithm)。
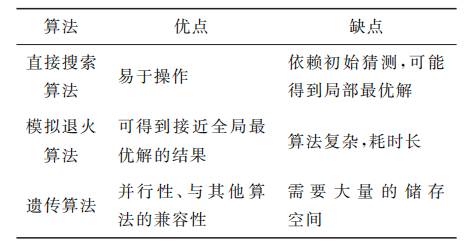
圖5 三種直接算法的比較
除以上介紹的算法外,論文中還介紹了近年來被提出的一系列算法,例如:介于迭代算法與非迭代算法兩種分類之間的純相位全息圖生成算法,該方法能夠節省大量計算時間,同時保持著較高的重建準確度,適合全息動態實時顯示等應用;以及近年來快速發展的深度學習方法也被用于全息圖壓縮以及生成,在循環中,CITL技術直接捕捉到全息圖的光學重建結果,并且將該結果用于對全息圖的進一步優化,并能夠取得較高的重建質量;還有由Chakravarthy等人提出的基于維爾丁格流(Wirtinger Flow)的相位提取方法可以將相位提取問題轉化為可用一階優化算法(First-Order Optimization Method)進行優化的二次問題(Quadratic Problem)。運用該相位提取方法進行全息圖優化可以使重建質量達到極高的準確度,而計算成本則僅與GS算法相當。目前,傳統的迭代與非迭代的純相位全息圖優化算法都已經取得了不錯的效果,但需要在計算耗時與重建質量間做出取舍,深度學習、維爾丁格流等新方法的不斷出現為解決這一問題帶來了新的思路,這些工作都有利于實時、廣視場、高質量全息三維顯示的早日實現。
審核編輯 黃宇
-
算法
+關注
關注
23文章
4615瀏覽量
92979 -
全息
+關注
關注
0文章
27瀏覽量
9361
發布評論請先 登錄
相關推薦

在純電感電路中正確的關系是什么
基于神經網絡的全息圖生成算法
全息投影呈現什么影像特征
全息投影運用了什么原理和技術
全息投影技術的原理是什么
全息投影空中成像原理是什么
神經網絡優化算法有哪些
激光全息無損檢測技術原理以及應用
無監督深度學習實現單次非相干全息3D成像

基于空間光調制器彩色全息顯示--上海瞬渺光電技術有限公司
純電容電路中電壓與電流的相位關系
面向3D增強現實(AR)眼鏡的波導全息顯示




 純相位全息圖優化算法綜述
純相位全息圖優化算法綜述










評論