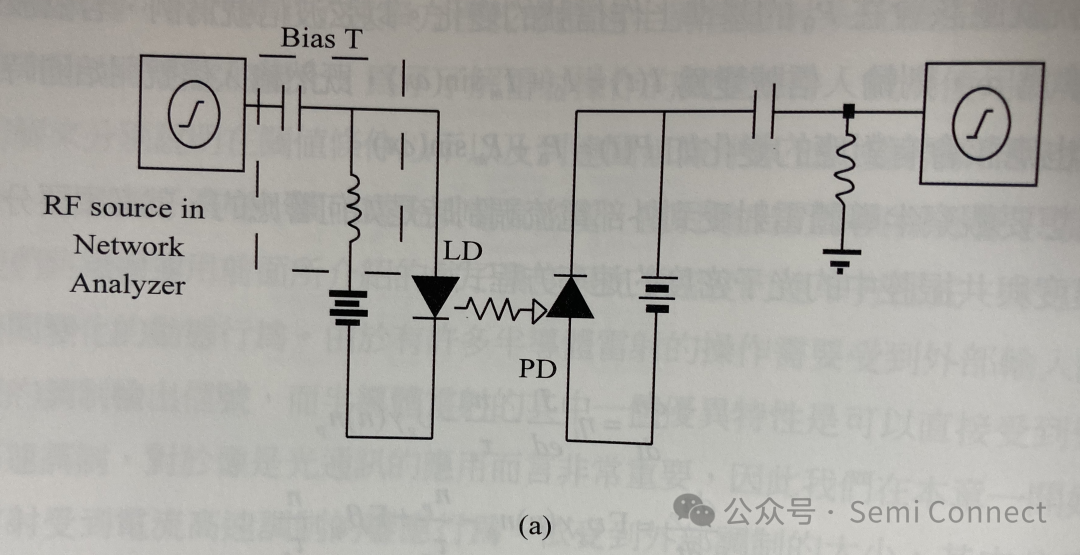
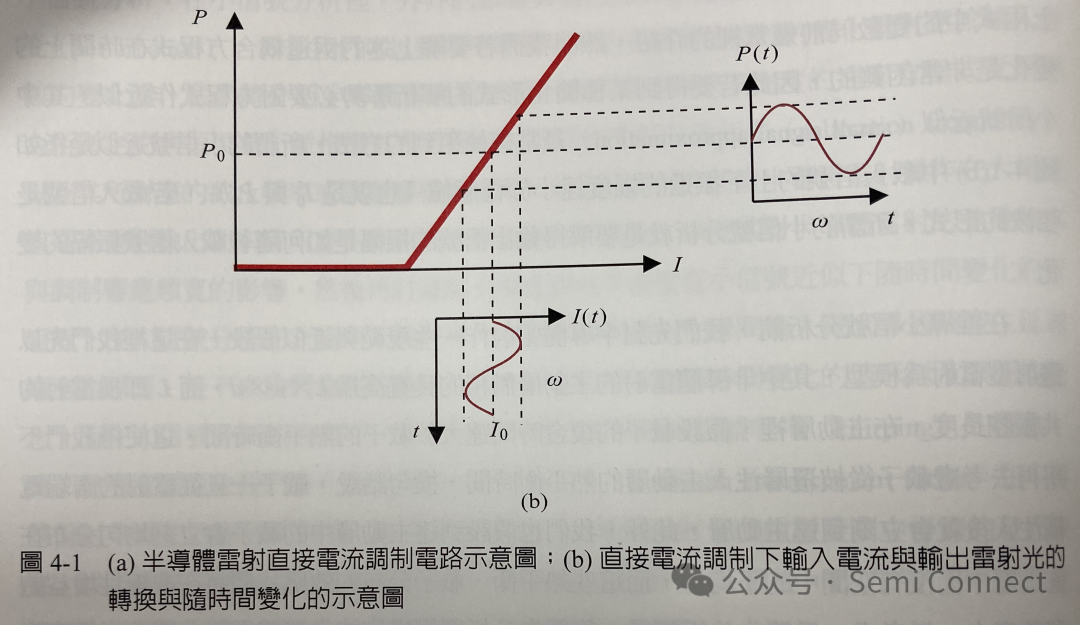
最常見的半導體雷射調制是如圖4-1的直接電流調制,半導體雷射偏壓操作在固定的電流值I0上,欲輸入的信號從網絡分析儀中產生經過Bias-T后加載到半導體雷射上,雷射的輸出信號就應該會在P0的基準上作信號的變化。以弦波信號為例,若弦波的振幅為Im,振蕩頻率為w,則輸入信號變為I(t)=I0+ImSin(wt),既然輸入信號開始隨時間變化,雷射光輸出也應該會有對應的變化如P(t)=P0+pmsin(wt)。
當我們想要觀察半導體雷射受到外部電流調制時是如何響應的,就必須要分析主動層中的載子濃度與共振腔中的光子密度的速率方程式:
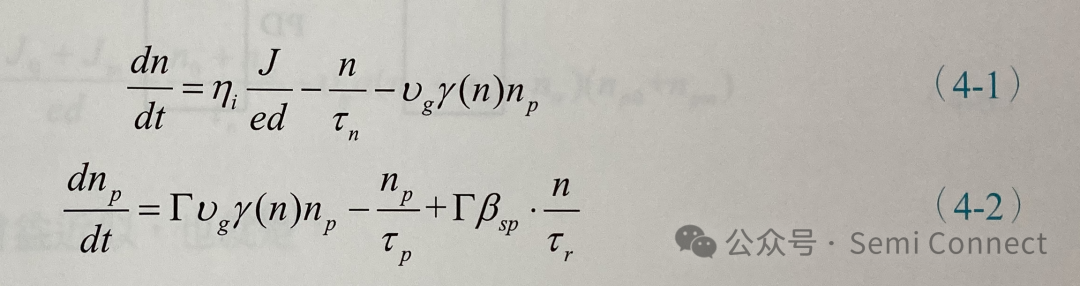
上兩式中的變數同前幾章里的介紹,然而我們若要解上述的兩道耦合方程式在時間上的變化是非常困難的,因此若要得到某種簡化形式的解析解勢必要對方程式作近似,其中小信號近似(small signal approximation)是常被使用到的方法,所謂的小信號近似是指如圖4-1(b)中載入信號的上下振蕩的幅度遠小于穩態值(也就是I0與P0),若載入信號是弦波的形式,所謂的小信號分析就是要解得輸出信號的振幅是如何隨著載入信號振幅的變化。
在推導小信號分析前,我們先對半導體雷射作一些規范與近似假設,在這里我們先以邊射型雷射為模型,其中半導體雷射的主動層體積的長寬高為LxWxd,而L即為雷射的共振腔長度,在主動層里,假設載子的復合時間遠大于載子的熱平衡時間,這使得我們不用再去考慮載子從披覆層注入主動層的熱平衡時間,換句話說,載子一旦從雷射的兩端電極注入后就會立刻到達主動層,此外,我們也假設到達主動層中的載子會立刻均勻分布在主動層中而沒有空間中的不均勻,而這些熱平衡、載子分布的效應我們將在非線性增益飽和效應中一并考慮;為簡化分析起見,我們先分析單模操作的半導體雷射,因此光子密度的速率方程式就只會有一道,此外,因為在邊射型雷射中自發放射因子βsp太小我們可先忽略不考慮。
因此在小信號分析的情況下,我們可以定義電流密度、載子濃度與光子密度隨時間的表示式:


我們假設Jo>Jm、n0>nm與np0>npm,其中下標0表示固定的穩態値,而下標m則表示小信號值。將上三式代入(4-1)式中并使用線性增益近似,即,我們可得:
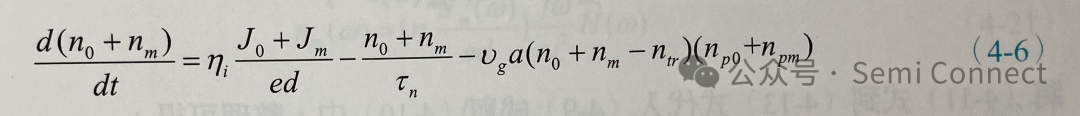
上式中我們使用了線性增益近似,也就是:
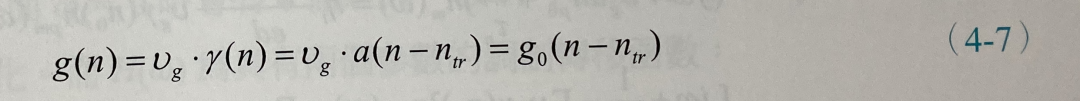
將(4-6)式展開,因為兩個小信號相乘的項nm?npm太小可以忽略不計,并將穩態項以及小信號項分別放在一起,可得:
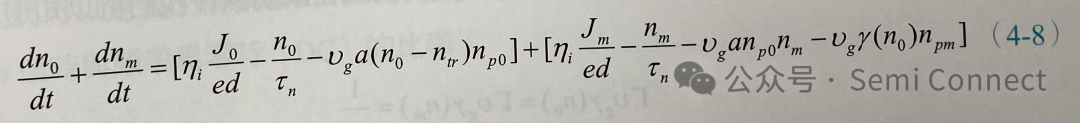
我們可以取出載子濃度小信號的變化為:?
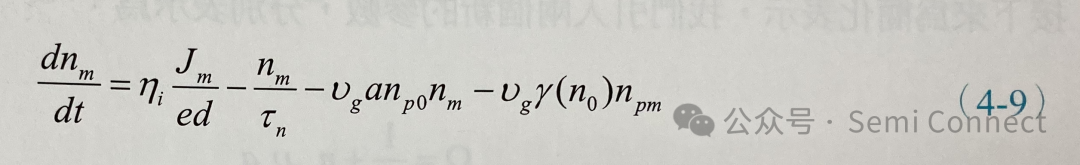
同樣的,對于計算光子密度小信號的變化,我們可以將(4-3)式到(4-5)式代入(4-2)式中,展開之后將兩個小信號相乘的項nm?npm=0,并將穩態項以及小信號項分放在一起,可得光子密度小信號的變化:???
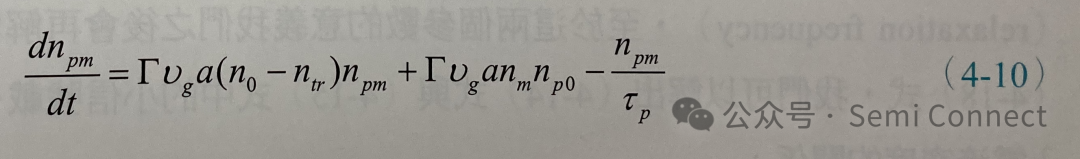
(4-9)式與(4-10)式即為載子濃度與光子密度的小信號速率方程式,我們可以發現,此二道方程式彼此之間又是互相耦合的。若小信號以弦波方式振蕩,則:
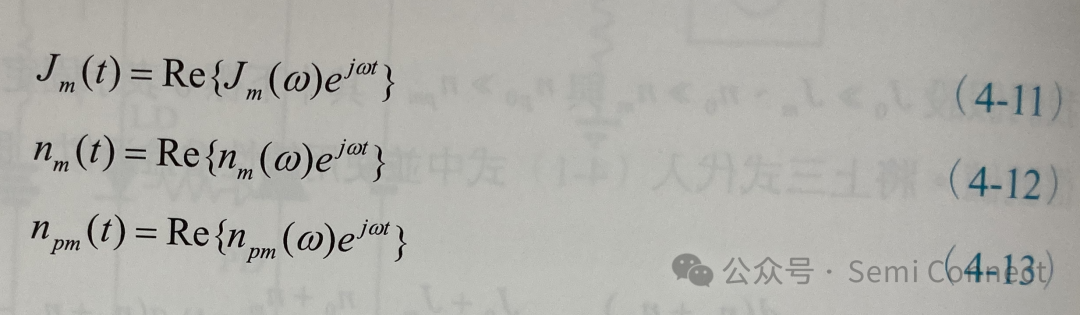
將(4-11)式到(4-13)式代入(4-9)式與(4-10)中,整理可得:
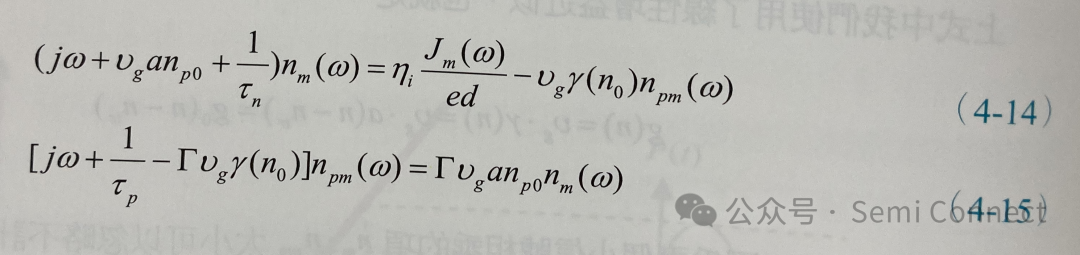
我們在前幾章介紹過當雷射操作在閾值條件以上時,盡管輸入電流改變,其載子濃度會被鉗制在nth,因此nth即為載子濃度的穩態值n0,因此從閾值條件我們可以知道:

接下來為簡化表示,我們引入兩個新的參數,分別表示為:
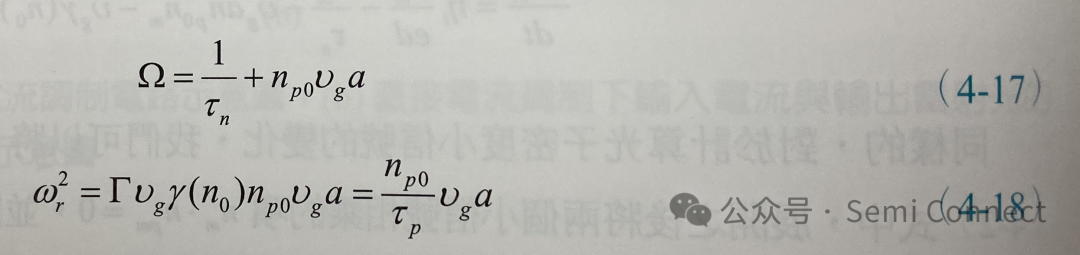
其中Ω被稱之為阻尼常數(damping constant)或衰減率,而Wr則被稱之為弛豫頻率(relaxation frequency),至于這兩個參數的意義我們之后會再解釋。使用(4-16)式到(4-18)式,我們可以解出(4-14)式與(4-15)式中的小信號載子濃度與光子密度對輸入電流密度的關系:
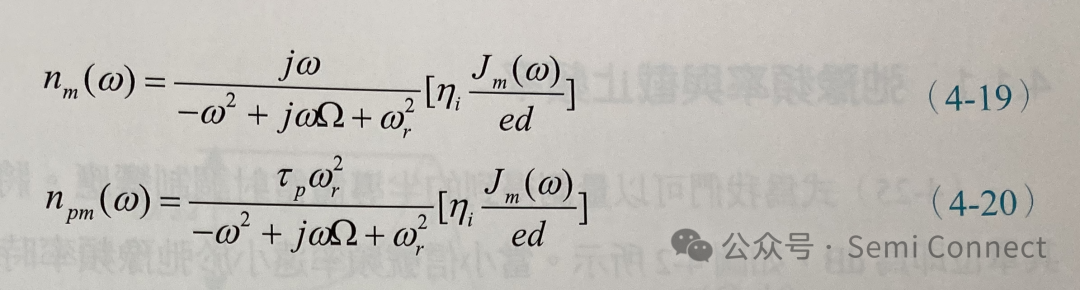
上式也可以整理成:
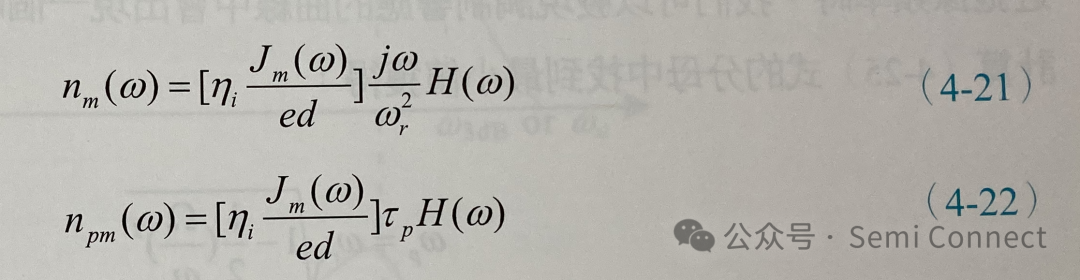
其中除了nm在復數平面w=0時會有0值之外,我們可以發現nm和npm主要都是隨著H(w)的頻率響應作變化。而H(w)為具有兩個參數的調制轉移函數:

我們可以定義小信號輸出的調制響應(modulation response)為小信號光子密度在頻率為w值時與頻率為零時(DC)的比率:
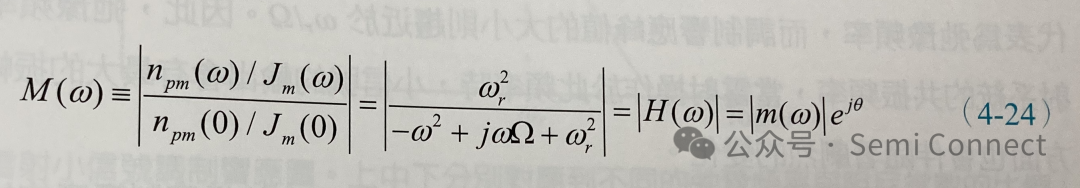
其中
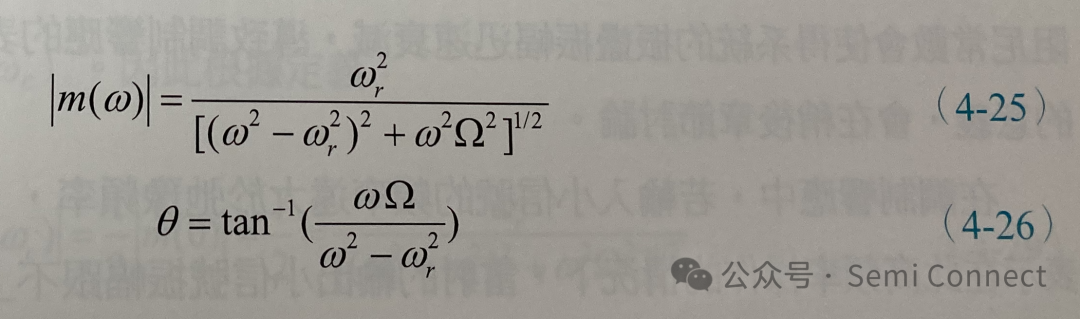
-
電流
+關注
關注
40文章
7116瀏覽量
134222 -
半導體
+關注
關注
335文章
28613瀏覽量
232774 -
小信號
+關注
關注
1文章
52瀏覽量
12350
原文標題:小信號響應
文章出處:【微信號:Semi Connect,微信公眾號:Semi Connect】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄


如何為波特圖設置頻率響應分析儀
DCDC電源負載瞬態響應分析

Moku:Lab頻率響應分析儀的應用指南
Moku:Lab頻率響應分析儀在阻抗測量中的應用
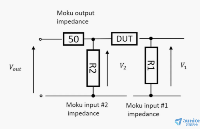
電源穩定性分析-Moku:Lab頻率響應分析儀應用指南



















評論