BCD代碼。Binary-Coded Decimal?,簡稱BCD,稱BCD碼或二轉十進制代碼,亦稱二進碼十進數。是一種二進制的數字編碼形式,用二進制編碼的十進制代碼。這種編碼形式利用了四個位元來儲存一個十進制的數碼,使二進制和十進制之間的轉換得以快捷的進行。這種編碼技巧,最常用于會計系統的設計里,因為會計制度經常需要對很長的數字串作準確的計算。相對于一般的浮點式記數法,采用BCD碼,既可保存數值的精確度,又可免卻使電腦作浮點運算時所耗費的時間。此外,對于其他需要高精確度的計算,BCD編碼亦很常用。
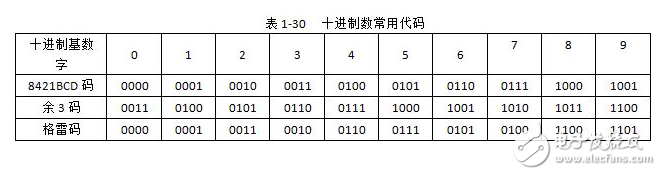
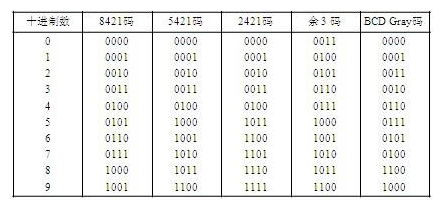
由于十進制數共有0、1、2、……、9十個數碼,因此,至少需要4位二進制碼來表示1位十進制數。4位二進制碼共有2^4=16種碼組,在這16種代碼中,可以任選10種來表示10個十進制數碼,共有N=16!/(16-10)!約等于2.9乘以10的10次方種方案。常用的BCD代碼列于末。
BCD碼的運算法則
BCD碼的運算規則:BCD碼是十進制數,而運算器對數據做加減運算時,都是按二進制運算規則進行處理的。這樣,當將 BCD碼傳送給運算器進行運算時,其結果需要修正。
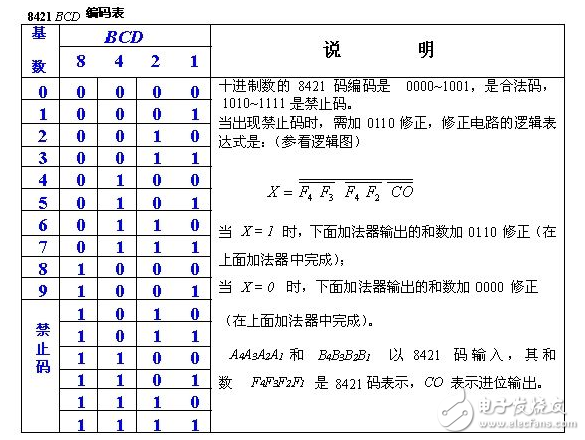
修正的規則是:當兩個BCD碼相加,如果和等于或小于 1001(即十進制數 9),不需要修正;如果相加之和在 1010 到1111(即十六進制數 0AH~0FH)之間,則需加 6 進行修正;如果相加時,本位產生了進位,也需加 6 進行修正。這樣做的原因是,機器按二進制相加,所以 4 位二進制數相加時,是按“逢十六進一”的原則進行運算的,而實質上是 2 個十進制數相加,應該按“逢十進一”的原則相加,16 與10相差 6,所以當和超過 9或有進位時,都要加 6 進行修正。下面舉例說明。
需要修正 BCD碼運算值的舉例。
(1) 計算 5+8;
(2) 計算 8+8
解:(1) 將 5 和 8 以 8421 BCD輸入機器,則運算如下:
0 1 0 1
+) 1 0 0 0
1 1 0 1 結果大于 9
+) 0 1 1 0 加 6 修正
1 0 0 1 1 13 的 BCD碼
結果是 0011,即十進制數 3,還產生了進位。5+8=13,結論正確。
(2)將8以8421 BCD輸入機器,則運算如下:
1 0 0 0
+)1 0 0 0
1 0 0 0 0 結果大于9
+)0 1 1 0 加6修正
1 0 1 1 0 16的BCD碼
結果是0110,即十進制的6,而且產生進位。8+8=16,結論正確。
微機原理代碼: (AL=BCD 5,BL=BCD 8) 設AH=0,則
ADD AL,BL
AAA
結果為 AX=0104H,表示非壓縮十進制數,CF=1,AF=1,AH=1,AL=1
使用AAA指令,可以不用屏蔽高半字節,只要在相加后立即執行AAA指令,便能在AX中得到一個正確的非壓縮十進制數
壓縮BCD碼與非壓縮BCD碼的區別—— 壓縮BCD碼的每一位用4位二進制表示,一個字節表示兩位十進制數。例如10010110B表示十進制數96D;非壓縮BCD碼用1個字節表示一位十進制數,高四位總是0000,低4位的0000~1001表示0~9.例如00001000B表示十進制數8.
-
十進制
+關注
關注
0文章
67瀏覽量
13208 -
BCD碼
+關注
關注
1文章
52瀏覽量
18292 -
8421碼
+關注
關注
1文章
8瀏覽量
4041
發布評論請先 登錄
相關推薦
常用編碼(BCD編碼、余3碼、格雷反射碼、奇偶校驗碼)
什么是BCD碼、8421碼、余三碼、格雷碼
quartusii 的warning和仿真問題
【FPGA開源教程連載】第五章 BCD計數器設計與應用
想用兩片74LS153和一只數碼顯示四組8421BCD碼測試系統即用一只數碼管分別顯示四位十進制數的個位 十位 百位 千位
C語言中十進制轉8421BCD碼是用的什么方法?
8421BCD碼與二進制原碼的相互轉換
在FPGA中實現一種二進制轉BCD碼的電路設計
常用編碼(BCD編碼、余3碼、格雷反射碼、奇偶校驗碼)
8421bcd碼轉換二進制
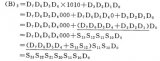
余3碼至8421BCD碼的轉換_8421BCD碼轉換成余3碼
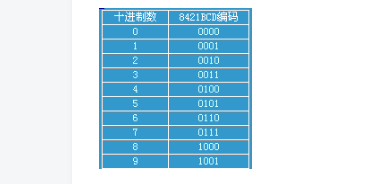




 8421bcd碼運算規則
8421bcd碼運算規則











評論