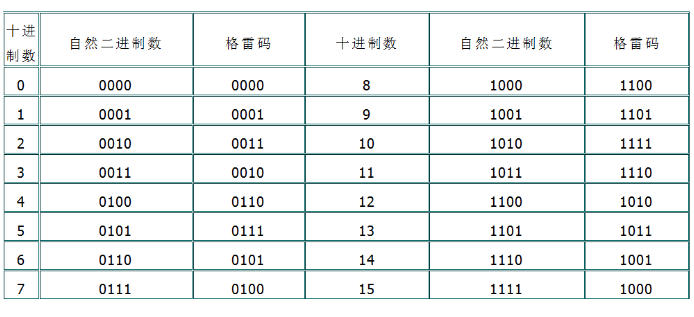
格雷碼
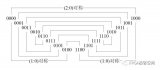
在一組數的編碼中,若任意兩個相鄰的代碼只有一位二進制數不同,則稱這種編碼為格雷碼(Gray Code),另外由于最大數與最小數之間也僅一位數不同,即“首尾相連”,因此又稱循環碼或反射碼。在數字系統中,常要求代碼按一定順序變化。例如,按自然數遞增計數,若采用8421碼,則數0111變到1000時四位均要變化,而在實際電路中,4位的變化不可能絕對同時發生,則計數中可能出現短暫的其它代碼(1100、1111等)。在特定情況下可能導致電路狀態錯誤或輸入錯誤。使用格雷碼可以避免這種錯誤。格雷碼有多種編碼形式。
格雷碼(Gray Code)曾用過Grey Code、葛萊碼、格萊碼、戈萊碼、循環碼、反射二進制碼、最小差錯碼等名字,它們有的不對,有的易與其它名稱混淆,建議不要再使用這些曾用名。
二進制
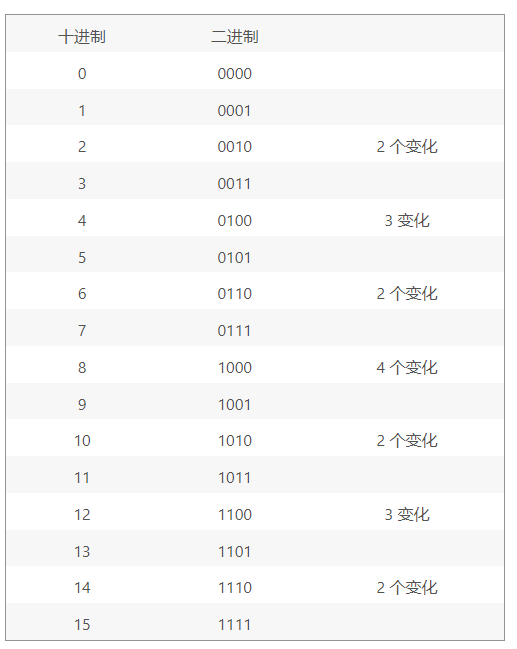
二進制是計算技術中廣泛采用的一種數制。二進制數據是用0和1兩個數碼來表示的數。它的基數為2,進位規則是“逢二進一”,借位規則是“借一當二”,由18世紀德國數理哲學大師萊布尼茲發現。當前的計算機系統使用的基本上是二進制系統,數據在計算機中主要是以補碼的形式存儲的。計算機中的二進制則是一個非常微小的開關,用“開”來表示1,“關”來表示0。
20世紀被稱作第三次科技革命的重要標志之一的計算機的發明與應用,因為數字計算機只能識別和處理由‘0’。‘1’符號串組成的代碼。其運算模式正是二進制。19世紀愛爾蘭邏輯學家喬治布爾對邏輯命題的思考過程轉化為對符號“0‘’。‘’1‘’的某種代數演算,二進制是逢2進位的進位制。0、1是基本算符。因為它只使用0、1兩個數字符號,非常簡單方便,易于用電子方式實現。

二進制轉格雷碼公式
十進制 586 = 二進制 1001001010 = 格雷碼 1101101111。
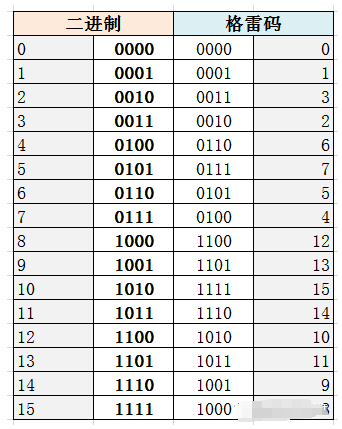
二進制碼 ----》 格雷碼(編碼):
從最右邊一位起,依次將每一位與左邊一位異或(XOR),作為對應格雷碼該位的值,最左邊一位不變(相當于左邊是0)。
格雷碼的是特點是:
相鄰兩數的格雷碼,僅僅有一位二進制發生變化。
而且在其范圍內的最小值和最大值,也僅僅有一位二進制發生變化。
例如下面兩數:
最小:二進制0000=格雷碼0000
最大:二進制1111=格雷碼1000
看到了吧,0000 和 1000,僅僅有一位數發生變化。
-------
如果在變換的過程中,先把十進制轉換成BCD碼,這就失去了格雷碼的特點。
因為在BCD碼中:
最小:二進制0000=格雷碼0000
最大:二進制1001=格雷碼1101
可以看出,它們之間有三位發生變化。
通過BCD碼來變換格雷碼,思路不對。變換出來的,并不是原數的格雷碼。
自然二進制數轉換到格雷碼
------------
設有 N 位二進制數 B(i),其中 0 《= i 《= N - 1;它可以變換成為同樣位數的格雷碼 G(i)。
二進制數與格雷碼的轉換公式如下:
G(i) = B(i+1) XOR B(i) ; 0 《= i 《 N - 1
G(i) = B(i) ; i = N - 1
如果是通過編程計算進行變換,就需要使用這個公式逐位的計算;
如果是使用硬件電路進行變換,就可以使用做而論道前面在回答問題時給出的電路。
格雷碼轉換到自然二進制數
------------
設有 N 位格雷碼 G(i),把它轉換成自然二進制數的算法如下。
自然二進制碼的最高位等于雷碼的最高位;
自然二進制碼的次高位為最高位自然二進制碼與次高位格雷碼相異或;
自然二進制碼的其余各位與次高位自然二進制碼的求法相類似。
轉換公式如下:
B(i) = G(i) ; i = N - 1
B(i) = B(i+1) XOR G(i) ; 0 《= i 《 N - 1
-
二進制
+關注
關注
2文章
795瀏覽量
41643 -
格雷碼
+關注
關注
2文章
34瀏覽量
13185
發布評論請先 登錄
相關推薦




 二進制轉格雷碼公式
二進制轉格雷碼公式












評論