為了保證通信過程中數據傳輸的正確性和完整性,并且在通信過程中,如果數據傳輸發生一位錯誤,能夠將其矯正過來,將信息數據進行漢明編碼后再進行數據傳輸。
漢明碼(Hamming Code)也叫海明碼,是Richard Hamming(貝爾實驗室)于1950年發明的,漢明碼也是利用了奇偶校驗位概念,通過在數據位后增加一些比特以驗證數據的有效性,故漢明碼也屬于線性糾錯碼(可糾錯1-bit錯誤檢出2-bit錯誤)。漢明碼無法實現2位及2位以上糾錯。
漢明碼原理
漢明碼運算需要構造G生成矩***和H監督矩***,關于構造方法可參考相關計算機原理書籍,這里只需了解些簡單的概念即可。
設數據位數為m,校驗位數為k,則總編碼位數為n,所以,n=m+k,則,
有Hamming不等式:
2^k-1》=n
也可表示為:2^k》=m+k+1,該不等式用于對比運算計算數據位數和檢驗位數,舉個例子假設數據位為64,那么校驗位則為(“2^k-k》=65” =》k=7)。
校驗位數一般指最小值,因為k越小總信息位會越小,傳輸開銷自然越小。
信息位數一般指最大值,但由于2^k-k只能在固定的離散值里取值,所以信息位也可能不是最大值,比如信息位為24,計算需要校驗位5,但同樣可信息位為25時,校驗位同樣是5。
校驗位數VS信息位數關系如下表:
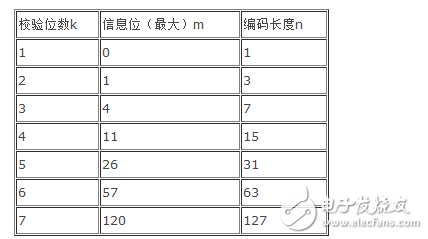
注:漢明碼的特性決定,一般不會做太多信息位的校驗,信息位越長出現多余兩個錯誤的概率會越高,這將帶來糾錯的難度。
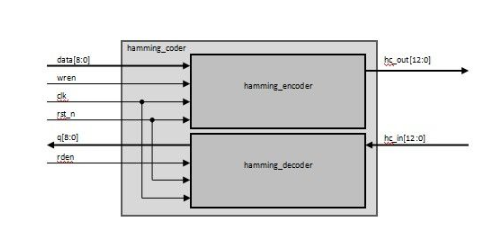
漢明碼編碼原理
設碼長為n,信息位長度為k,監督位長度為r=n-k。如果需要糾正一位出錯,因為長度為n的序列上每一位都可能出錯,一共有n種情況,另外還有不出錯的情況,所以我們必須用長度為r的監督碼表示出n+1種情況。而長度為r的監督碼一共可以表示2^r種情況 。因此
2^r 》= n + 1, 即r 》= log(n+1)
我們以一個例子來說明漢明碼。假設k=4,需要糾正一位錯誤,則
2^r 》= n + 1 = k + r + 1 = 4 + r + 1
解得r 》= 3。我們取r=3,則碼長為3+4=7。用a6,a5,。。.a0表示這7個碼元。用S1,S2,S3表示三個監關系式中的校正子。我們作如下規定(這個規定是任意的):
S1 S2 S3 錯碼的位置
0 0 1 a0
0 1 0 a1
1 0 0 a2
0 1 1 a3
1 0 1 a4
1 1 0 a5
1 1 1 a6
0 0 0 無錯
按照表中的規定可知,僅當一個錯碼位置在a2,a4,a5或a6時校正子S1為1,否則S1為0。這就意味著a2,a4,a5,a6四個碼元構成偶校驗關系:
S1 = a6⊕a5⊕a4⊕a2 (1)式
同理,可以得到:
S2 = a6⊕a5⊕a3⊕a1 (2)式
S3 = a6⊕a4⊕a3⊕a0 (3)式
在發送信號時,信息位a6,a5,a4,a3的值取決于輸入信號,是隨機的。監督為a2,a1,a0應該根據信息位的取值按照監督關系決定,即監督位的取值應該使上述(1)(2)(3)式中的S1,S2,S3為0,這表示初始情況下沒有錯碼。即
a6⊕a5⊕a4⊕a2 = 0
a6⊕a5⊕a3⊕a1 = 0
a6⊕a4⊕a3⊕a0 = 0
由上式進行移項運算,得到:
a2 = a6⊕a5⊕a4
a1 = a6⊕a5⊕a3
a0 = a6⊕a4⊕a3
已知信息位后,根據上式即可計算出a2,a1,a0三個監督位的值。
接收端受到每個碼組后,先按照(1)~(3)式計算出S1,S2,S3,然后查表可知錯碼情況。
例如,若接收到的碼字為0000011,按照(1)~(3)計算得到:
S1 = 0, S2 = 1, S3 = 1
查表可得在a3位有一個錯碼。
這種編碼方法的最小漢明距離為d=3,所以這種編碼可以糾正一個錯碼或者檢測兩個錯碼。
漢明碼實例
下文示例為(30,24)漢明碼計算方法,用在MIPI DSI包頭部分(MIPI Alliance Specification for Display Serial Interface,Chapter 9),DSI包頭格式固定為24bits Data+8bits ECC,8bitsECC中預設P6=P7=0,所以實際n=30,m=24,k=6。
檢驗位計算方法參考MIPI DSI table22生成矩***(Px vs [DataBit0~DataBitx]),比如P5=D10^D11^.。。.D23,表示對應DataBit23的P5列,只有這些DataBit位為1。
int main() {
char res;
char in[20]={0};
char D0,D1,D2,D3,D4,D5,D6,D7,D8,D9,D10,D11,D12,D13,D14,D15,D16,D17,D18,D19,D20,D21,D22,D23;
char P0,P1,P2,P3,P4,P5,P6,P7;
cout《《“Checking Codes(eg.0x1234AF, \”-\“ for exit): 0x”;
cin》》in;
if(in[0]==‘-’) {
return 0;
}
for(int i=0;i《6;i++){
if((in[i]》=‘0’) && (in[i]《=‘9’)) {
in[i] = in[i]-0x30;
}else if((in[i]》=‘A’) && (in[i]《=‘F’)){
in[i] = in[i]-‘A’+10;
}else {
return 0;
}
}
D0=in[1]&0x01; D1=(in[1]&0x02)》》1;
D2=(in[1]&0x04)》》2; D3=(in[1]&0x08)》》3;
D4=in[0]&0x01; D5=(in[0]&0x02)》》1;
D6=(in[0]&0x04)》》2; D7=(in[0]&0x08)》》3;
D8=in[3]&0x01; D9=(in[3]&0x02)》》1;
D10=(in[3]&0x04)》》2; D11=(in[3]&0x08)》》3;
D12=in[2]&0x01; D13=(in[2]&0x02)》》1;
D14=(in[2]&0x04)》》2; D15=(in[2]&0x08)》》3;
D16=in[5]&0x01; D17=(in[5]&0x02)》》1;
D18=(in[5]&0x04)》》2; D19=(in[5]&0x08)》》3;
D20=in[4]&0x01; D21=(in[4]&0x02)》》1;
D22=(in[4]&0x04)》》2; D23=(in[4]&0x08)》》3;
P7=0;
P6=0;
P5=D10^D11^D12^D13^D14^D15^D16^D17^D18^D19^D21^D22^D23;
P4=D4^D5^D6^D7^D8^D9^D16^D17^D18^D19^D20^D22^D23;
P3=D1^D2^D3^D7^D8^D9^D13^D14^D15^D19^D20^D21^D23;
P2=D0^D2^D3^D5^D6^D9^D11^D12^D15^D18^D20^D21^D22;
P1=D0^D1^D3^D4^D6^D8^D10^D12^D14^D17^D20^D21^D22^D23;
P0=D0^D1^D2^D4^D5^D7^D10^D11^D13^D16^D20^D21^D22^D23;
res = ((P7&0x01)*8+(P6&0x01)*4+(P5&0x01)*2+(P4&0x01))*16+(P3&0x01)*8+(P2&0x01)*4+(P1&0x01)*2+(P0&0x01);
printf(“Result:0x%02X\r\n”,res);
return 0;
}
-
漢明碼
+關注
關注
0文章
8瀏覽量
8075
發布評論請先 登錄
相關推薦
實現漢明糾錯碼的編碼和解碼方案設計

基于FPGA的交織編碼技術研究及實現
基于FPGA的漢明碼譯碼器如何對碼元數據添加噪聲干擾?
【原創】基于FPGA的漢明碼編碼解碼設計
提高漢明碼對突發干擾的糾錯能力
PIC單片機串行通信中的漢明編碼自動檢糾錯
一種基于漢明碼和濕紙碼的隱寫算法
漢明碼計算及其糾錯原理詳解
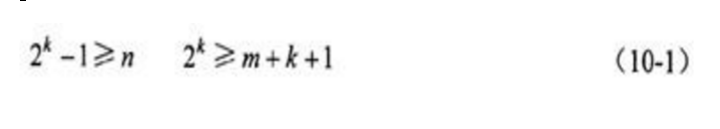




 漢明碼編碼原理介紹
漢明碼編碼原理介紹












評論