在計算機科學的領域,排序算法是每位學生必學的基礎,而排序的需求是每位程序員在編程過程中都會遇到的。
在你輕松調用 .sort() 方法對數據進行排序時,是否曾好奇過,這個簡單的方法背后使用的是哪種排序算法呢?
本文將帶你走進 TimSort,一個在標準函數庫中廣泛使用的排序算法。
這個算法由工程師 Tim Peters 于 2001 年專為 Python 設計,并自 Python 2.3 版本起成為其默認排序算法。它的影響不止于此,Java、Android、GNU Octave、Chrome 的 V8 引擎、Swift 以及 Rust 等也紛紛采用了這一算法。
那么,是什么讓 TimSort 在眾多排序算法中獨樹一幟,贏得了如此廣泛的應用和認可呢?
在本文中,我們將深入剖析 TimSort 的內部機制,揭示其背后的高效實現原理,讓你領略這一算法的獨特魅力。
小規模數據的高效處理:插入排序
TimSort 是一個結合了插入排序和歸并排序的混合排序算法,特別適合處理真實世界的各種數據。
從這句定義中您可能會好奇,為什么 TimSort 選擇了插入排序和歸并排序?為什么說它適合處理真實世界的數據?
讓我們首先探討第一個問題,為什么插入排序成為了 TimSort 的關鍵組成部分。
盡管插入排序的理論時間復雜度為 O(n^2),看似不及 O(nlogn) 的高效排序算法,但插入排序的實際效率卻非常高效,尤其是在處理小規模數據集時。
這是因為插入排序只涉及兩個簡單操作:比較和移動。
通過比較,我們能夠確定新元素的插入點;通過移動,我們為新元素的插入騰出空間。
視頻 插入排序
關鍵在于,對于小數據集而言,n^2 與 nlogn 的差異并不顯著,復雜度不占主導作用,此時每輪單元的操作數量才起到決定性因素。得益于其簡潔的操作,插入排序在小規模數據集上的表現通常非常出色。
但究竟什么規模的數據集算是“小”呢?
以 Python 為例,當數據集大小小于 64 時,它會默認采用插入排序。而在 Java 中,這一界限則被設定在了 32。
插入排序的優化:二分插入排序
對于 TimSort 算法來說,傳統插入排序也存在進一步提升性能的空間。
回顧一下,插入排序涉及的關鍵操作有兩個:比較和移動。這其中,對于一個數組來說,移動的總次數是固定不變的,因此,我們可以嘗試從減少比較的次數來優化。
在插入排序的執行過程中,數據被劃分為已排序和未排序的兩個部分。在已排序部分,我們尋找未排序部分下一個元素的插入位置時,常規做法是采用線性查找。
但 TimSort 采用了更高效的策略——二分查找法。利用二分查找在已排序部分尋找插入點,大幅減少了比較次數。
對小規模數據集而言,這種優化尤其有效,能顯著提升排序的效率。
視頻 二分查找插入位置
舉個例子,如上面視頻所示,在使用傳統插入排序時,為將元素 2 插入正確位置,需要進行 5 次比較。而在二分插入排序中,這一過程可以縮減至僅需 2 次比較,從而顯著提高排序效率。
TimSort 的工作原理
在詳細了解了插入排序在 TimSort 中的作用之后,接下來我們可以進一步了解歸并排序在 TimSort 中的應用。不過在這之前,我們需要知道 TimSort 的整體工作原理。
TimSort 的設計目標是最大限度地利用在絕大多數實際數據中已經存在的連續有序序列,這些被稱為自然序列 natural run。
在算法的執行過程中,它遍歷數據集,借助于這些自然序列,必要時將附近的元素添加進去,形成一個個的數據塊 run,其中每個 run 中的元素都會進行排序。
隨后,這些有序的 run 被堆疊在一個棧中,形成了算法處理過程的一個關鍵結構。
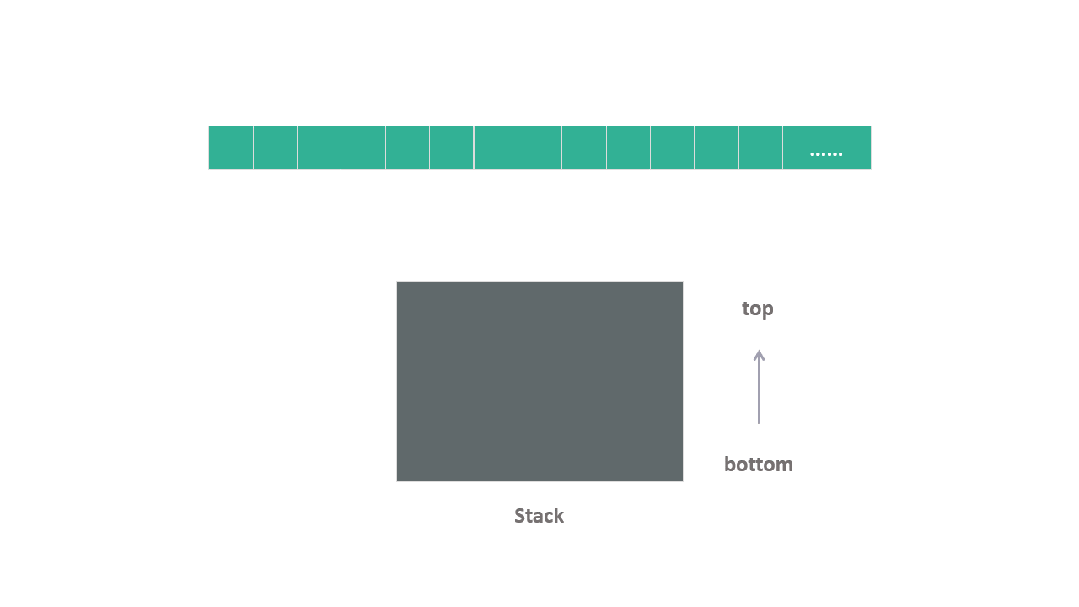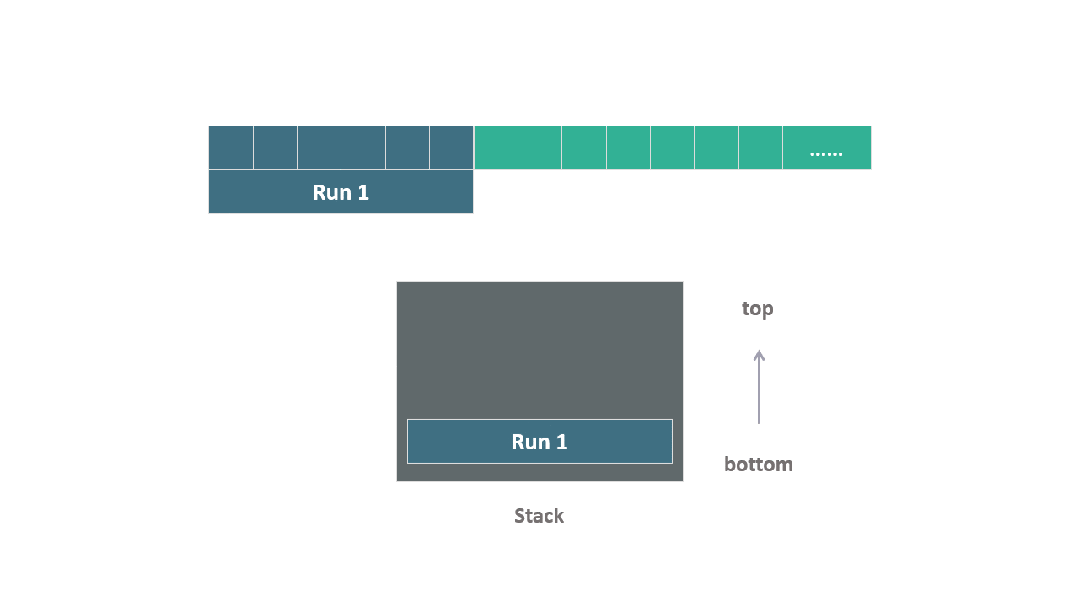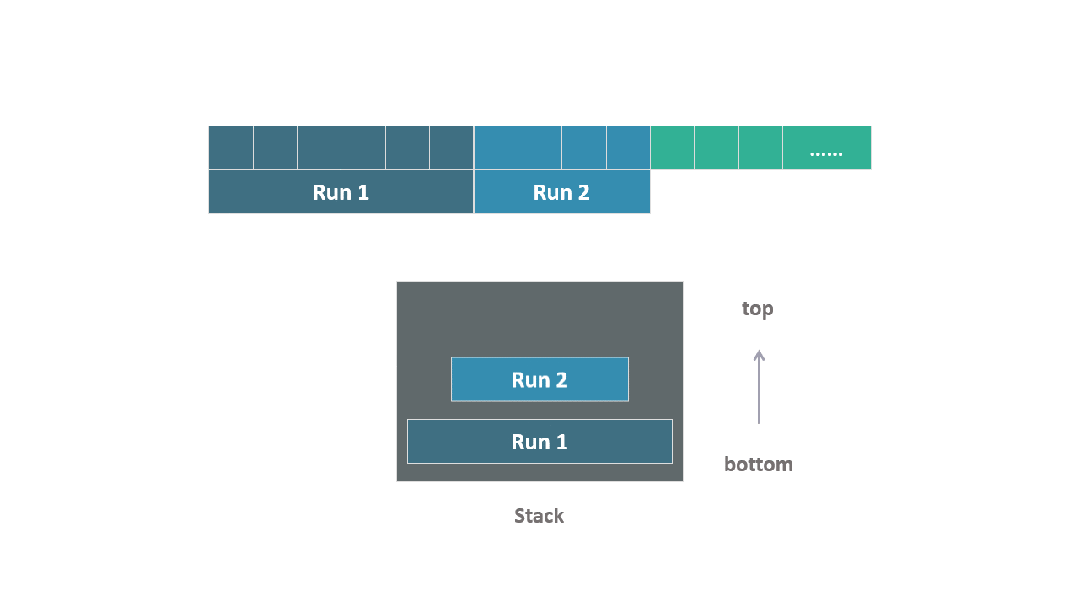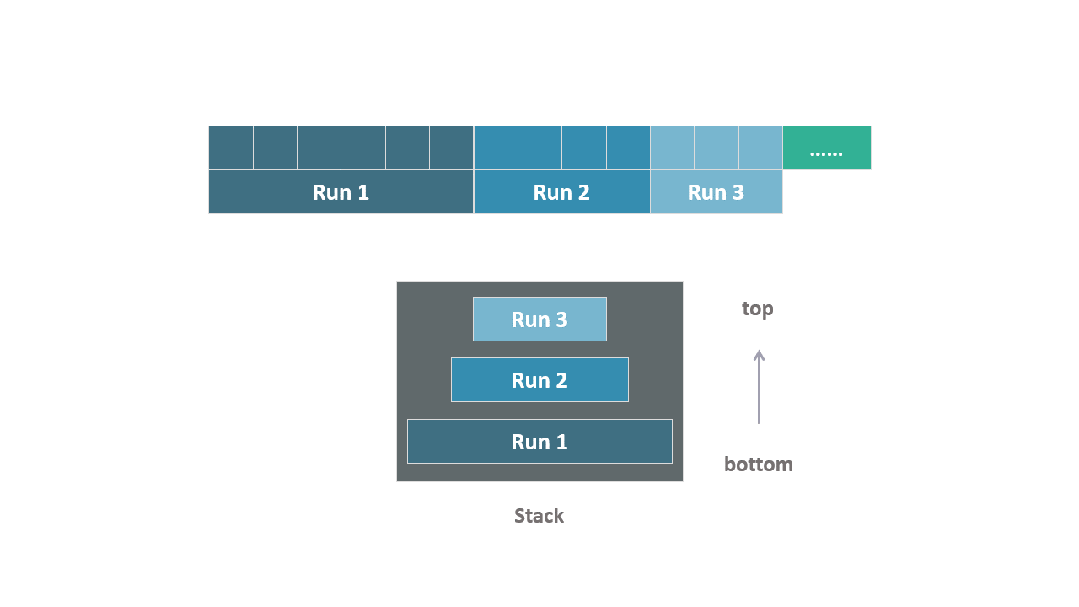
動圖 run 堆疊
當一個新的 run 被識別并加入到棧中后,TimSort 會根據棧頂多個 run 的長度來判斷,是否應該合并棧頂附近的 run。
這個過程將持續進行,直到所有數據都遍歷完。
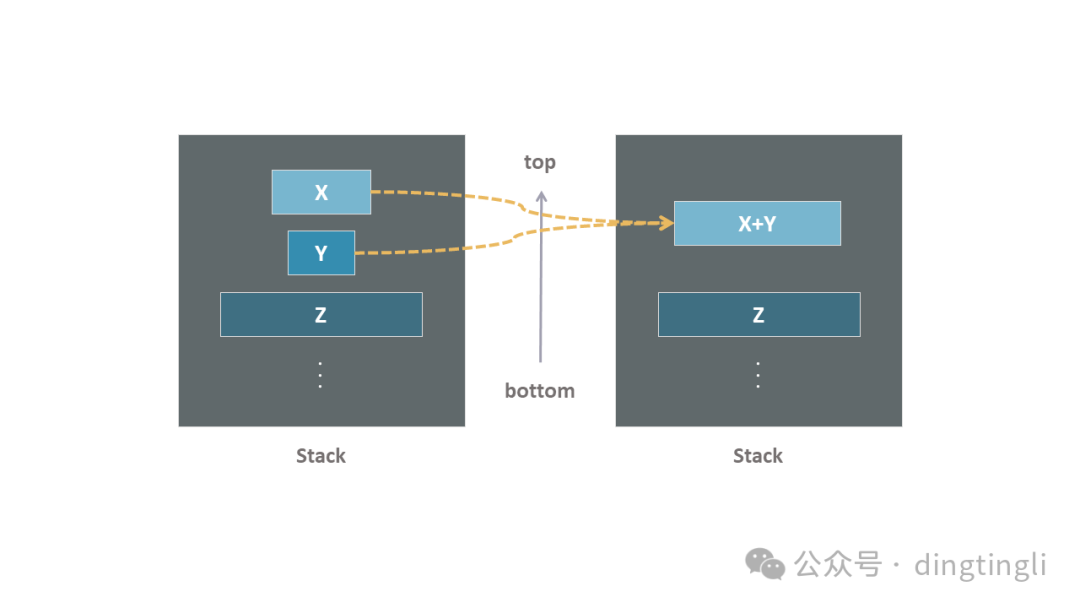
run 合并
遍歷結束后,棧中剩余的所有 run 每次兩兩合并,直到最終形成一個完整有序的 run。
相比傳統歸并排序,合并預排序的 run 會大大減少了所需的比較次數,從而提升了整體的排序效率。
現在,你可能對 TimSort 算法的細節產生了許多疑問。run 是如何形成的?這些 run 是如何利用數據中已存在的自然序列?當 run 被加入到棧中后,依據什么規則來決定是否合并?……
不用擔心,接下來我們將逐一解答這些問題,帶你更深入地理解 TimSort 算法。
計算 minrun
在 TimSort 算法中,run 的生成非常關鍵,而這一過程的核心是確定 run 最小長度 minrun。這個長度的設定是為了在排序過程中達到兩個關鍵目標:
確保 run 足夠長,以便有效地利用歸并排序;
避免 run 過于長,從而在合并時仍能保持高效。
實驗研究表明,當 minrun 小于 8 時,第一條原則難以滿足;而當 minrun 超過 256 時,第二條原則受到影響。
因此,最佳的 minrun 長度范圍被確定在 32 到 64 之間。
這個范圍與我們之前提到的插入排序中小規模數據集的長度范圍非常接近,這并非巧合。事實上,Timsort 在生成 run 時也會利用到插入排序。
具體計算 minrun 的方法如下:
目標:選取一個 minrun 值,以使長度為 n 的數組被分割成約 n/minrun 個 runs,每個 run 包含大約 32 到 64 個元素。
計算方法:選擇最接近 n/(2^k) 的 minrun 值,這里 k 是使 n/(2^k) 落在32至64之間的最大整數。然后設置 minrun 為 n/(2^k)。
例如,對于長度為 65 的數組,minrun 將設置為33,形成 2 個runs;對于長度為 165 的數組,minrun 設置為42,形成 4 個runs。
這個計算過程涉及到 (2^k),可以通過位移操作高效實現:
defget_minrun(n): #用于記錄在不斷右移過程中,n的最低位上非零位的數量 r=0 whilen>=64: #檢查n的最低位是否為1,若是,則設置r為1 r|=n&1 #向右移動一位,相當于n除以2 n>>=1 #返回n加上r,n是原始值的最高6位,r是表示過程中n是否有非零最低位的標志 returnn+r
這種方法不僅保證了 minrun 的有效性,而且利用了位運算的高效性,體現了 TimSort 設計的巧思。
run 的生成過程
在掌握了 minrun 的計算方法之后,我們現在可以探究 run 是如何生成的。
TimSort 的核心目標是充分利用數據中已存在的連續有序序列來生成 run,但這是如何實現的呢?
TimSort 的處理流程可分為以下幾個關鍵步驟:
TimSort 開始掃描整個數組,尋找連續的升序或降序序列。
如果遇到升序部分,TimSort 會持續掃描直到升序結束。
如果遇到降序部分,TimSort 會繼續掃描直到降序結束,并隨后將這部分翻轉成升序。
如果上述步驟識別的 run 未達到 minrun 長度,TimSort 會繼續擴展這個 run,向數組后方遍歷,納入更多元素,直至達 minrun 長度。在這個階段,新加入元素的順序并不重要。
一旦擴展完成,這個擴展后的 run(無論其最初是否有序)都將通過插入排序進行排序,以確保其內部有序。
如果識別的 run 長度遠超 minrun,對于這些較長的連續有序序列,TimSort 會保持其原始長度,不進行切割。這是因為較長的有序序列對于減少后續合并操作的復雜度非常有利。
對于這些超長的 run,通常無需進行額外排序,除非它們是降序,這時 TimSort 會先將其翻轉成升序。
通過這些策略,TimSort 能夠高效地生成一個有序的、長度至少為 minrun 的 run,為后續的歸并排序過程奠定了堅實基礎。
棧中 run 的合并規則
在 TimSort 算法中,每生成一個新的 run,它就會被加入到一個專門的棧中。
這時,TimSort 會對棧頂的三個 run(我們稱它們為X、Y和Z)進行檢查,以確保它們符合特定的合并規則:
|Z| > |Y| + |X|
|Y| > |X|
如果這些條件沒有被滿足,Y 就會與 X 或 Z 中較小的一個合并,并重新檢查上述條件。當所有條件都滿足時,可以在數據中繼續遍歷生成新的 run。

run 合并
這種獨特的合并規則是為了實現什么目標呢?
在 TimSort 的合并規則下,最終保留在棧中的每個 run 的長度至少等于前兩個 run 的總長度(由于滿足|Z| > |Y| + |X| 和 |Y| > |X|的規則)。
這種設計意味著,隨著時間的推移,棧中 run 的長度會逐漸增大,其增長方式類似于斐波那契數列。
這種增長模式的一個重要優勢在于,它提供了一種有效的方式來平衡數據遍歷完成之后 run 的合并操作,同時避免了過于頻繁的合并。
在最理想情況下,這個棧從頂部到底部 run 的長度應該是[2,2,4,8,16,32,64,...]。這樣,從棧頂到棧底的合并過程中,每次合并的兩個 run 的長度都是相等的,形成了完美的合并。

棧中 run 最理想形態
通過這些巧妙的規則,TimSort 在保證合并操作近似均衡的同時,也確保了在追求均衡和簡化合并決策之間的權衡。
正如 Tim Peters 所指出的,找到一種方式來維持棧中這兩個規則,是一個極具智慧的折中選擇。
合并過程中的空間開銷
了解完 TimSort 的工作原理和 run 在棧中的合并規則之后,我們現在來看 TimSort 中的最后一個重要環節:如何高效地運用歸并排序?
雖然傳統的歸并排序也擁有 O(nlogn) 的時間復雜度,但它并不是原地排序,并且需要額外的 O(n) 空間開銷,這使得它并沒有被廣泛地運用。
當然,也有改良過的原地歸并排序的實現,但它們的時間開銷就會比較大。為了在效率和空間節約之間取得平衡,TimSort 采用了一種改進的歸并排序,其空間開銷遠小于O(n)。
以一個具體例子來說明:假設我們有兩個已排序的數組 [1, 2, 3, 6, 10] 和 [4, 5, 7, 9, 12, 14, 17],目標是將它們合并。
在這個例子中,我們可以觀察到:
第二個數組中的最小元素(4)需要插入到第一個數組的第四個位置以保持整體順序,
第一個數組中的最大元素(10)需要插入到第二個數組的第五個位置。
因此,兩個數組中的 [1, 2, 3] 和 [12, 14, 17] 已經位于它們的最終位置,無需移動。我們實際上需要合并的部分是 [6, 10] 和 [4, 5, 7, 9]。
在這種情況下,我們只需要創建一個大小為 2 的臨時數組,將[6, 10]復制到其中,然后在原數組中將它們與[4, 5, 7, 9]合并。
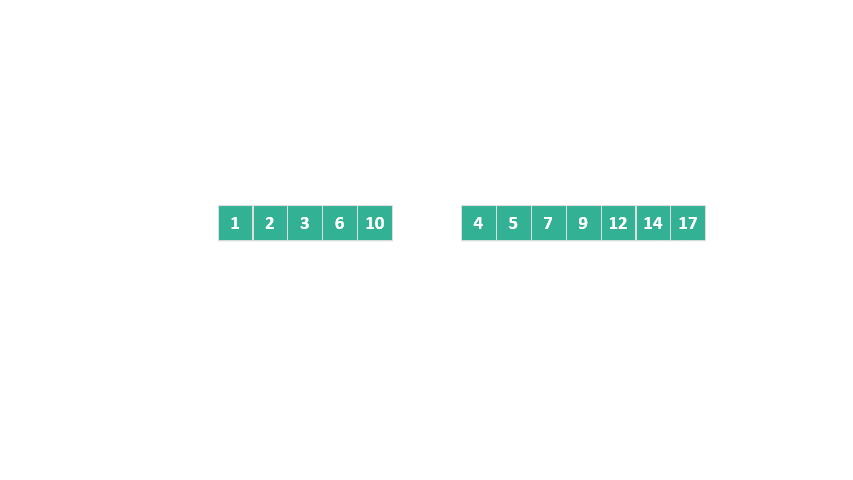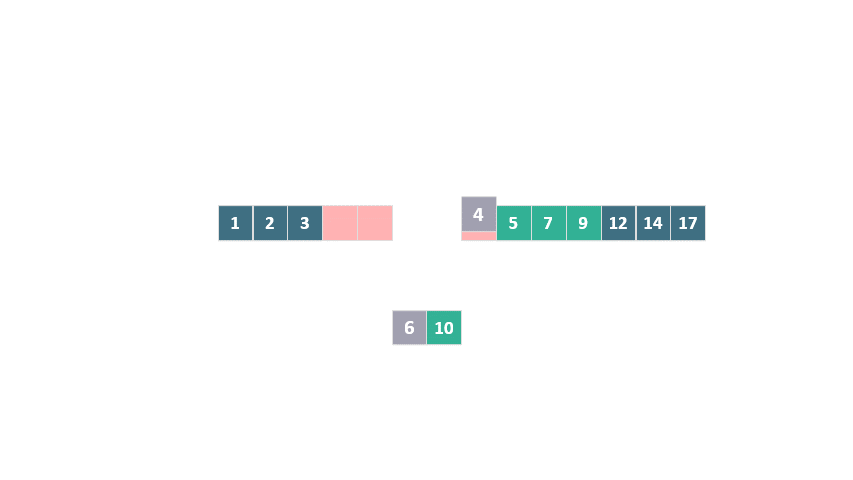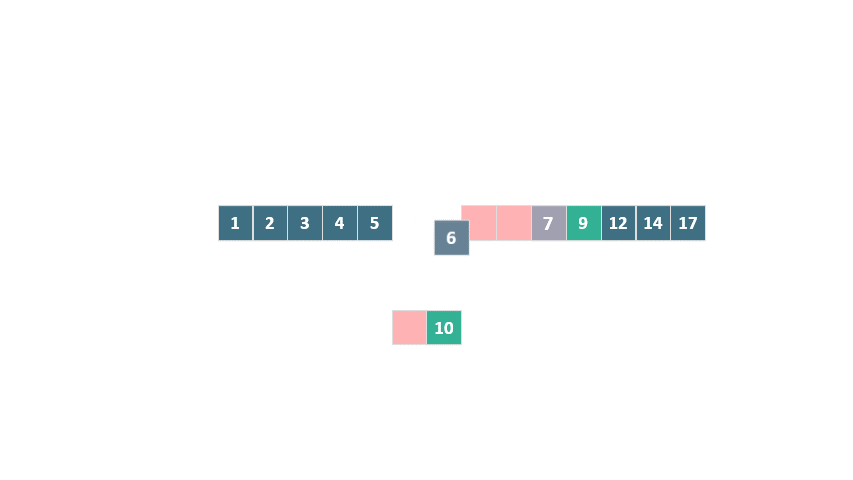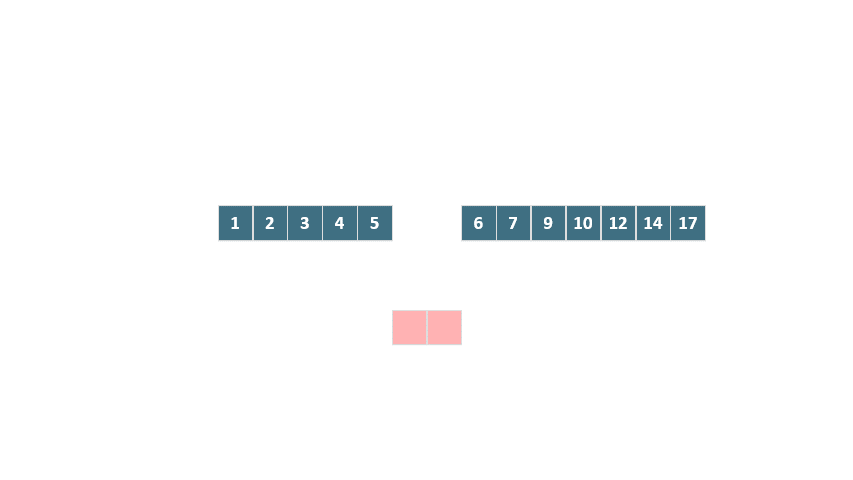
動圖 歸并排序 優化合并過程
這個例子展示了從前往后的合并過程。同樣,還有從后往前合并的情況:
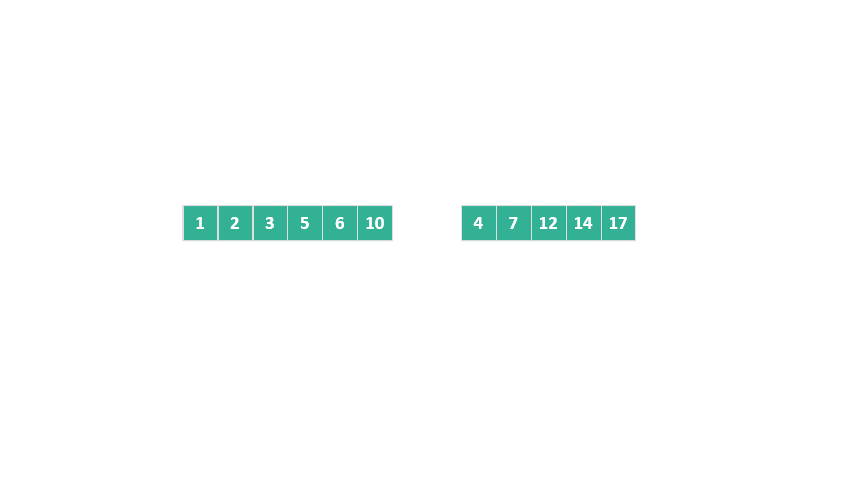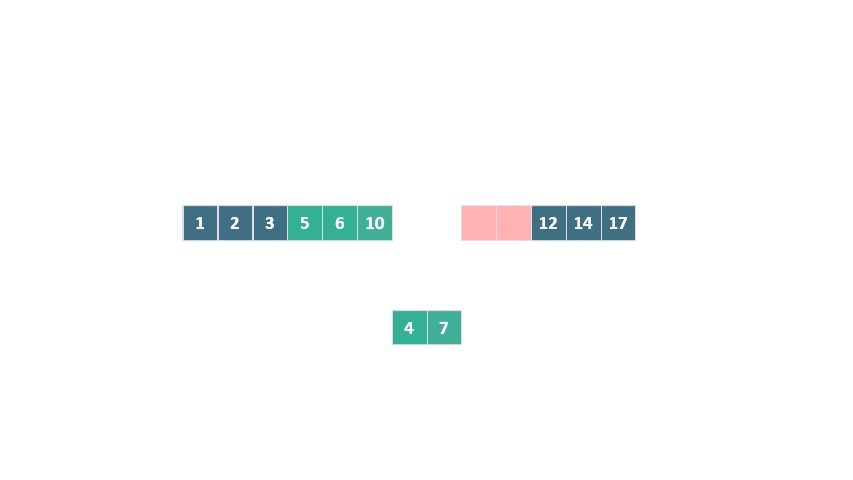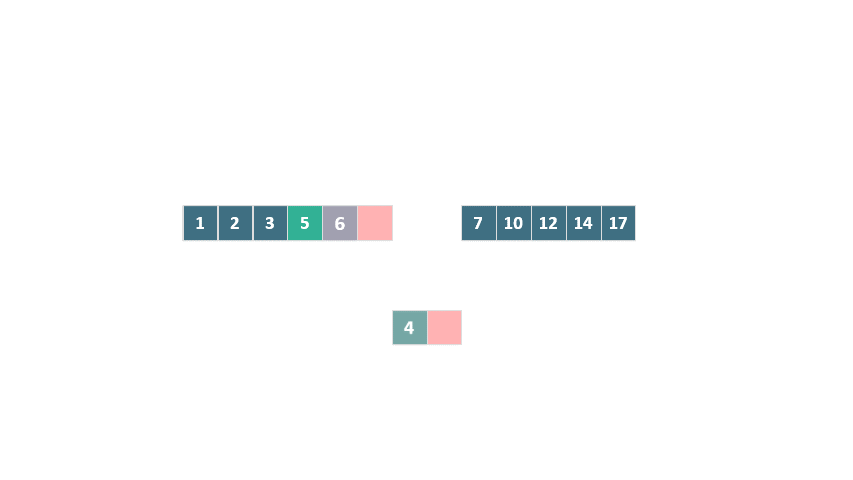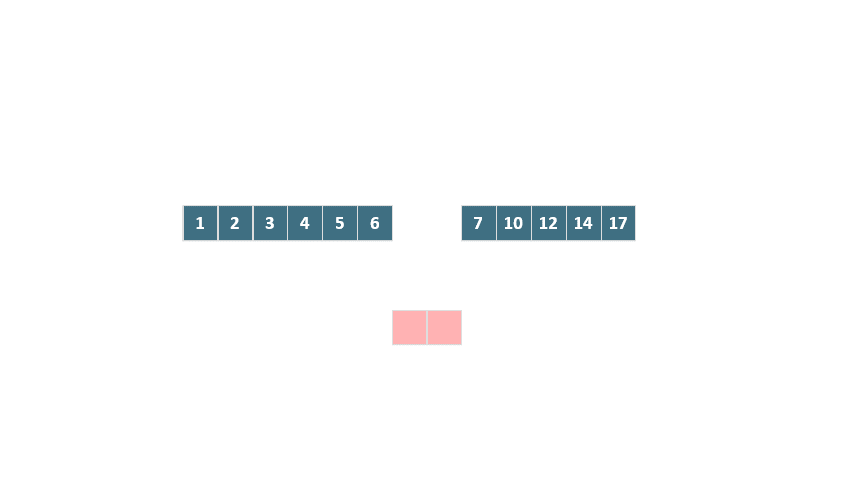
動態圖 歸并排序 從后往前合并
與傳統歸并排序相比,TimSort 在這里采用的優化策略顯著減少了元素移動的次數,縮短了運行時間,并大幅降低了臨時空間的需求。
合并過程中的 galloping mode
在歸并排序過程中,通常的做法是逐個比較兩個數組中的元素,并將較小的元素依次放置到合適的位置。
然而,在某些情況下,這種方法可能涉及大量冗余的比較操作,尤其是當一個數組中的元素連續地勝出另一個數組時。
想象一下,如果我們有兩個極端不平衡的數組:
A = [1, 2, 3, …, 9999, 10000]
B = [20000, 20001, …, 29999, 30000]
在這種情況下,為了確定 B 中元素的正確插入點,我們需要進行高達 10000 次的比較,這無疑是低效的。
如何解決這個問題呢?
TimSort 的解決方案是引入了所謂的“躍進模式”(galloping mode)。這種模式基于一個假設:如果一個數組中的元素連續勝出另一個數組中的元素,那么這種趨勢可能會持續下去。
TimSort 會統計從一個數組連續選中的元素數量,一旦連續勝出次數達到了稱為 min_gallop 的閾值時,TimSort 就會切換到躍進模式。
在這種模式下,算法將不再逐個比較元素,而是將實施一種指數級搜索(exponential search)。以指數級的步長(2^k)進行跳躍,首先檢查位置 1 的元素,然后是位置 3 (1 + 2^1 ),接著是位置 7 (3 + 2^2),以此類推。
當首次找到大于或等于比較元素的位置時,我們就將搜索范圍縮小到上一步的位置(2^(k-1) + 1)和當前步的位置(2^k + 1)之間的區間。
在這個區間內進行更二分搜索,以快速定位正確的插入位置。
據開發者的基準測試,只有當一個數組的首元素并不處于另一數組的前 7 位置時,躍進模式才真正帶來優勢,因此 min_gallop 的閾值為 7。
上面的步驟看起來比較復雜,我們以兩個數組為例:
A = [1, 25, 31, 37]
B = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36]
根據之前合并過程中的空間開銷原則,A 中的元素 1 是固定的,此時將25, 31, 37 移動到臨時空間進行合并排序。
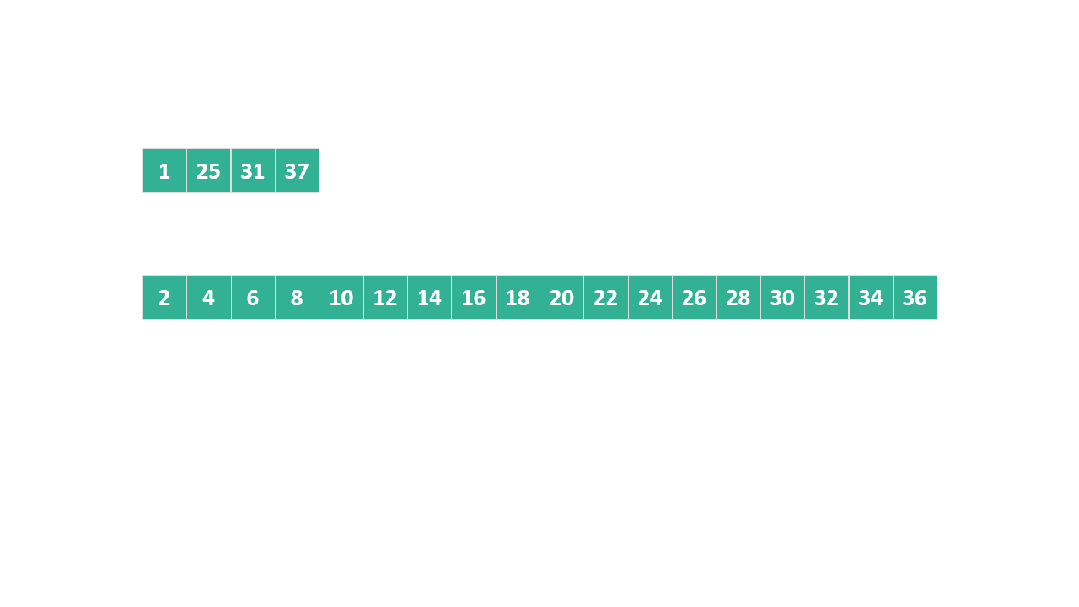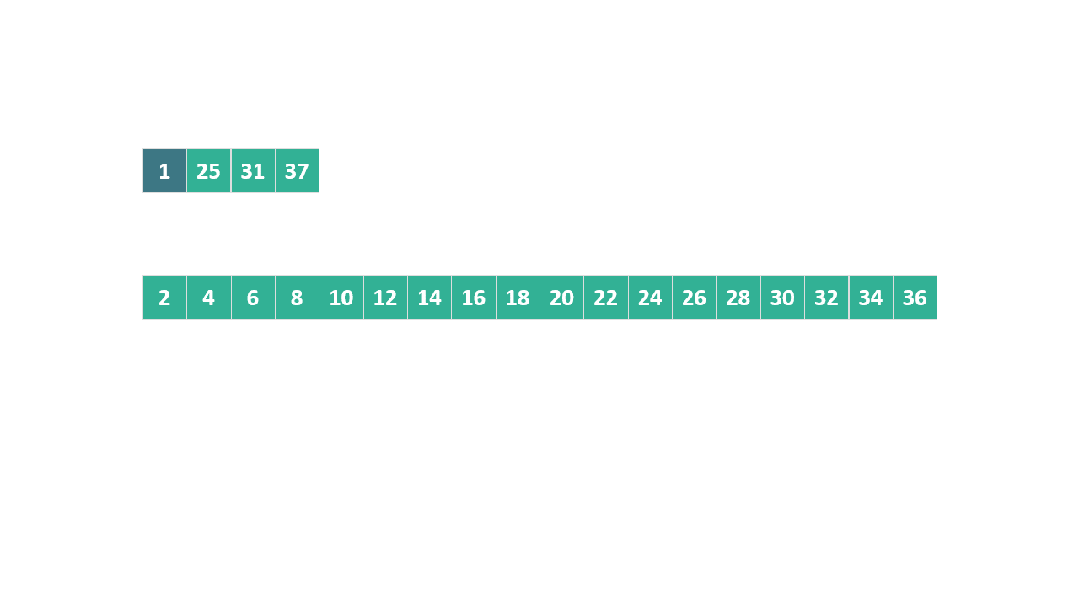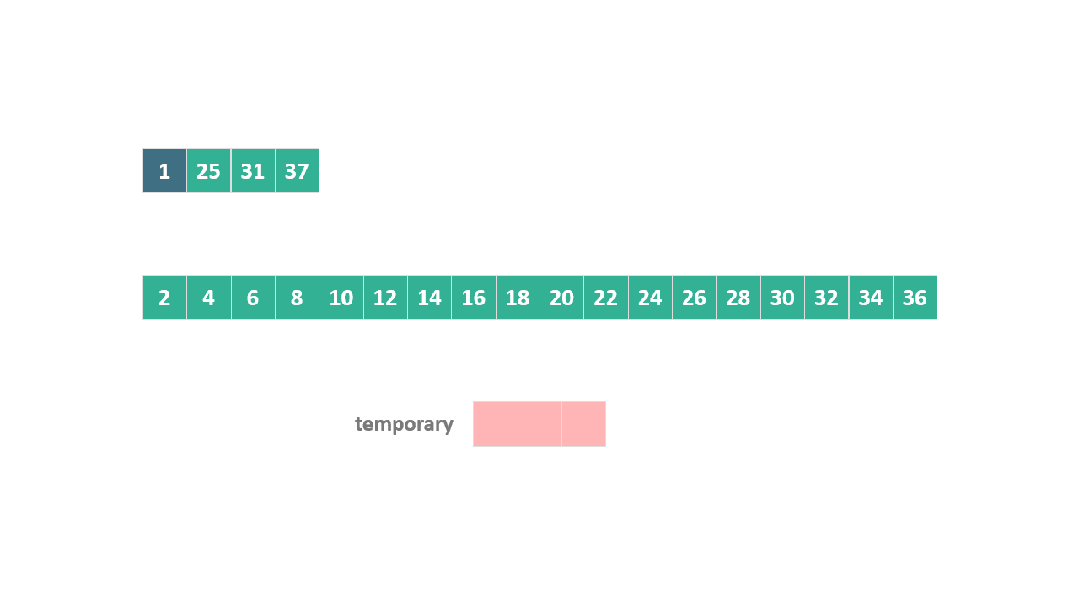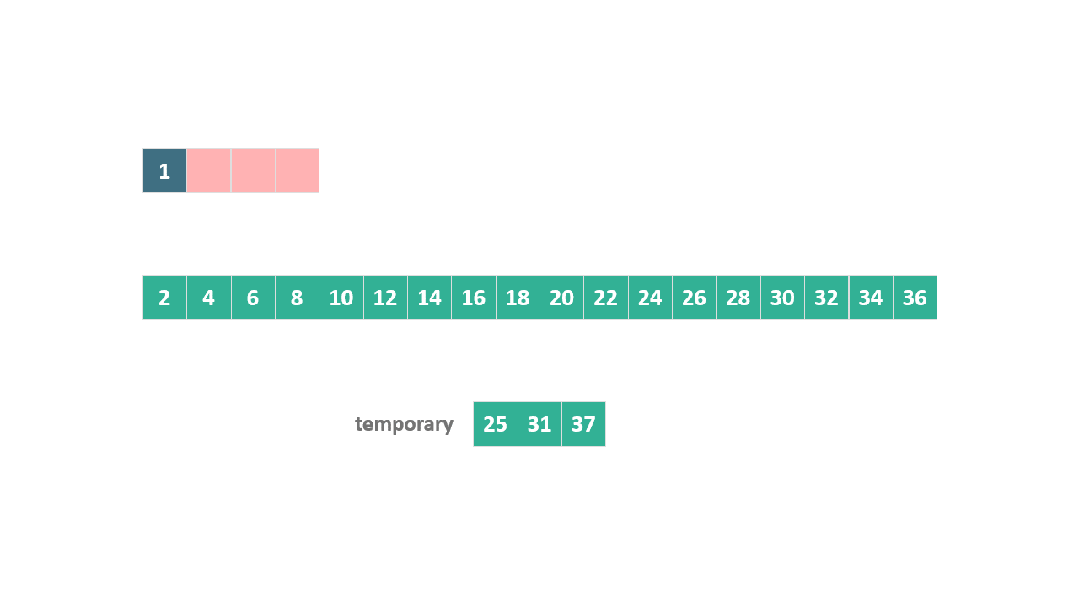
動圖 躍進模式 1
在這種情況下,當 25 在與 B 數組元素比較時連續勝出,觸發了躍進模式。
動圖 躍進模式 2
算法直接跳躍到位置 15 (7 + 2^3),發現 30 大于 25。
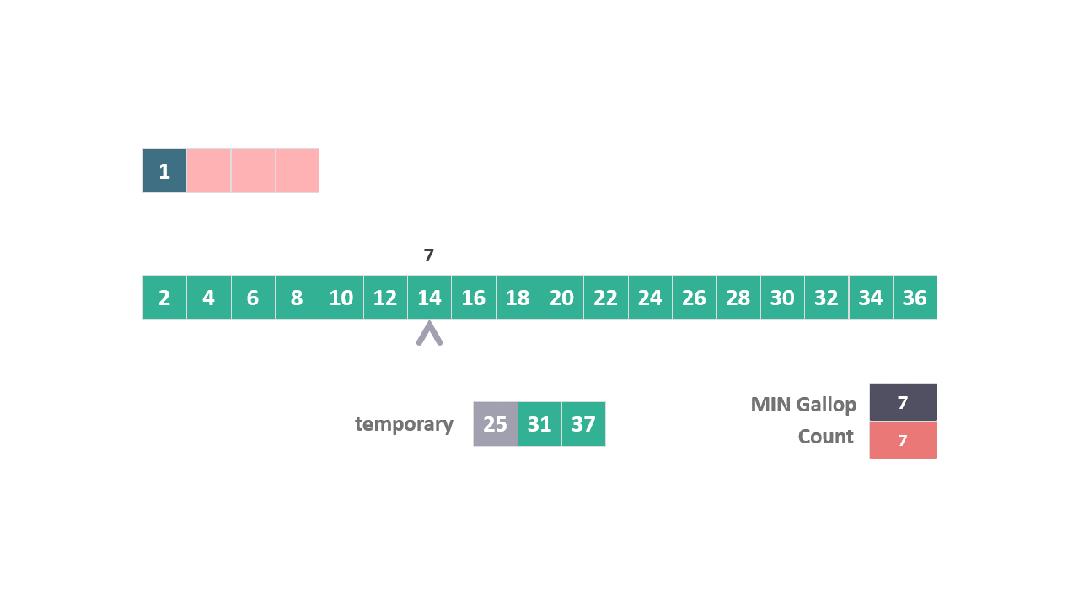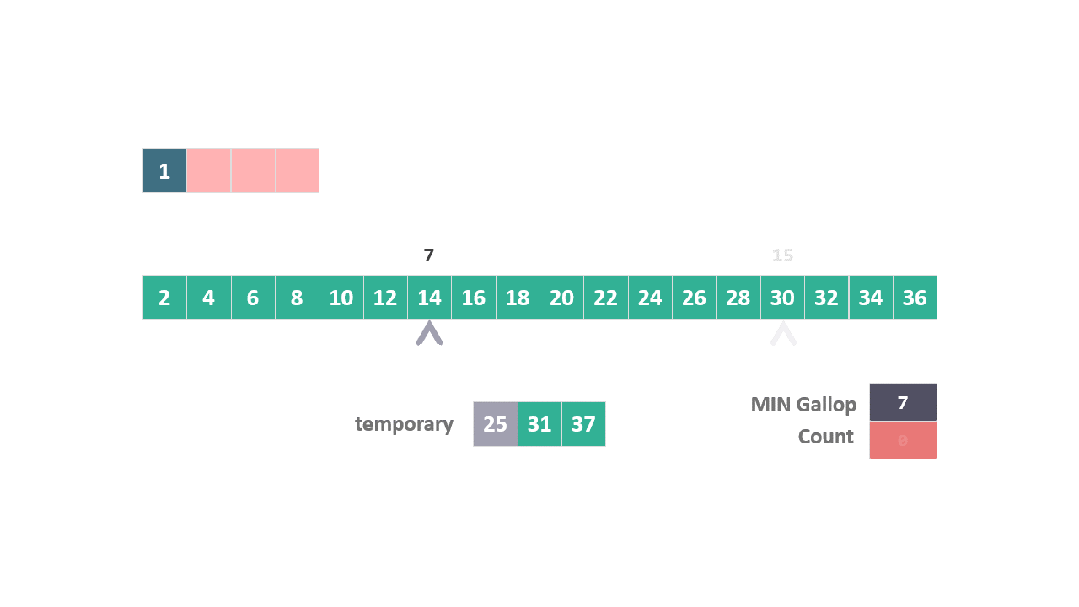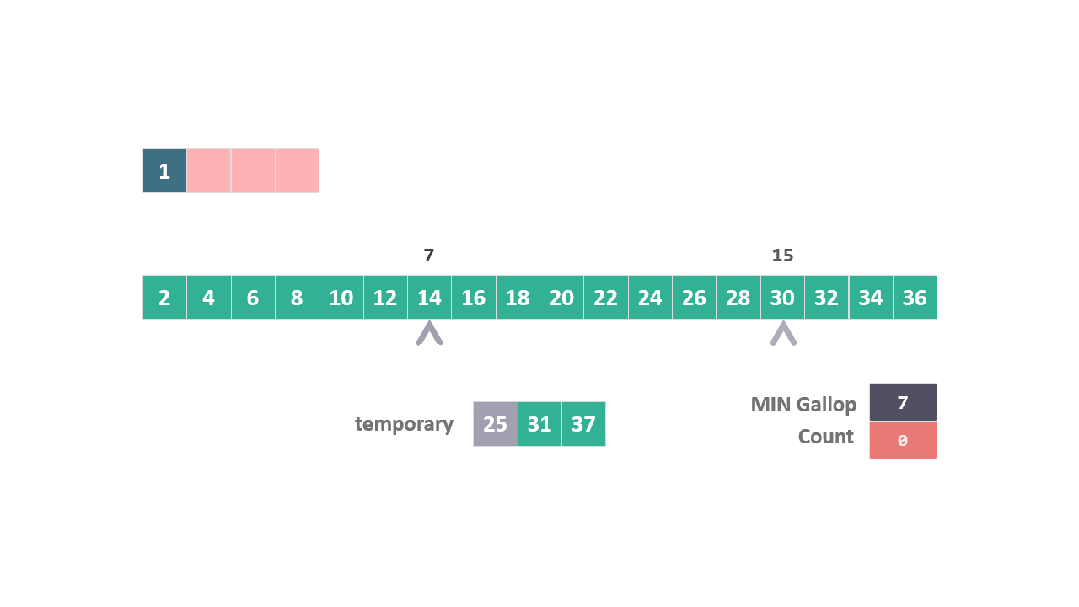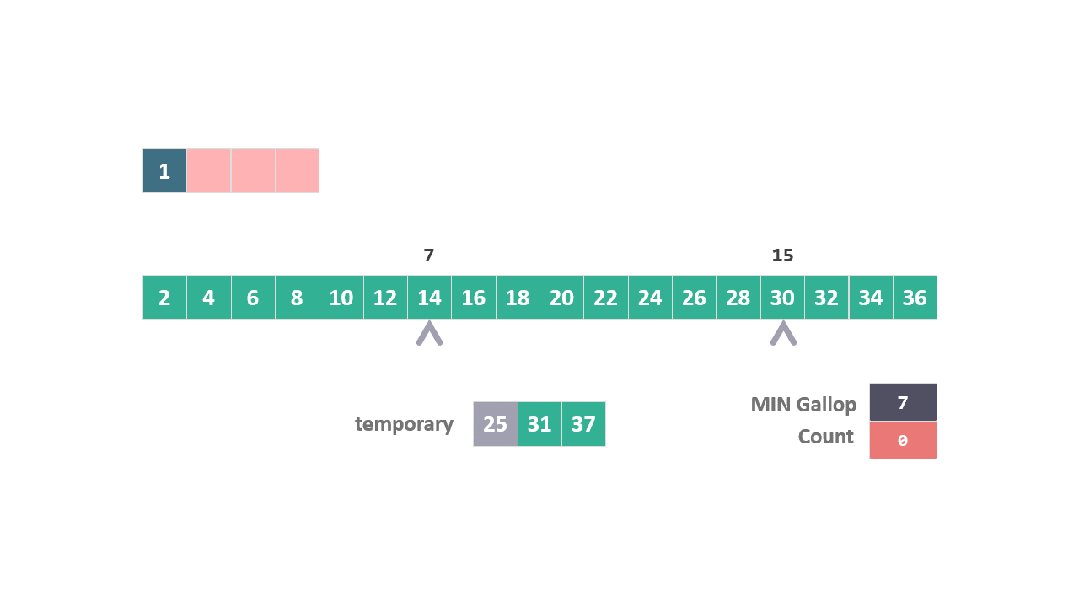
動圖 躍進模式 3
進而在位置 7 和 15 之間執行二分搜索,以找到 25 的插入點。
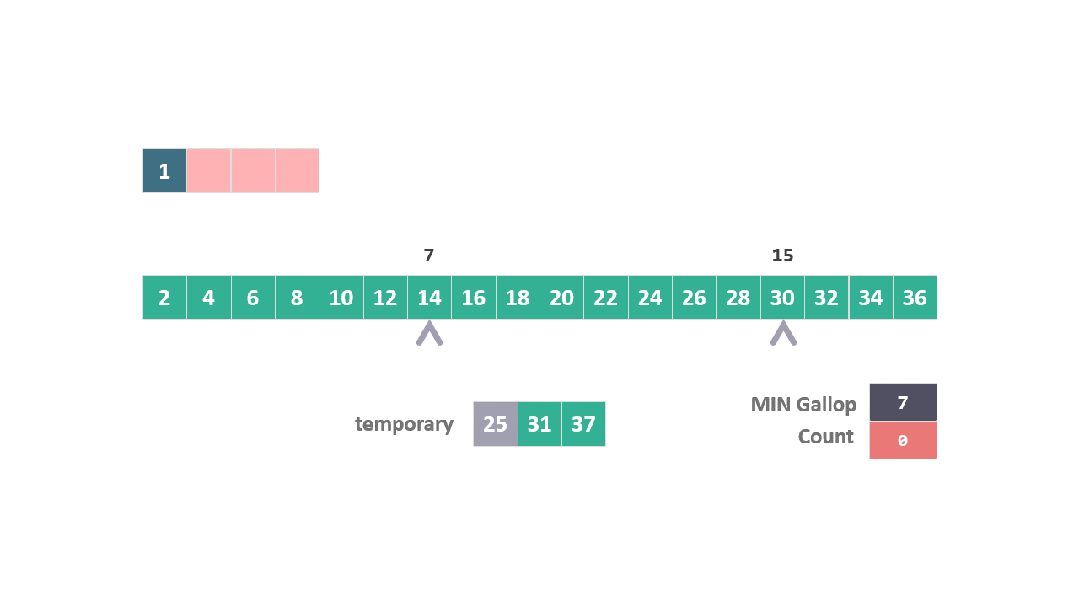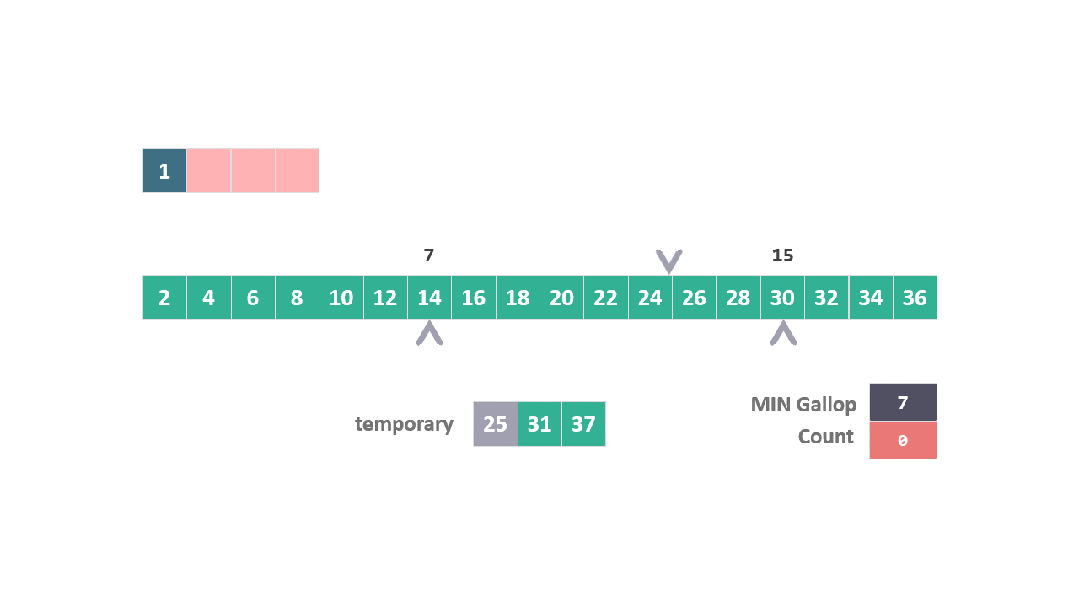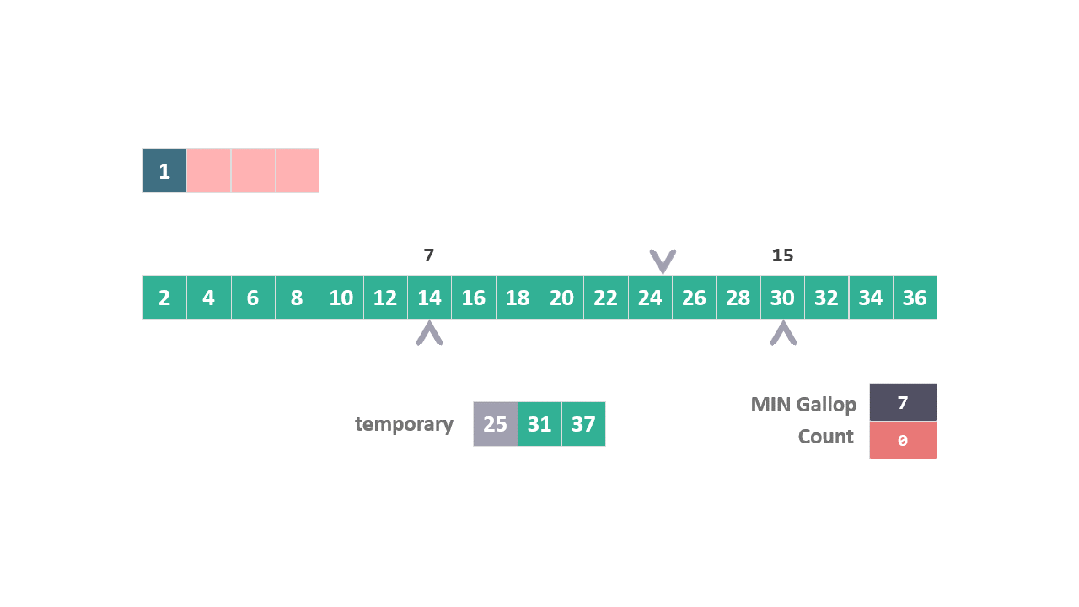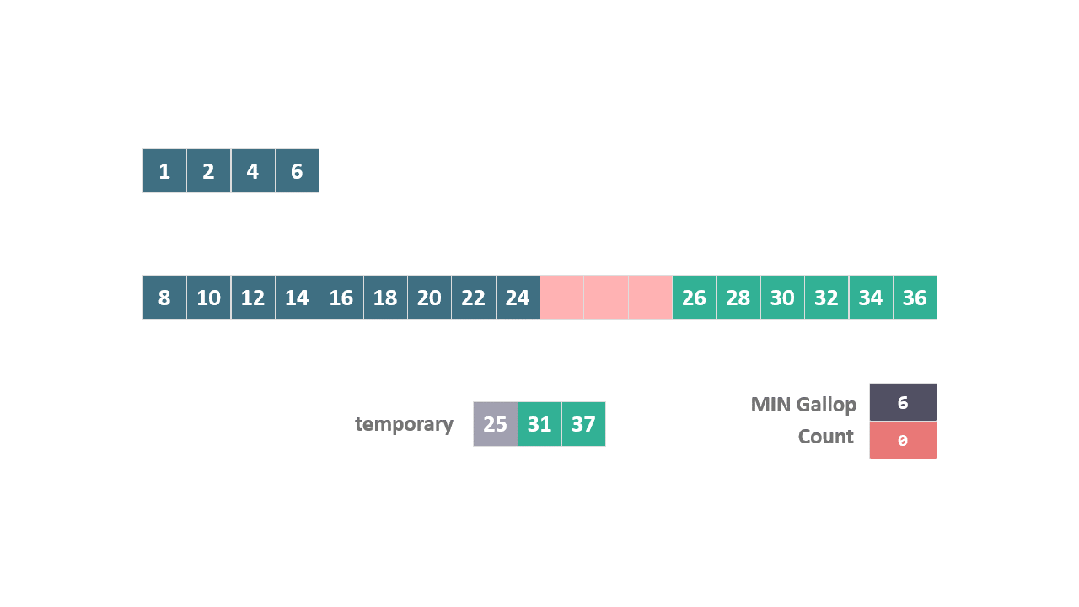
動圖 躍進模式 4
雖然躍進模式在某些情況下能極大提高效率,但它并非總是最優選擇。有時,躍進模式可能導致更多的比較操作,尤其是在數據分布較為均勻時。
為了避免這種情況,TimSort采用了兩種策略:一是當識別到躍進模式的效率不及二分搜索時,會退出躍進模式;二是根據躍進模式的成功與否調整 min_gallop 值。
如果躍進模式成功且連續選擇的元素均來自同一數組,min_gallop 值會減 1,以鼓勵再次使用躍進模式;反之,則加 1,減少再次使用躍進模式的可能性。
結語:TimSort - 數據排序的實用革新
在探索數據排序這個歷史悠久且充滿挑戰的領域中,TimSort 算法不僅是一項技術成就,更是實用性與創新的杰出典范。它的出現,不單單是算法領域的一個新節點,更是對現實世界復雜數據處理需求的有效回應。
TimSort 的真正魅力不僅在于它的高效率,更在于它對實際數據特性的深入理解和利用。這個算法不是靜態的,它通過對數據的觀察,動態調整自身策略,以適應不同的數據模式。
這種設計思路提供了一個重要的啟示:在面對現實世界問題時,理論和實踐的結合往往比單純追求理論完美更為重要。
通過本文的深入分析,我們對 TimSort 的工作原理及其核心概念有了更為直觀的理解。現在,如果再次回顧它的定義,您會發現自己有了更深刻的認識。
參考資料:
[1] https://en.wikipedia.org/wiki/Timsort
[2] https://dev.to/brandonskerritt/timsort-the-fastest-sorting-algorithm-you-ve-never-heard-of-2ake
[3] https://www.infopulse.com/blog/timsort-sorting-algorithm
[4] https://juejin.cn/post/6844904131518267400
[5] https://www.youtube.com/watch?v=_dlzWEJoU7I
[6] https://www.youtube.com/watch?v=1wAOy88WxmY
-
函數
+關注
關注
3文章
4333瀏覽量
62708 -
排序算法
+關注
關注
0文章
53瀏覽量
10080
原文標題:這么多年排序白學了,原來每次排序都在使用世界上最快的排序算法 TimSort
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
HAL庫在Arduino平臺上的使用
常用SQL函數及其用法
怎么在TMDSEVM6678: 6678自帶的FFT接口和CUDA提供CUFFT函數庫選擇?
為什么在水文計算中廣泛采用配線法
利用vMeasure eMobilityAnalyzer函數庫分析電機性能
使用STM32FEBKC6T6開發FOC,如何使用函數庫?
CMSIS的DSP數字信號處理函數庫應用

FPGA實現雙調排序算法的探索與實踐





 TimSort:一個在標準函數庫中廣泛使用的排序算法
TimSort:一個在標準函數庫中廣泛使用的排序算法














評論