不管你怎樣看待數(shù)據(jù)科學(xué)家的研究工作,都不能輕易忽略對(duì)數(shù)據(jù)進(jìn)行分析、組織和梳理的重要性。Glassdoor 網(wǎng)站收集了大量的雇主和員工的反饋數(shù)據(jù),發(fā)現(xiàn)數(shù)據(jù)科學(xué)家位列 "美國(guó)最好的 25 個(gè)職位"榜首。盡管摘得這一桂冠,但需要數(shù)據(jù)科學(xué)家們研究的工作內(nèi)容還在不斷新增。隨著機(jī)器學(xué)習(xí)等技術(shù)越來越普遍的應(yīng)用,深度學(xué)習(xí)等熱門領(lǐng)域受到研究人員和工程師以及企業(yè)的關(guān)注日漸增加,數(shù)據(jù)科學(xué)家必將繼續(xù)站在技術(shù)創(chuàng)新的浪潮之巔,引領(lǐng)著時(shí)代的技術(shù)變革。
因此他們需要系統(tǒng)地研究統(tǒng)計(jì)機(jī)器學(xué)習(xí),該學(xué)科脫胎于統(tǒng)計(jì)學(xué)和泛函分析,并結(jié)合了信息論、最優(yōu)化理論和線性代數(shù)等多門學(xué)科。盡管強(qiáng)大的編程能力對(duì)數(shù)據(jù)科學(xué)家而言十分重要,但數(shù)據(jù)科學(xué)家也不完全就是軟件工程師。事實(shí)上熟練掌握Python對(duì)于他們就已足夠,真正重要的是同時(shí)具備編程、統(tǒng)計(jì)和批判思維的能力。
正如Josh Wills所言:“數(shù)據(jù)科學(xué)家比程序員擅長(zhǎng)統(tǒng)計(jì)學(xué),比統(tǒng)計(jì)學(xué)家擅長(zhǎng)編程。” 很多軟件工程師想轉(zhuǎn)型數(shù)據(jù)科學(xué)家,但他們盲目地使用 TensorFlow 或 Apache Spark 等機(jī)器學(xué)習(xí)框架來處理數(shù)據(jù),卻忽略了背后的統(tǒng)計(jì)學(xué)理論知識(shí)。也就是統(tǒng)計(jì)學(xué)習(xí)理論,機(jī)器學(xué)習(xí)的理論框架,這些都源自統(tǒng)計(jì)學(xué)和泛函分析。
那么為什么要學(xué)習(xí)統(tǒng)計(jì)學(xué)習(xí)?我們只有深刻理解了不同技術(shù)背后的想法,才能學(xué)以致用。也只有先易后難,才能游刃有余、融會(huì)貫通。同時(shí),準(zhǔn)確評(píng)估一種方法的性能也非常重要,不僅能知道工作效果的好壞,也能得知方法的適用范圍。此外,統(tǒng)計(jì)學(xué)習(xí)也是一個(gè)令人振奮的研究領(lǐng)域,在科學(xué)、工業(yè)和金融領(lǐng)域都有重要的應(yīng)用。最后,統(tǒng)計(jì)學(xué)習(xí)是培養(yǎng)現(xiàn)代數(shù)據(jù)科學(xué)家的基礎(chǔ)要素。統(tǒng)計(jì)學(xué)習(xí)問題應(yīng)用的例子如下:
確定前列腺癌的風(fēng)險(xiǎn)因素
根據(jù)對(duì)數(shù)周期圖對(duì)錄音進(jìn)行分類
根據(jù)人口統(tǒng)計(jì)學(xué)、飲食和臨床測(cè)量預(yù)測(cè)是否會(huì)患有心臟病
定制垃圾郵件檢測(cè)系統(tǒng)
識(shí)別手寫郵政編碼
對(duì)組織樣本進(jìn)行癌癥分類
建立人口調(diào)查數(shù)據(jù)中的薪資與人口統(tǒng)計(jì)變量的關(guān)系
在介紹常用的10種統(tǒng)計(jì)技術(shù)之前,我們需要先區(qū)分一下機(jī)器學(xué)習(xí)和統(tǒng)計(jì)學(xué)習(xí),主要有以下幾點(diǎn)區(qū)別:
機(jī)器學(xué)習(xí)是人工智能的一個(gè)分支
統(tǒng)計(jì)學(xué)習(xí)是統(tǒng)計(jì)領(lǐng)域的一個(gè)分支
機(jī)器學(xué)習(xí)更側(cè)重于大規(guī)模應(yīng)用和預(yù)測(cè)的精準(zhǔn)性
統(tǒng)計(jì)學(xué)習(xí)強(qiáng)調(diào)模型及其解釋性、精度和不確定性
但區(qū)別也在變得越來越模糊,兩者很多時(shí)候交織在一起
不得不說,市場(chǎng)營(yíng)銷把機(jī)器學(xué)習(xí)炒得很熱
線性回歸
在統(tǒng)計(jì)學(xué)中,線性回歸是一種通過擬合因變量和自變量之間的最佳線性關(guān)系來預(yù)測(cè)目標(biāo)變量的方法。最佳擬合即表示由當(dāng)前的線性表達(dá)式得到的預(yù)測(cè)輸出與實(shí)際觀測(cè)值的誤差和最小。
線性回歸主要分為簡(jiǎn)單線性回歸和多元線性回歸。簡(jiǎn)單線性回歸使用一個(gè)自變量來擬合最佳線性關(guān)系預(yù)測(cè)因變量;而多元線性回歸使用多個(gè)自變量來擬合最佳線性關(guān)系預(yù)測(cè)因變量。
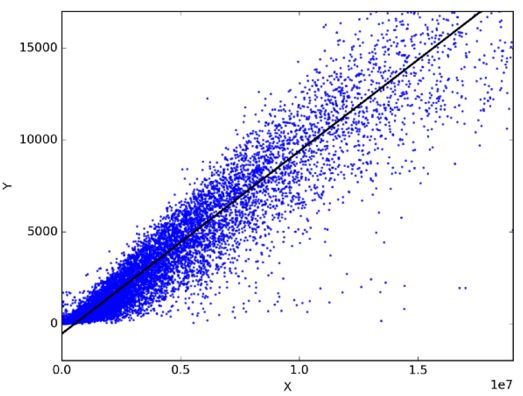
那么線性回歸可以用在哪些實(shí)際問題上呢?實(shí)際上任意選擇日常生活中相關(guān)的兩件事,你便能通過線性回歸模型得到他們之間的線性關(guān)系。比如你有了過去三年的月消費(fèi)、月收入和月旅行次數(shù)的數(shù)據(jù),那你可以預(yù)測(cè)下一年月支出,還可以知道是月收入還是月旅行次數(shù)對(duì)月消費(fèi)更影響,甚至還能用方程式表達(dá)月收入、月旅行次數(shù)、月消費(fèi)三者之間的關(guān)系呢。
分類
分類是屬于一種數(shù)據(jù)挖掘技術(shù),將數(shù)據(jù)集分成多個(gè)類別可以幫助更準(zhǔn)確的預(yù)測(cè)和分析。分類是一種高效分析大型數(shù)據(jù)集的方法,典型的代表有邏輯回歸(Logistic Regression) 分析和判別分析(Discriminant Analysis)。
邏輯回歸分析適合用于因變量為二元類別時(shí)的回歸分析。 和所有回歸分析一樣,邏輯回歸也屬于預(yù)測(cè)分析。 Logistic回歸用于描述數(shù)據(jù),并解釋二元因變量與一個(gè)或多個(gè)名義、序數(shù)、區(qū)間或比率級(jí)別等描述性的自變量之間的關(guān)系。 適合邏輯回歸的問題類型有:
體重每超出標(biāo)準(zhǔn)體重一磅或每天每抽一包煙對(duì)得肺癌概率是否有影響(是或否)。
卡路里攝入、脂肪攝入和年齡對(duì)心臟病是否有影響(是或否)。
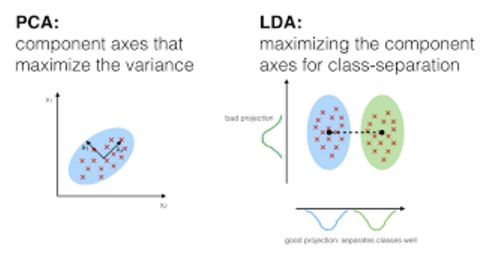
在判別分析中,兩個(gè)或多個(gè)已知的集合、簇或群體都可以作為分類的先驗(yàn)知識(shí),使用時(shí)根據(jù)被測(cè)特征就可把新的觀測(cè)值劃分到相應(yīng)類別。判別分析會(huì)對(duì)每個(gè)類中的預(yù)測(cè)因素 X 分別進(jìn)行建模,然后根據(jù)貝葉斯定理便能將其轉(zhuǎn)換成只需根據(jù) X 值就可獲得對(duì)應(yīng)類別的概率估計(jì)。此類模型既可以是線性判別分析,也可以是二次判別分析。
Linear Discriminant Analysis線性判別分析,通過自變量的線性組合對(duì)每個(gè)觀測(cè)值計(jì)算“判別分?jǐn)?shù)”,并對(duì)其所處的響應(yīng)變量Y類別進(jìn)行分類。它假設(shè)每個(gè)類別內(nèi)的觀測(cè)值都服從多變量高斯分布,且每個(gè)類別的方差一樣。
Quadratic Discriminant Analysis二次判別分析,提供了另一種方法。與LDA一樣,QDA也假設(shè)來自Y的每類觀察值都服從高斯分布。但與LDA不同的是,QDA假定每個(gè)類別都有其自己的協(xié)方差矩陣,也就是說每個(gè)類別的方差不一樣。
重采樣方法
重采樣方法就是從原始數(shù)據(jù)樣本中重復(fù)提取樣本,屬于統(tǒng)計(jì)推斷的非參數(shù)方法。重采樣不使用通用分布表來逼近地計(jì)算概率 p 的值,而是基于實(shí)際數(shù)據(jù)生成一個(gè)獨(dú)特的采樣分布。這種采用分布通過經(jīng)驗(yàn)性方法生成,而不是分析方法,它能夠基于數(shù)據(jù)所有可能結(jié)果的無偏樣本獲取無偏估計(jì)。為了很好的理解重采樣的概念,我們需要先了解Bootstrapping和交叉驗(yàn)證(Cross-Validation):
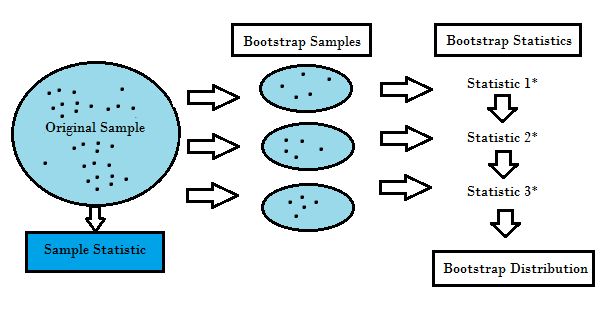
Bootstrapping是有助于在許多情況下驗(yàn)證預(yù)測(cè)模型的性能和集成方法,估計(jì)模型的偏差和方差。 它通過對(duì)原始數(shù)據(jù)進(jìn)行有放回的采樣,并將“未被選擇”的數(shù)據(jù)點(diǎn)作為測(cè)試用例。 我們可以多做幾次這樣的操作,然后用平均值來作為我們對(duì)模型性能的估計(jì)。
Cross validation交叉驗(yàn)證通過將訓(xùn)練數(shù)據(jù)分成k個(gè)部分來驗(yàn)證模型性能,使用k-1部分作為訓(xùn)練集,余下的部分作為測(cè)試集。 重復(fù)不同的k次后,將k個(gè)分?jǐn)?shù)的平均值作為模型的性能估計(jì)。
通常對(duì)于線性模型而言,普通的最小二乘法是擬合數(shù)據(jù)時(shí)的主要標(biāo)準(zhǔn)。 接下來的3種方法可以為線性模型擬合提供更好的預(yù)測(cè)精度和模型可解釋性。
子集選擇
子集選擇的主要目的是挑選出與問題最相關(guān)的 p 個(gè)預(yù)測(cè)因子,然后使用該子集特征和最小二乘法擬合模型。
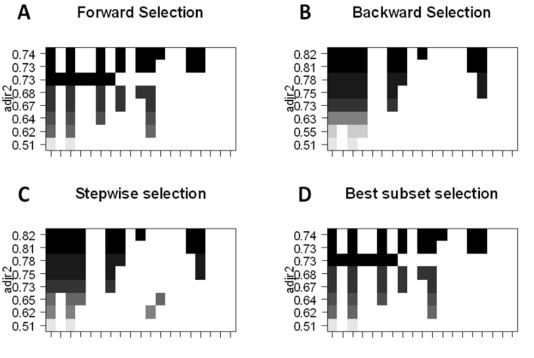
最佳子集的選擇,我們可以為 p 個(gè)預(yù)測(cè)因子的每個(gè)組合分別擬合普通最小二乘回歸,然后再觀察各個(gè)模型的擬合結(jié)果。算法分為兩個(gè)階段:(1)擬合包含 k 個(gè)預(yù)測(cè)因子的所有模型,其中 k 表示模型的最大長(zhǎng)度;(2)使用交叉驗(yàn)證預(yù)測(cè)損失選擇單個(gè)模型。要記住,不能單純使用訓(xùn)練誤差評(píng)估模型的擬合情況,驗(yàn)證集或測(cè)試集的誤差也是十分重要的,因?yàn)?RSS 和 R^2 會(huì)隨變量的增加而單調(diào)遞增。最好的方法就是通過選擇測(cè)試集中最高的 R^2 和最低的 RSS 來交叉驗(yàn)證,從而選擇模型。
前向逐步選擇,可以選出 p 個(gè)預(yù)測(cè)因子的較小子集。算法先從不包含預(yù)測(cè)因子的模型開始,然后逐步地添加預(yù)測(cè)因子到模型中,直到所有預(yù)測(cè)因子都包含在模型中。添加預(yù)測(cè)因子的順序是根據(jù)不同變量對(duì)模型擬合性能提升的程度來確定的,不斷添加新的預(yù)測(cè)因子,直到交叉驗(yàn)證誤差沒有大的改變。
后向逐步選擇,與前向逐步選擇相反,首先模型包含所有 p個(gè) 預(yù)測(cè)因子,然后迭代地移除用處最小的預(yù)測(cè)因子。
混合法,主體遵循前向逐步方法,但在添加每個(gè)新變量之后,該方法可能還會(huì)移除對(duì)模型擬合無用的變量。
特征縮減技術(shù)
特征縮減技術(shù)使用了所有 p 個(gè)預(yù)測(cè)因子進(jìn)行建模,然而,表示預(yù)測(cè)因子重要性的系數(shù)將隨最小二乘誤差向零收縮,這種收縮也稱之為正則化,它旨在減少方差以防止模型的過擬合。常用的縮減系數(shù)方法有l(wèi)asso(L1正則化),嶺回歸(L2正則化)。
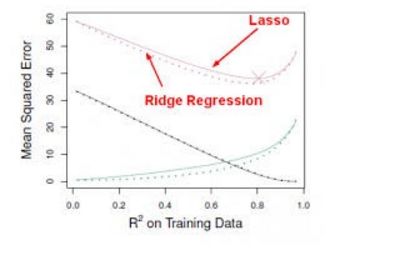
Ridge regression嶺回歸,跟最小二乘法很像都是尋求減少 RSS 的系數(shù)估計(jì),只不過它是通過對(duì)損失函數(shù)(即優(yōu)化目標(biāo))加入懲罰項(xiàng),使得訓(xùn)練求解參數(shù)過程中會(huì)考慮到系數(shù)的大小。我們不需要數(shù)學(xué)分析就能看出 Ridge 回歸很擅長(zhǎng)于將特征收縮到最小的子空間中。如主成分分析PCA,通過Ridge 回歸可以將數(shù)據(jù)投影到低維空間,并在系數(shù)空間內(nèi)收縮較低方差的成分而保留有較高方差的成分。
但Ridge 回歸有一個(gè)缺點(diǎn),最終的模型需要包含所有 p 個(gè)預(yù)測(cè)因子,這源于盡管懲罰項(xiàng)將會(huì)令許多預(yù)測(cè)因子的系數(shù)逼近零,但又一定不等于零。雖然這對(duì)預(yù)測(cè)準(zhǔn)確度并沒有什么影響,卻令模型的結(jié)果更難以解釋。Lasso 方法就很好的克服了這一缺點(diǎn),因?yàn)樗茉?s 足夠小的時(shí)候迫使一些預(yù)測(cè)因子的系數(shù)歸零。當(dāng) s = 1 時(shí),就像正常的OLS 回歸,而當(dāng) s 逼近 0 時(shí),系數(shù)將收縮到零。因此 Lasso 回歸同樣是執(zhí)行變量選擇的好方法。
降維(維數(shù)減約)
降維是將將p + 1個(gè)系數(shù)估計(jì)問題簡(jiǎn)化為為M + 1系數(shù)估計(jì)問題,其中M
Principal Components Regression主成分回歸,是從大量的變量中尋找低維特征集的方法。數(shù)據(jù)中的第一主成分(first principal component)是指觀測(cè)數(shù)據(jù)沿著這個(gè)變量方向的變化最大,也就是說若用 p 個(gè)不同的主成分分別擬合數(shù)據(jù),那第一主成分必然是最接近數(shù)據(jù)分布的那條線。第二主成分是和第一主成分不相關(guān)的變量的線性組合,且在該約束下有最大的方差。主要思想是主成分能在各個(gè)互相垂直的方向使用數(shù)據(jù)的線性組合得到最大的方差。基于這種方法,我們還能結(jié)合相關(guān)變量的效應(yīng)從數(shù)據(jù)中獲取更多的信息,畢竟在常規(guī)的最小二乘法中需要舍棄其中一個(gè)相關(guān)變量。
由于PCR 方法需要得到 X 的最優(yōu)線性組合。由于 X 對(duì)應(yīng)的輸出 Y 對(duì)主成分方向的計(jì)算沒有影響,也就是說這些組合(方向)是通過無監(jiān)督方法獲得的,那么就無法保證這些方向是預(yù)測(cè)器的最優(yōu)表征,也無法保證能獲得最優(yōu)預(yù)測(cè)輸出。偏最小二乘法(PLS)作為 PCR 的代替方法,屬于有監(jiān)督方法。和 PCR 類似,PLS 也是一種降維方法,它首先提取一個(gè)新的較小的特征集合(原始特征的線性組合),然后通過最小二乘法將原來的模型擬合為一個(gè)新的具有 M 個(gè)特征的線性模型,通過對(duì)模型預(yù)測(cè)誤差來評(píng)價(jià)特征集合是否是Y的最優(yōu)線性組合。
非線性模型
在統(tǒng)計(jì)學(xué)中,非線性回歸屬于回歸分析的一種形式,通過模型參數(shù)的非線性組合來(依賴于一個(gè)或多個(gè)獨(dú)立變量)對(duì)觀測(cè)數(shù)據(jù)建模,并使用逐次逼近法來擬合數(shù)據(jù)。以下是幾種處理非線性模型的重要技術(shù):
階梯函數(shù)(step function),變量為實(shí)數(shù),可以寫成區(qū)間的效用函數(shù)的有限線性組合的形式。通俗的講,階梯函數(shù)就是一種只有有限部分的分段常數(shù)函數(shù)。
分段函數(shù)(piecewise function)通過多個(gè)子函數(shù)定義,且每一個(gè)子函數(shù)被定義在確定的區(qū)間上。分段實(shí)際上是函數(shù)的表示方式,而不是函數(shù)自身特性,但通過額外的限定條件,它也可以用于描述函數(shù)本身。例如,一個(gè)分段多項(xiàng)式函數(shù)是一個(gè)在每一個(gè)子定義上為多項(xiàng)式的函數(shù),其中每一個(gè)多項(xiàng)式都可能是不同的。
樣條曲線(spline)是一種用多項(xiàng)式分段定義的特殊函數(shù)。在計(jì)算機(jī)圖形學(xué)中,樣條曲線是一種分段多項(xiàng)式參數(shù)化曲線。由于結(jié)構(gòu)簡(jiǎn)單、評(píng)估簡(jiǎn)易和精度高,以及通過曲線擬合和交互曲線設(shè)計(jì)就能逼近復(fù)雜曲線的能力,使得樣條曲線很常用。
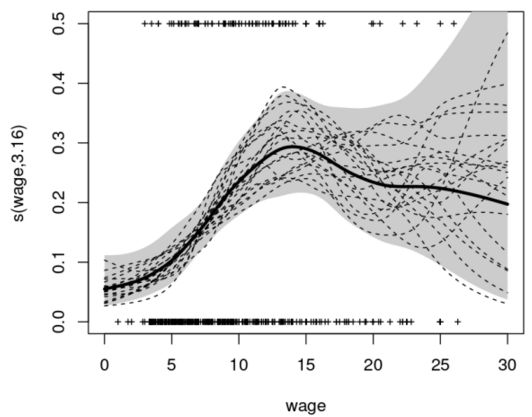
廣義加性模型(generalized additive model)是一種廣義線性模型,其中線性預(yù)測(cè)器線性依賴于某些預(yù)測(cè)器變量的未知平滑函數(shù),其主要作用就是推斷這些平滑函數(shù)。
基于樹的方法
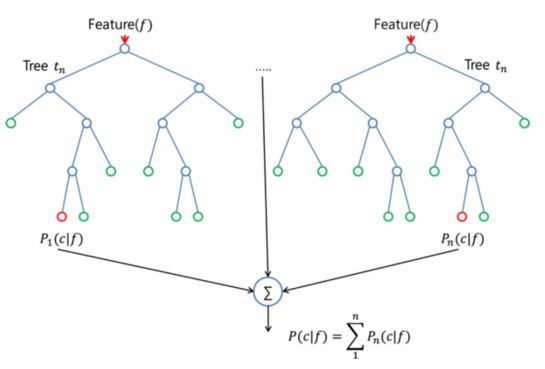
基于樹的方法可以用于回歸和分類問題,它會(huì)將預(yù)測(cè)器空間分層或分割成一些簡(jiǎn)單的區(qū)域。由于預(yù)測(cè)器空間的分裂規(guī)則集合可以總結(jié)為一個(gè)樹,因此也被稱為決策樹方法。以下的方法是幾種不同的樹,它們可以組合起來投票輸出統(tǒng)一的預(yù)測(cè)。
Bagging能通過從原始數(shù)據(jù)中生成額外的訓(xùn)練數(shù)據(jù)(通過組合和重復(fù)生成和原始數(shù)據(jù)大小相同的多段數(shù)據(jù))來減少預(yù)測(cè)的方差,但無法提高模型的預(yù)測(cè)能力。
Boosting是一種計(jì)算輸出的方法,使用多個(gè)不同的模型,然后使用加權(quán)平均的方法對(duì)結(jié)果取平均值。一般結(jié)合各方法的優(yōu)勢(shì)來改變這些方法所占的權(quán)重,此外,針對(duì)更寬泛的輸入數(shù)據(jù)還可以微調(diào)參數(shù)得到更佳的預(yù)測(cè)能力。
隨機(jī)森林算法(random forest algorithm)實(shí)際上和 bagging 算法很相似,同樣是對(duì)訓(xùn)練集提取隨機(jī) bootstrap 樣本。然而,除了 bootstrap 樣本以外,還可以提取特征的隨機(jī)子集來訓(xùn)練單個(gè)樹;在 bagging 中,則需要為每個(gè)樹提供全部的特征。由于特征選擇是隨機(jī)的,相比常規(guī)的bagging 算法,每個(gè)樹之間更加獨(dú)立,從而通常能獲得更好的預(yù)測(cè)性能(得益于更好的方差-偏差權(quán)衡)。由于每個(gè)樹只需要學(xué)習(xí)特征的一個(gè)子集,因此速度也得以提升。
支持向量機(jī)
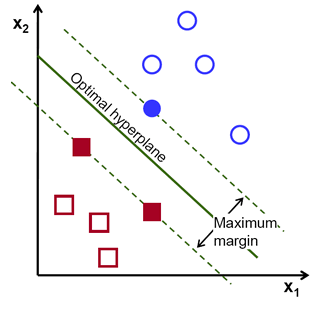
支持向量機(jī)(SVM)是一種常用的有監(jiān)督學(xué)習(xí)分類技術(shù)。通俗地說,它尋找兩類點(diǎn)集的最優(yōu)超平面(hyperplane,在 2D 空間中是線,在 3D 空間中是面,在高維空間中就是超平面。超平面是n 維空間的 n-1 維子空間)。這個(gè)超平面使得兩類點(diǎn)集的間隔最大,本質(zhì)上是約束最優(yōu)化問題,在一定約束下使得間隔最大化,從而實(shí)現(xiàn)數(shù)據(jù)的完美分類。
"支持向量",就是那些支持著超平面的數(shù)據(jù)點(diǎn),也可以說是離超平面最近的數(shù)據(jù)點(diǎn)。在上圖中,藍(lán)色填充圓和兩個(gè)填充方塊就是支持向量。使用過程中,當(dāng)兩類數(shù)據(jù)線性不可分時(shí),數(shù)據(jù)點(diǎn)可以通過核函數(shù)投影到高維空間中,使得數(shù)據(jù)變得線性可分。而多分類問題也可以分解成多個(gè)"一對(duì)一"(one-versus-one)或"一對(duì)剩余"(one-versus-rest)的二分類問題。
無監(jiān)督學(xué)習(xí)
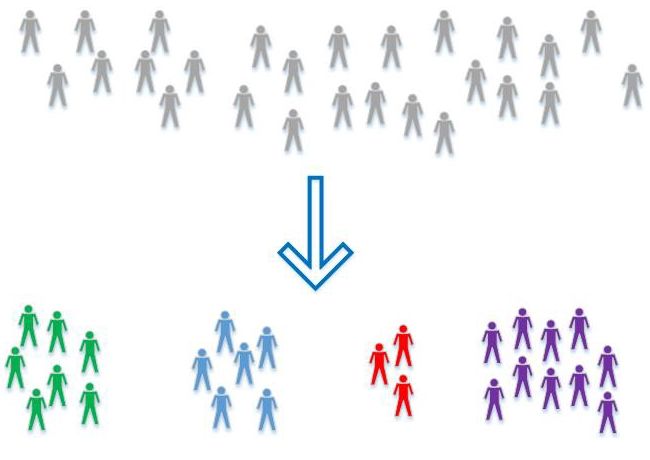
有監(jiān)督學(xué)習(xí)是機(jī)器學(xué)習(xí)中的一大部分,其中數(shù)據(jù)分類已知。當(dāng)數(shù)據(jù)分類是未知時(shí),就需要使用另一種技術(shù)了,就是無監(jiān)督學(xué)習(xí),它們需要自己去發(fā)現(xiàn)數(shù)據(jù)中的模式。聚類(clustring)是一種典型的無監(jiān)督學(xué)習(xí),數(shù)據(jù)會(huì)根據(jù)相關(guān)性被分為多簇。以下是幾種最常用的無監(jiān)督學(xué)習(xí)算法:
Principal Component Analysis主成分分析:通過保留具備最大方差和互相不相關(guān)的特征之間的線性組合,可以生成數(shù)據(jù)集的低維表示。它還有助于理解無監(jiān)督學(xué)習(xí)中的隱變量交互。
k-Means clusteringk 均值聚類:屬于硬聚類算法,根據(jù)數(shù)據(jù)到聚類中心的距離將其分成 k 個(gè)不同的簇。
Hierarchical clustering層次聚類:由于k-means算法始終有K值選擇和初始聚類中心點(diǎn)選擇的問題,而這些問題也會(huì)影響聚類的效果。為了避免這些問題,我們可以選擇另外一種比較實(shí)用的聚類算法,就是層次聚類算法。顧名思義,層次聚類就是一層一層的進(jìn)行聚類,可以自頂向下把大的類別(cluster)分割,叫作分裂法;也可以自下而上對(duì)小的類別進(jìn)行聚合,叫作凝聚法;但是一般用的比較多的是由下向上的凝聚方法。
以上就是一些幫助數(shù)據(jù)科學(xué)家理解數(shù)據(jù)基本的統(tǒng)計(jì)技術(shù),了解這些基本分析技術(shù)將為為項(xiàng)目的開發(fā)和數(shù)據(jù)的理解帶來更多的益處,對(duì)數(shù)據(jù)的抽象和操作會(huì)變得更加容易。希望這篇文章能幫助小伙伴們?cè)诶斫鈹?shù)據(jù)科學(xué)的路上帶來一些新的收獲。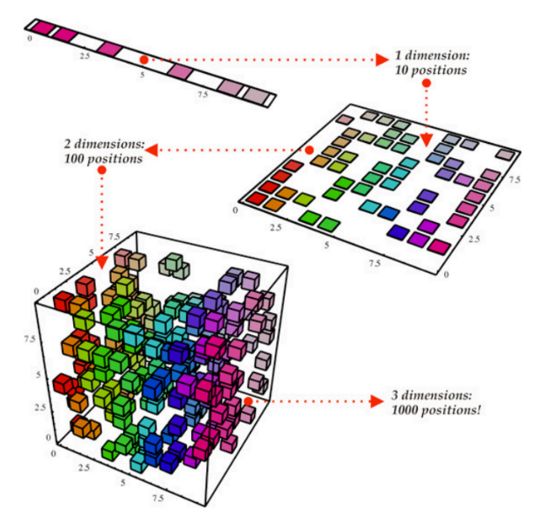
-
線性
+關(guān)注
關(guān)注
0文章
198瀏覽量
25145 -
機(jī)器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8406瀏覽量
132565
原文標(biāo)題:數(shù)據(jù)科學(xué)家必備的10大統(tǒng)計(jì)技術(shù)
文章出處:【微信號(hào):thejiangmen,微信公眾號(hào):將門創(chuàng)投】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦




 了解這些基本分析技術(shù)將為為項(xiàng)目的開發(fā)和數(shù)據(jù)的理解帶來更多的益處
了解這些基本分析技術(shù)將為為項(xiàng)目的開發(fā)和數(shù)據(jù)的理解帶來更多的益處










評(píng)論