本文擬通過(guò)使用 Tensorflow 實(shí)現(xiàn)線性支持向量機(jī)（LinearSVM）的形式來(lái)作為 Tensorflow 的“應(yīng)用式入門(mén)教程”。雖說(shuō)用 mnist 做入門(mén)教程項(xiàng)目幾乎是約定俗成的事了，但總感覺(jué)照搬這么個(gè)東西過(guò)來(lái)當(dāng)專欄有些水……所以還是自己親手寫(xiě)了個(gè) LinearSVM ( σ'ω')σ

在實(shí)現(xiàn)之前，先簡(jiǎn)要介紹一下 LinearSVM 算法（詳細(xì)介紹可以參見(jiàn)這里）：

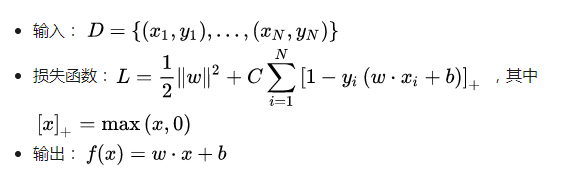
以及介紹一下 Tensorflow 的若干思想：

Tensorflow 的核心在于它能構(gòu)建出一張“運(yùn)算圖（Graph）”，我們需要做的是往這張 Graph 里加入元素

基本的元素有如下三種：常量（constant）、可訓(xùn)練的變量（Variable）和不可訓(xùn)練的變量（Variable(trainable=False)）

由于機(jī)器學(xué)習(xí)算法常常可以轉(zhuǎn)化為最小化損失函數(shù)，Tensorflow 利用這一點(diǎn)、將“最小化損失”這一步進(jìn)行了很好的封裝。具體而言，你只需要在 Graph 里面將損失表達(dá)出來(lái)后再調(diào)用相應(yīng)的函數(shù)、即可完成所有可訓(xùn)練的變量的更新

其中第三點(diǎn)我們會(huì)在實(shí)現(xiàn) LinearSVM 時(shí)進(jìn)行相應(yīng)說(shuō)明，這里則會(huì)把重點(diǎn)放在第二點(diǎn)上。首先來(lái)看一下應(yīng)該如何定義三種基本元素以及相應(yīng)的加、減、乘、除（值得一提的是，在 Tensorflow 里面、我們常常稱處于 Graph 之中的 Tensorflow 變量為“Tensor”，于是 Tensorflow 就可以理解為“Tensor 的流動(dòng)”）（注：Tensor 這玩意兒叫張量，數(shù)學(xué)上是挺有來(lái)頭的東西；然而個(gè)人認(rèn)為如果不是做研究的話就完全可以不管它數(shù)學(xué)內(nèi)涵是啥、把它當(dāng)成高維數(shù)組就好 ( σ'ω')σ）：

import tensorflow as tf

# 定義常量、同時(shí)把數(shù)據(jù)類型定義為能夠進(jìn)行 GPU 計(jì)算的 tf.float32 類型

x = tf.constant(1, dtype=tf.float32)

# 定義可訓(xùn)練的變量

y = tf.Variable(2, dtype=tf.float32)

# 定義不可訓(xùn)練的變量

z = tf.Variable(3, dtype=tf.float32, trainable=False)

x_add_y = x + y

y_sub_z = y – z

x_times_z = x * z

z_div_x = z / x

此外，Tensorflow 基本支持所有 Numpy 中的方法、不過(guò)它留給我們的接口可能會(huì)稍微有些不一樣。以“求和”操作為例：

# 用 Numpy 數(shù)組進(jìn)行 Tensor 的初始化

x = tf.constant(np.array([[1, 2], [3, 4]]))

# Tensorflow 中對(duì)應(yīng)于 np.sum 的方法

axis0 = tf.reduce_sum(x, axis=0) # 將會(huì)得到值為 [ 4 6 ] 的 Tensor

axis1 = tf.reduce_sum(x, axis=1) # 將會(huì)得到值為 [ 3 7 ] 的 Tensor

更多的操作方法可以參見(jiàn)這里（https://zhuanlan.zhihu.com/p/26657869）

最后要特別指出的是，為了將 Graph 中的 Tensor 的值“提取”出來(lái)、我們需要定義一個(gè) Session 來(lái)做相應(yīng)的工作。可以這樣理解 Graph 和 Session 的關(guān)系（注：該理解可能有誤！如果我確實(shí)在瞎扯的話，歡迎觀眾老爺們指出 ( σ'ω')σ）：

Graph 中定義的是一套“運(yùn)算規(guī)則”

Session 則會(huì)“啟動(dòng)”這一套由 Graph 定義的運(yùn)算規(guī)則，而在啟動(dòng)的過(guò)程中、Session 可能會(huì)額外做三件事：

從運(yùn)算規(guī)則中提取出想要的中間結(jié)果

更新所有可訓(xùn)練的變量（如果啟動(dòng)的運(yùn)算規(guī)則包括“更新參數(shù)”這一步的話）

賦予“運(yùn)算規(guī)則”中一些“占位符”以具體的值

其中“更新參數(shù)”和“占位符”的相關(guān)說(shuō)明會(huì)放在后文進(jìn)行，這里我們只說(shuō)明“提取中間結(jié)果”是什么意思。比如現(xiàn)在 Graph 中有這么一套運(yùn)算規(guī)則：，而我只想要運(yùn)算規(guī)則被啟動(dòng)之后、y 的運(yùn)算結(jié)果。該需求的代碼實(shí)現(xiàn)如下：

x = tf.constant(1)

y = x + 1

z = y + 1

print(tf.Session().run(y)) # 將會(huì)輸出2

如果我想同時(shí)獲得 y 和 z 的運(yùn)算結(jié)果的話，只需將第 4 行改為如下代碼即可：

print(tf.Session().run([y, z])) # 將會(huì)輸出 [2, 3]

最后想要特別指出一個(gè)非常容易犯錯(cuò)的地方：當(dāng)我們使用了 Variable 時(shí)，必須要先調(diào)用初始化的方法之后、才能利用 Session 將相應(yīng)的值從 Graph 里面提取出來(lái)。比如說(shuō)，下面這段代碼是會(huì)報(bào)錯(cuò)的：

x = tf.Variable(1)

print(tf.Session().run(x)) # 報(bào)錯(cuò)！

應(yīng)該改為：

x = tf.Variable(1)

with tf.Session().as_default() as sess:

sess.run(tf.global_variables_initializer())

print(sess.run(x))

其中 tf.global_variables_initializer() 的作用可由其名字直接得知：初始化所有 Variable

接下來(lái)就是 LinearSVM 的實(shí)現(xiàn)了，由前文的討論可知，關(guān)鍵只在于把損失函數(shù)的形式表達(dá)出來(lái)（利用到了 ClassifierBase（https://link.zhihu.com/?target=https%3A//github.com/carefree0910/MachineLearning/blob/master/Util/Bases.py%23L196）；同時(shí)為了簡(jiǎn)潔，我們?cè)O(shè)置C=1）：

import tensorflow as tf

from Util.Bases import ClassifierBase

class TFLinearSVM(ClassifierBase):

def __init__(self):

super(TFLinearSVM, self).__init__()

self._w = self._b = None

# 使用 self._sess 屬性來(lái)存儲(chǔ)一個(gè) Session 以方便調(diào)用

self._sess = tf.Session()

def fit(self, x, y, sample_weight=None, lr=0.001, epoch=10 ** 4, tol=1e-3):

# 將 sample_weight（樣本權(quán)重）轉(zhuǎn)換為 constant Tensor

if sample_weight is None:

sample_weight = tf.constant(

np.ones(len(y)), dtype=tf.float32, name="sample_weight")

else:

sample_weight = tf.constant(

np.array(sample_weight) * len(y), dtype=tf.float32, name="sample_weight")

# 將輸入數(shù)據(jù)轉(zhuǎn)換為 constant Tensor

x, y = tf.constant(x, dtype=tf.float32), tf.constant(y, dtype=tf.float32)

# 將需要訓(xùn)練的 w、b 定義為可訓(xùn)練 Variable

self._w = tf.Variable(np.zeros(x.shape[1]), dtype=tf.float32, name="w")

self._b = tf.Variable(0., dtype=tf.float32, name="b")

# ========== 接下來(lái)的步驟很重要！！！ ==========

# 調(diào)用相應(yīng)方法獲得當(dāng)前模型預(yù)測(cè)值

y_pred = self.predict(x, True, False)

# 利用相應(yīng)函數(shù)計(jì)算出總損失：

# cost = ∑_(i=1)^N max?(1-y_i?(w?x_i+b),0)+1/2 + 0.5 * ‖w‖^2

cost = tf.reduce_sum(tf.maximum(

1 - y * y_pred, 0) * sample_weight) + tf.nn.l2_loss(self._w)

# 利用 Tensorflow 封裝好的優(yōu)化器定義“更新參數(shù)”步驟

# 該步驟會(huì)調(diào)用相應(yīng)算法、以減少上述總損失為目的來(lái)進(jìn)行參數(shù)的更新

train_step = tf.train.AdamOptimizer(learning_rate=lr).minimize(cost)

# 初始化所有 Variable

self._sess.run(tf.global_variables_initializer())

# 不斷調(diào)用“更新參數(shù)”步驟；如果期間發(fā)現(xiàn)誤差小于閾值的話就提前終止迭代

for _ in range(epoch):

# 這種寫(xiě)法是比較偷懶的寫(xiě)法，得到的 cost 將不太精確

if self._sess.run([cost, train_step])[0] < tol:

break

然后就要定義獲取模型預(yù)測(cè)值的方法——self.predict 了：

def predict(self, x, get_raw_results=False, out_of_sess=True):

# 利用 reduce_sum 方法算出預(yù)測(cè)向量

rs = tf.reduce_sum(self._w * x, axis=1) + self._b

if not get_raw_results:

rs = tf.sign(rs)

# 如果 out_of_sess 參數(shù)為 True、就要利用 Session 把具體數(shù)值算出來(lái)

if out_of_sess:

rs = self._sess.run(rs)

# 否則、直接把 Tensor 返回即可

return rs

之所以要額外用一個(gè) out_of_sess 參數(shù)控制輸出的原因如下：

Tensorflow 在內(nèi)部進(jìn)行 Graph 運(yùn)算時(shí)是無(wú)需把具體數(shù)值算出來(lái)的、不如說(shuō)使用原生態(tài)的 Tensor 進(jìn)行運(yùn)算反而會(huì)快很多

當(dāng)模型訓(xùn)練完畢后，在測(cè)試階段我們希望得到的當(dāng)然是具體數(shù)值而非 Tensor、此時(shí)就需要 Session 幫我們把中間結(jié)果提取出來(lái)了

以上就是 LinearSVM 的完整實(shí)現(xiàn)，可以看到還是相當(dāng)簡(jiǎn)潔的

這里特別指出這么一點(diǎn)：利用 Session 來(lái)提取中間結(jié)果這個(gè)過(guò)程并非是沒(méi)有損耗的；事實(shí)上，當(dāng) Graph 運(yùn)算本身的計(jì)算量不大時(shí)，開(kāi)啟、關(guān)閉 Session 所造成的開(kāi)銷(xiāo)反而會(huì)占整體開(kāi)銷(xiāo)中的絕大部分。因此在我們編寫(xiě) Tensorflow 程序時(shí)、要注意避免由于貪圖方便而隨意開(kāi)啟 Session

在本文的最后，我們來(lái)看一下 Tensorflow 里面 Placeholder 這個(gè)東西的應(yīng)用。目前實(shí)現(xiàn)的 LinearSVM 雖說(shuō)能用，但其實(shí)存在著內(nèi)存方面的隱患。為了解決這個(gè)隱患，一個(gè)常見(jiàn)的做法是分 Batch 訓(xùn)練，這將會(huì)導(dǎo)致“更新參數(shù)”步驟每次接受的數(shù)據(jù)都是“不固定”的數(shù)據(jù)——原數(shù)據(jù)的一個(gè)小 Batch。為了描述這個(gè)“不固定”的數(shù)據(jù)、我們就需要利用到 Tensorflow 中的“占位符（Placeholder）”，其用法非常直觀：

# 定義一個(gè)數(shù)據(jù)類型為 tf.float32、“長(zhǎng)”未知、“寬”為 2 的矩陣

Placeholder x = tf.placeholder(tf.float32, [None, 2])

# 定義一個(gè) numpy 數(shù)組：[ [ 1 2 ], [ 3 4 ], [ 5 6 ] ]

y = np.array([[1, 2], [3, 4], [5, 6]])

# 定義 x + 1 對(duì)應(yīng)的 Tensor

z = x + 1

# 利用 Session 及其 feed_dict 參數(shù)、將 y 的值賦予給 x、同時(shí)輸出 z 的值 print(tf.Session().run(z, feed_dict={x: y}))

# 將會(huì)輸出 [ [ 2 3 ], [ 4 5 ], [ 6 7 ] ]

于是分 Batch 運(yùn)算的實(shí)現(xiàn)步驟就很清晰了：

把計(jì)算損失所涉及的所有 x、y 定義為占位符

每次訓(xùn)練時(shí)，通過(guò) feed_dict 參數(shù)、將原數(shù)據(jù)的一個(gè)小 Batch 賦予給 x、y

占位符還有許多其它有趣的應(yīng)用手段，它們的思想都是相通的：將未能確定的信息以 Placeholder 的形式進(jìn)行定義、在確實(shí)調(diào)用到的時(shí)候再賦予具體的數(shù)值

事實(shí)上，基本所有 Tensorflow 模型都要用到 Placeholder。雖然我們上面實(shí)現(xiàn)的 TFLinearSVM 沒(méi)有用到，但正因如此、它是存在巨大缺陷的（比如說(shuō)，如果在同一段代碼中不斷地調(diào)用參數(shù) out_of_sess 為 True 的 predict 方法的話，會(huì)發(fā)現(xiàn)它的速度越來(lái)越慢。觀眾老爺們可以思考一下這是為什么 ( σ'ω')σ）

以上就是 Tensorflow 的一個(gè)簡(jiǎn)要教程，雖然我是抱著“即使從來(lái)沒(méi)用過(guò) Tensorflow 也能看懂”的心去寫(xiě)的，但可能還是會(huì)有地方說(shuō)得不夠詳細(xì)；若果真如此，還愿不吝指出 ( σ'ω')σ