和DeepMind數據科學家、Udacity深度學習導師Andrew Trask一起，基于Numpy手寫神經網絡，更深刻地理解反向傳播這一概念。

總結：基于可以嘗試和修改的玩具代碼，我能取得最好的學習效果。本教程基于一個非常簡單的玩具樣例（簡短的Python代碼實現）介紹反向傳播這一概念。

如果你對我的文章感興趣，歡迎在推特上關注 電子說，也歡迎給我反饋。

直接給我代碼

1. X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])

2. y = np.array([[0,1,1,0]]).T

3. syn0 =2*np.random.random((3,4)) -1

4. syn1 =2*np.random.random((4,1)) -1

5. forjinxrange(60000):

6. l1 =1/(1+np.exp(-(np.dot(X,syn0))))

7. l2 =1/(1+np.exp(-(np.dot(l1,syn1))))

8. l2_delta = (y - l2)*(l2*(1-l2))

9. l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))

10. syn1 += l1.T.dot(l2_delta)

11. syn0 += X.T.dot(l1_delta)

其他語言：D、C++、CUDA

不過，上面的代碼有點過于凝練了……讓我們循序漸進。

一、微型玩具網絡

基于反向傳播的神經網絡嘗試通過輸入來預測輸出。

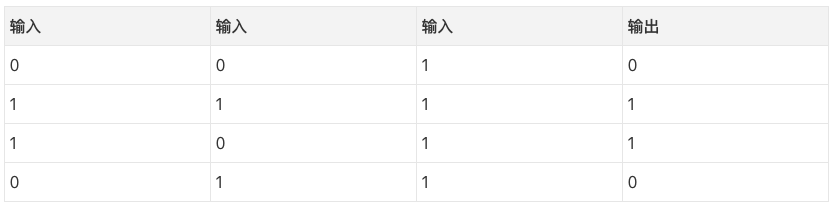
嘗試通過上表的輸入預測輸出。我們可以通過測量輸入值和輸出值的統計數據來解決這一問題。如果我們這么干，我們會發現最左邊的輸入和輸出完全相關（perfectly correlated）。最簡單形式的反向傳播，就是通過類似的測量統計數據的方式來建立模型。

雙層神經網絡

1. importnumpyasnp

3. # sigmoid函數

4. defnonlin(x,deriv=False):

5. if(deriv==True):

6. returnx*(1-x)

7. return1/(1+np.exp(-x))

9. # 輸入數據集

10. X = np.array([ [0,0,1],

11. [0,1,1],

12. [1,0,1],

13. [1,1,1] ])

15. # 輸出數據集

16. y = np.array([[0,0,1,1]]).T

18. # 設置隨機數種子使計算結果是確定的

19. # （實踐中這是一個很好的做法）

20. np.random.seed(1)

22. # 隨機初始化權重（均值0）

23. syn0 =2*np.random.random((3,1)) -1

25. foriterinxrange(10000):

27. # 前向傳播

28. l0 = X

29. l1 = nonlin(np.dot(l0,syn0))

31. # 差多少？

32. l1_error = y - l1

34. # 誤差乘以sigmoid在l1處的斜率

35. l1_delta = l1_error * nonlin(l1,True)

37. # 更新權重

38. syn0 += np.dot(l0.T,l1_delta)

40. print"訓練后輸出："

41. printl1

1. 訓練后輸出：

2. [[0.00966449]

3. [0.00786506]

4. [0.99358898]

5. [0.99211957]]

如你所見，“訓練后輸出："下面打印出的結果說明這一網絡是有效的！！！在我描述這個過程之前，我建議你嘗試探索以上代碼以獲得一些它如何工作的感性認識。以上代碼應該可以在Jupyter Notebook中直接運行（或者你也可以以腳本的形式運行，但我強烈建議使用notebook）。下面是探索代碼的一些提示：

• 比較第一次迭代和最后一次迭代后的l1

• 查看nonlin函數定義。該函數給出一個概率作為輸出。

• 查看迭代過程中l1_error的值是如何改變的。

• 仔細看看第36行。這段代碼的奧秘主要藏在此處。

• 查看第39行。網絡中的一切是為這個操作準備的。

讓我們逐行討論代碼。

建議：在兩塊屏幕上打開本文，這樣你就可以一邊查看代碼，一邊閱讀文章了。我寫作下文的時候基本上就是這么做的。

01行：導入numpy。numpy是一個線性代數庫。這是我們唯一的依賴。

04行：這是我們的“非線性”。非線性可以有多種選擇，這里我們選用的是sigmoid. sigmoid函數將任何值映射到0到1之間的值。我們使用sigmoid將數字轉換為概率。sigmoid函數還有其他一些有利于訓練神經網絡的性質。

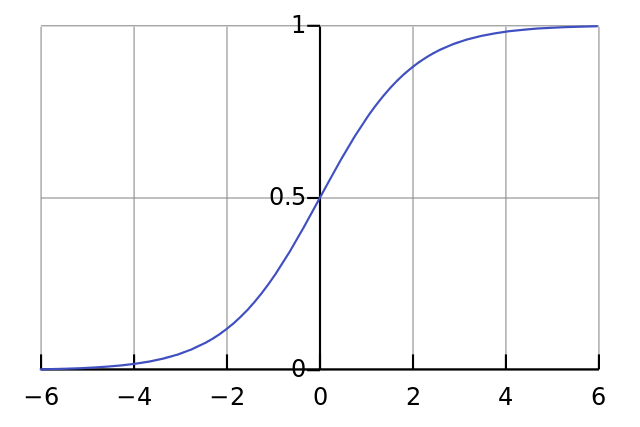
05行：注意這個函數同時可以生成sigmoid的導數（當deriv=True時）。sigmoid函數有一個非常棒的特性是它的輸出可以用來創建它的導數。如果sigmoid的輸出是變量out的話，它的導數是out * (1 - out)，非常高效。

如果你不熟悉導數，只需把它想象成sigmoid函數在給定的點上的斜率（如上圖所示，不同點的斜率不同）。想要了解更多關于導數的知識，可以參考Khan Academy的導數教程。

10行：初始化輸入數據集為numpy矩陣。每行是一個“訓練樣本”。每列對應一個輸入節點。因此，我們有3個輸入節點和4個訓練樣本。

16行：初始化輸出數據集。這里，我水平地生成了數據集（1行4列），以節省字符。.T是轉置函數。轉置之后，y矩陣有4行1列。和輸入一樣，每行是一個訓練樣本，每列（僅有一列）是一個輸出節點。所以，我們的網絡有3個輸入和1個輸出。

20行：設置隨機數種子是一個很好的做法。數字仍然是隨機分布的，但它們在每次訓練中將以完全一致的方式隨機分布。這更便于觀察你的改動對網絡的影響。

23行：這是神經網絡的權重矩陣。它命名為syn0，意味著它是“突觸（synapse）零”。由于我們的網絡只有兩層（輸入和輸出），我們只需要一個權重矩陣就可以連接兩者。它的維度是(3, 1)，因為我們有3個輸入和1個輸出。另一種看待它的方式是l0的尺寸是3，l1的尺寸是1. 我們需要將l0中的每個節點連接到l1中的每個節點，因而我們需要一個維度(3, 1)的矩陣。

同時注意，隨機初始化時的均值為零。權重初始化有不少理論。就目前而言，可以簡單地把這一做法（權重初始化均值為零）看成是最佳實踐。

另外需要注意的是，“神經網絡”實際上就是這個矩陣。我們有神經網絡層l0和l1，但它們其實是基于數據集創建的短暫值。我們并不保存它們。所有的學習所得都儲存在syn0矩陣中。

25行：網絡訓練代碼從這里開始。這是一個“迭代”訓練代碼的for循環，優化網絡以擬合數據集。

28行：第一層網絡l1直接就是數據。因此我們在這里明確聲明這一點。還記得X包含4個訓練樣本（行）嗎？在這一實現中，我們將同時處理所有樣本。這被稱為“全batch”（full batch）訓練。因此，我們有4個不同的l0行，但是如有必要，我們可以將它看成一個單獨的訓練樣本。在這里這些沒有區別。（如果需要，我們可以加載1000甚至10000行數據，而不用修改任何代碼）。

29行：這是我們的預測步驟。基本上，我們首先讓網絡“嘗試”基于輸入預測輸出。我們接著研究它的表現，從而加以調整，讓它在下一個迭代中表現更好。

這一行包含兩小步。首先矩陣l0和syn0相乘。接著將輸出傳給sigmoid函數。算下維度：

1. (4x3) dot (3x1) = (4x1)

矩陣乘法是有序的，滿足等式兩邊的維度必須一致。因此最終生成的矩陣的行數等于第一個矩陣的行數，列數等于第二個矩陣的列數。

由于我們載入了4個訓練樣本，我們最終對正確答案做了4次猜測，一個(4 x 1)矩陣。每個輸出對應與網絡對給定輸入的猜測。也許讀到這里你能很直觀地理解為什么我們之前說如有必要可以載入任意數目的訓練樣本，因為矩陣乘法仍然可以工作。

32行：好了，l1根據每個輸入作出了“猜測”。我們可以通過從猜測（l1）中減去真實答案（y）來看看它的表現如何。l1_error只是一個由正數和負數組成的向量，反映了網絡離正確還差多少。

36行：現在是關鍵時刻！這是整個模型的奧秘所在！這一行里發生了很多事情，所以讓我們進一步把它分成兩部分。

第一部分：導數

1. nonlin(l1,True)

如果l1表示下圖中的三點，那么上面的代碼生成了下圖曲線的斜率。注意，像x=2.0這樣很高的值（綠點）和像x=-1.0這樣很低的值（紫點）具有相對平緩的斜率。x=0（藍點）處的斜率最高。這起到了非常重要的作用。同時注意所有的導數都在0和1之間。

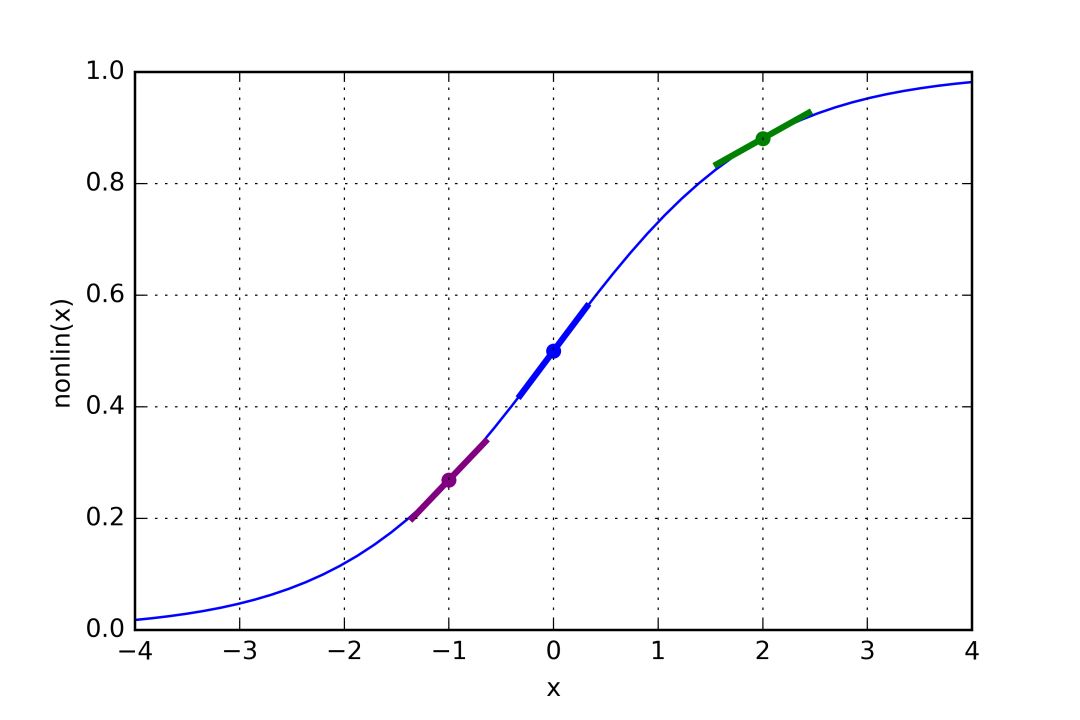
整個語句：誤差加權導數

1. l1_delta = l1_error * nonlin(l1,True)

“誤差加權導數”有數學上更精確的說法，但我覺得這個名字捕捉到了背后的直覺。l1_error是一個(4,1)矩陣。nonlin(l1, True)返回一個(4,1)矩陣。我們將它們逐元素相乘。這返回一個(4,1)矩陣l1_delta。

當我們將“斜率”乘以錯誤時，我們降低高信度預測的錯誤。再看一遍sigmoid圖像！如果斜率實在很平緩（接近0），那么這個網絡或者具有一個非常高的值，或者具有一個非常低的值。這意味著網絡十分自信。然而，如果網絡猜測的值接近(x=0, y=0.5)，那么它不是那么自信。我們更劇烈地更新那些缺乏信心的預測，同時傾向于通過乘以一個接近零的數字保留那些自信的預測。

行39：一切就緒，我們可以更新網絡了！讓我們看下單個訓練樣本。

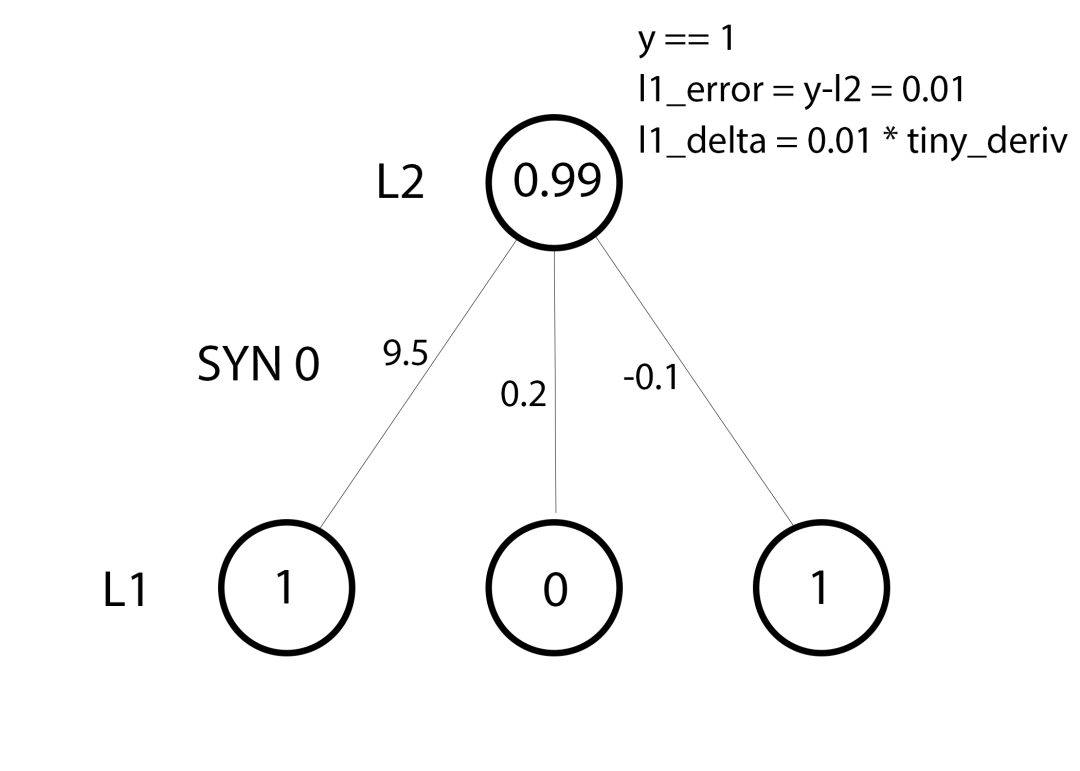
對這個樣本而言，我們已經準備好更新權重了。讓我們更新最左邊的權重（9.5）。

1. weight_update = input_value * l1_delta

對最左邊的權重而言，這將是1.0 * L1_delta。推測起來，這會非常輕微地增加9.5. 為什么只增加一點點？好吧，預測已經相當自信了，而且預測的結果也基本正確。低誤差和低斜率意味著非常小的更新。考慮所有3個權重。這3個權重都將略微增加。

然而，因為我們使用“全batch”配置，我們將對所有4個訓練樣本執行上述操作。因此，這個過程更像上圖所示。所以，第39行做了什么？它為每個訓練樣本的每個權重計算權重更新，累加起來，然后更新權重，這些都是在一行之內完成的。探索矩陣乘法，你將看到它是如何做到的！

奧秘

所以，既然我們已經了解網絡是如何更新的，讓我們回過頭來看一下訓練數據然后反思一下。當輸入和輸出都是1的時候，我們增加兩者之間的權重。當輸入是1、輸出是0時，我們減少兩者之間的權重。

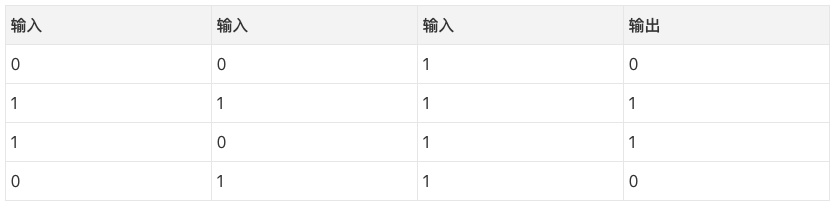
因此，在上表的4個訓練樣本中，第一個輸入與輸出之間的權重將持續增加或保持不變，而其他兩個權重將發現自己在不同的樣本上一會兒增加，一會兒下降（因而無法取得進展）。這一現象導致我們的網絡基于輸入和輸出之間的相關性進行學習。

二、稍微加大難度

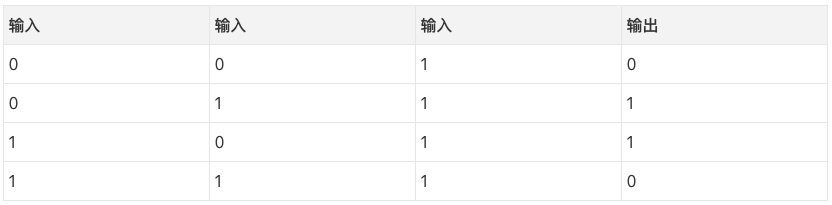
考慮基于三個輸入欄預測輸出欄。妙在沒有一列和輸出是相關的。每列有50%的機會預測1，50%的機會預測0.

那么，模式是什么呢？看起來結果完全和第三列無關，這一列的值永遠是1. 然而，第1列和第2列組合起來看比較清楚。如果第1列和第2列有一列是1（但兩列不同為1！），那么輸出是1. 這是我們的模式。

這被認為是一個“非線性”模式，因為輸入和輸出之間沒有直接的一一對應關系。相反，存在輸入的組合和輸出的一一對應關系，也就是第1列和第2列。

不管你信不信，圖像識別是一個類似的問題。如果有100張尺寸相同的煙斗和自行車的圖像，沒有任何單獨的像素位置和自行車或煙斗的存在性直接相關。從純統計學角度看，像素可能是隨機的。然而，特定的像素組合不是隨機的，也就是說，像素的組合形成了自行車或煙斗的圖像。

我們的策略

為了將我們的像素組合成和輸出具有一一對應關系的東西，我們需要增加一個網絡層。我們的第一層網絡將組合輸入，第二層網絡以第一層網絡的輸出作為輸入，并將其輸入映射到輸出。在我們跳到實現之前，先看下這個表格。

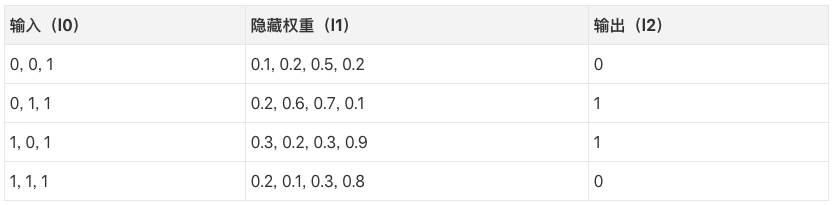
如果我們隨機初始化權重，我們將得到如上表所示的l1的隱藏狀態值。注意到沒有？隱藏權重的第二項（第二個隱藏節點）與輸出已經有隱約的相關性！它并不完美，但確實存在。信不信由你，這是神經網絡訓練中很重要的一部分。（一個有爭議的觀點認為這是神經網絡訓練的唯一方式。）下面的訓練將放大這一相關性。它將同時更新syn1和syn0，更新syn1以便將隱藏權重映射到輸出，更新syn0以便更好地基于輸入產生權重！

注意：這個增加更多網絡層以建模關系的更多組合的領域稱為“深度學習”，得名自建模時采用的越來越深的網絡層。

三層神經網絡

1. importnumpyasnp

3. defnonlin(x,deriv=False):

4. if(deriv==True):

5. returnx*(1-x)

7. return1/(1+np.exp(-x))

9. X = np.array([[0,0,1],

10. [0,1,1],

11. [1,0,1],

12. [1,1,1]])

14. y = np.array([[0],

15. [1],

16. [1],

17. [0]])

19. np.random.seed(1)

21. # 隨機初始化權重（均值0）

22. syn0 =2*np.random.random((3,4)) -1

23. syn1 =2*np.random.random((4,1)) -1

25. forjinxrange(60000):

27. # 前向傳播，層0、1、2

28. l0 = X

29. l1 = nonlin(np.dot(l0,syn0))

30. l2 = nonlin(np.dot(l1,syn1))

32. # 離目標值還差多少？

33. l2_error = y - l2

35. if(j%10000) ==0:

36. print"Error:"+ str(np.mean(np.abs(l2_error)))

38. # 目標值在哪個方向？

39. # 我們很確定嗎？如果確定，不要改變太多。

40. l2_delta = l2_error*nonlin(l2,deriv=True)

42. # 根據權重 ，每個l1值對l2誤差的貢獻有多大？

43. l1_error = l2_delta.dot(syn1.T)

45. # 目標l1在哪個方向？

46. # 我們很確定嗎？如果確定，不要改變太多。

47. l1_delta = l1_error * nonlin(l1,deriv=True)

49. syn1 += l1.T.dot(l2_delta)

50. syn0 += l0.T.dot(l1_delta)

1. Error:0.496410031903

2. Error:0.00858452565325

3. Error:0.00578945986251

4. Error:0.00462917677677

5. Error:0.00395876528027

6. Error:0.00351012256786

建議：在兩塊屏幕上打開本文，這樣你就可以一邊查看代碼，一邊閱讀文章了。我寫作下文的時候基本上就是這么做的。

所有的一切看起來應該很相似！這其實就是將2個之前的實現堆疊在一起。l1的輸出是l2的輸入。唯一不同的是第43行。

行43：使用l2的“信度加權誤差”來確立l1的誤差。為了做到這一點，它簡單地將權重間的誤差從l2傳給l1. 你可以把它的結果叫作“貢獻加權誤差”，因為我們學習l1中的每個節點對l2中的誤差的“貢獻”有多少。這一步驟稱為“反向傳播”，算法也是因此得名的。我們接著更新syn0，正如我們在雙層實現中所做的那樣。

三、結語和以后的工作

我的建議

如果你對神經網絡的態度是嚴肅的，那我有一個建議。嘗試基于回憶重建這個網絡。我知道這也許聽起來有點瘋狂，但它切切實實很有幫助。如果你希望能夠根據最新的學術論文創建任意的神經網絡架構，或者閱讀和理解不同架構的代碼樣例，我認為這是一個殺手級練習。即使你使用Torch、Caffe、Theano之類的框架，我仍然認為這是有用的。我在進行這一練習之前和神經網絡打過好多年交道，這個練習是我在這一領域所做的最好的投資（而且它花不了多久）。

以后的工作

這個玩具例子仍然需要一些掛件才能真正解決當前最先進的架構。如果你打算進一步改進你的網絡，下面是一些值得了解的概念。（也許我以后的文章會涉及其中部分內容。）

• Alpha

• Bias Units（偏置單元）

• Mini-Batches

• Delta Trimming

• Parameterized Layer Sizes（參數化的層尺寸）

• Regularization（正則化）

• Dropout

• Momentum（動量）

• Batch Normalization

• GPU兼容性

• 其他酷炫特性