感知機是個相當簡單的模型，但它既可以發展成支持向量機（通過簡單地修改一下損失函數）、又可以發展成神經網絡（通過簡單地堆疊），所以它也擁有一定的地位

為方便，我們統一討論二分類問題，并將兩個類別的樣本分別稱為正、負樣本

感知機能做什么？

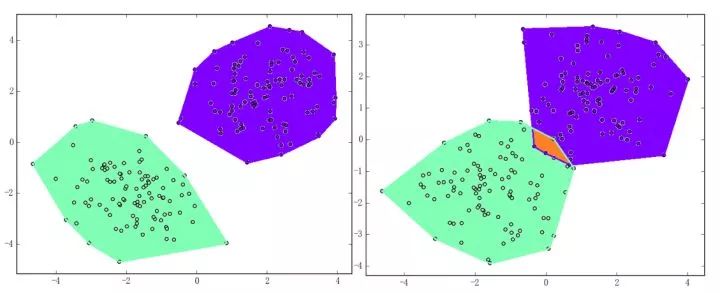
感知機能（且一定能）將線性可分的數據集分開。什么叫線性可分？在二維平面上、線性可分意味著能用一條線將正負樣本分開，在三維空間中、線性可分意味著能用一個平面將正負樣本分開。可以用兩張圖來直觀感受一下線性可分（上圖）和線性不可分（下圖）的概念：

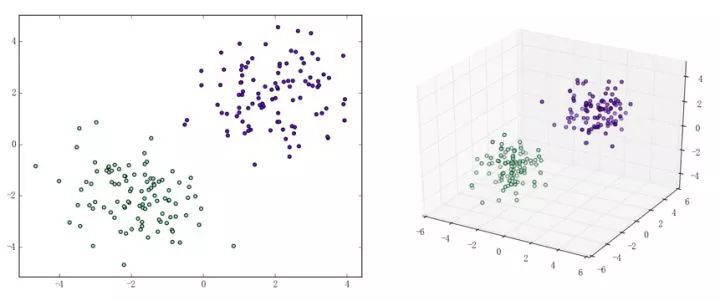
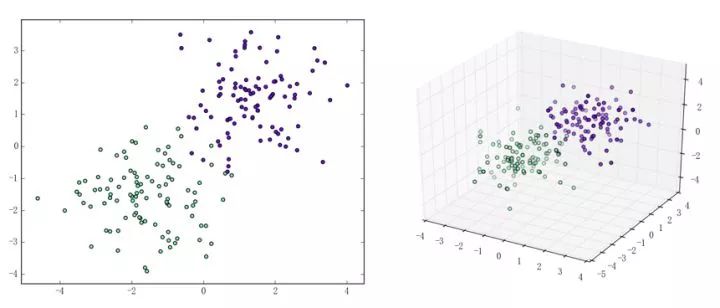
那么一個感知機將會如何分開線性可分的數據集呢？下面這兩張動圖或許能夠給觀眾老爺們一些直觀感受：

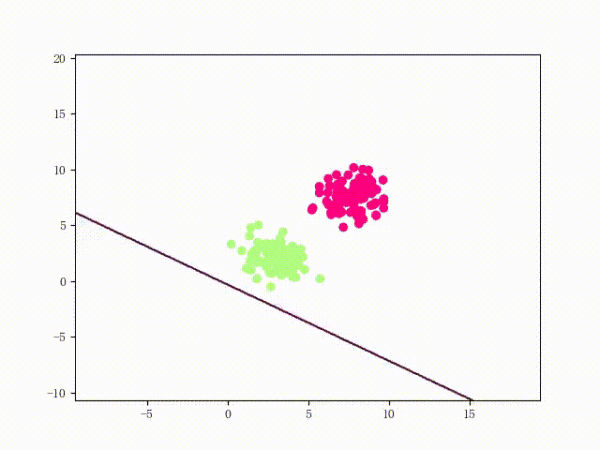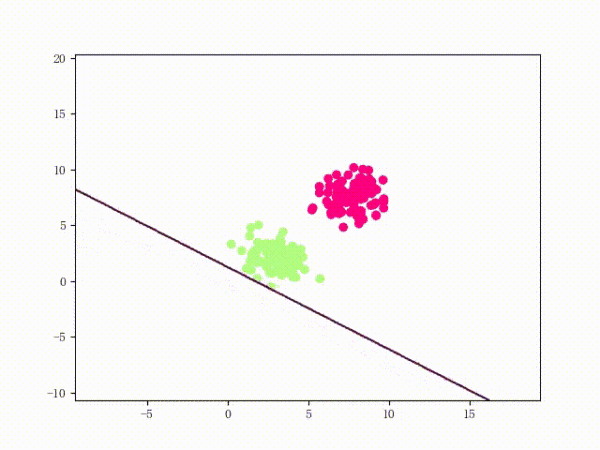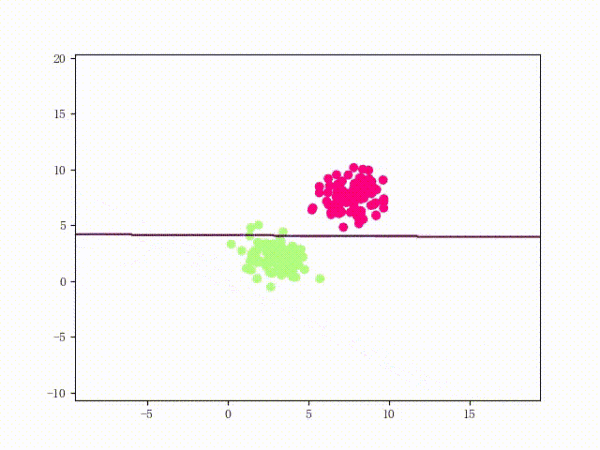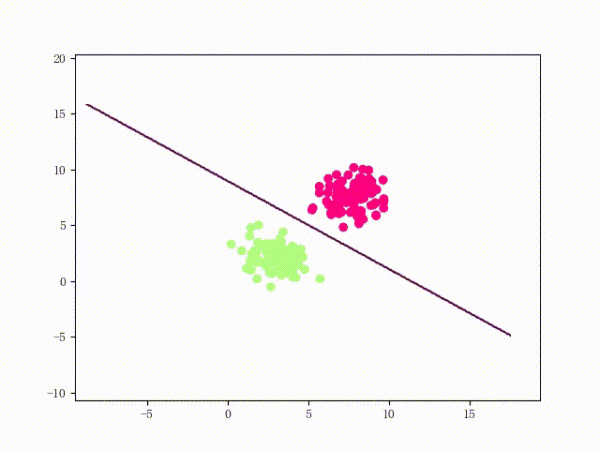
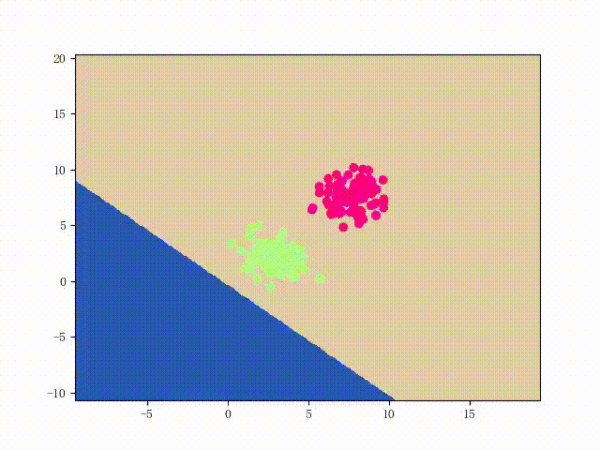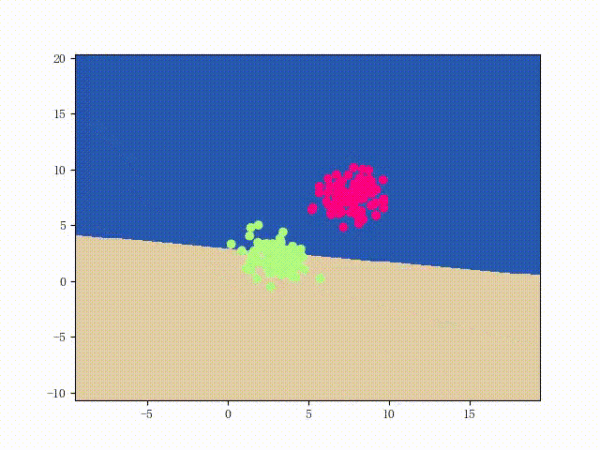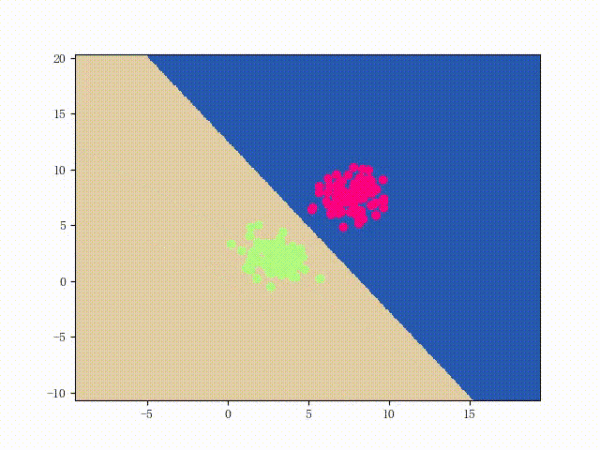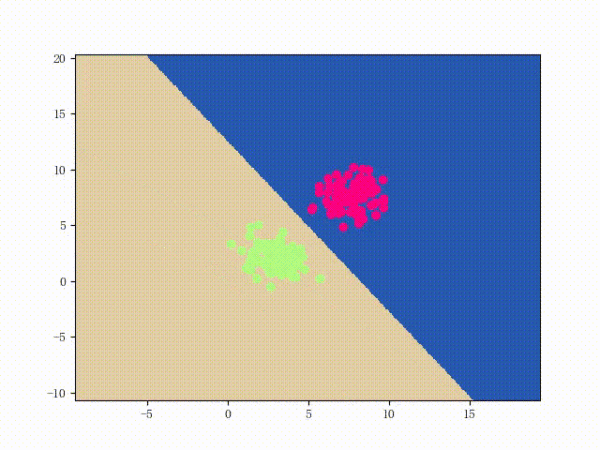
看上去挺捉急的，不過我們可以放心的是：只要數據集線性可分，那么感知機就一定能“蕩”到一個能分開數據集的地方（文末會附上證明）

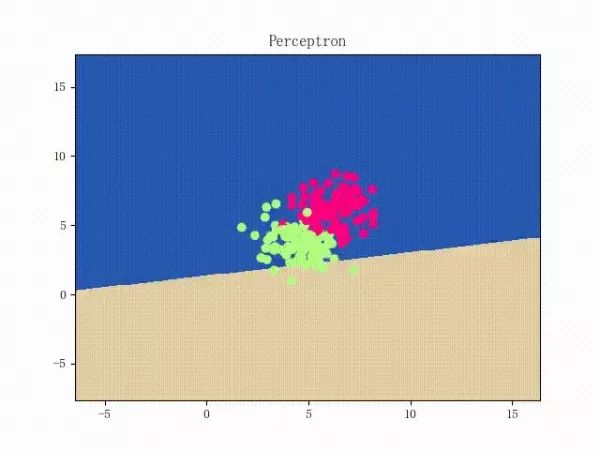
那么反過來，如果數據集線性不可分，那么感知機將如何表現？相信聰明的觀眾老爺們已經猜到了：它將會一直“蕩來蕩去”（最后停了是因為到了迭代上限）（然后貌似動圖太大導致有殘影……不過效果也不差所以就將就著看一下吧 ( σ'ω')σ）：

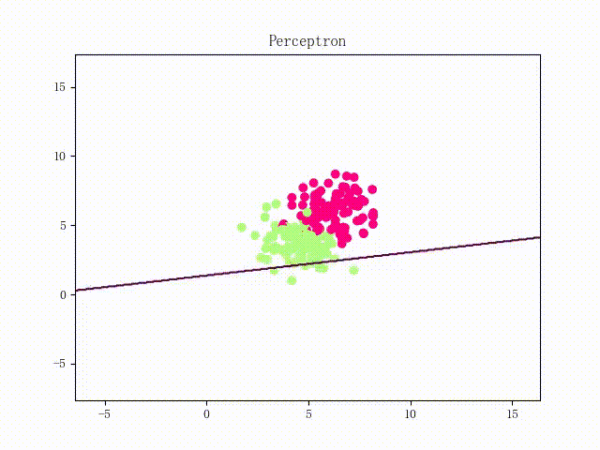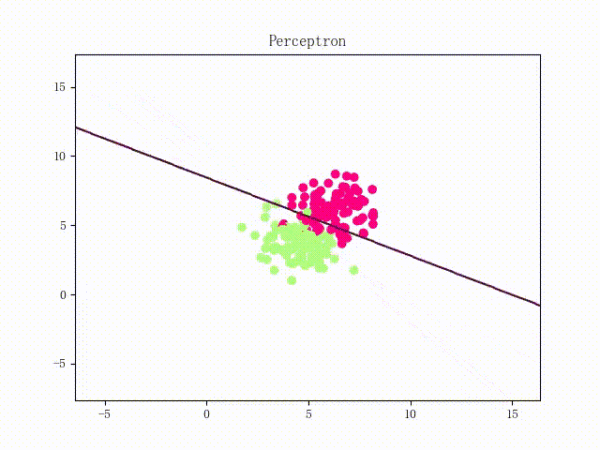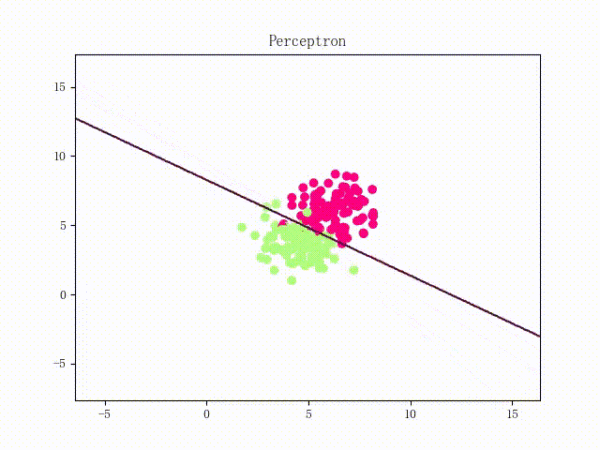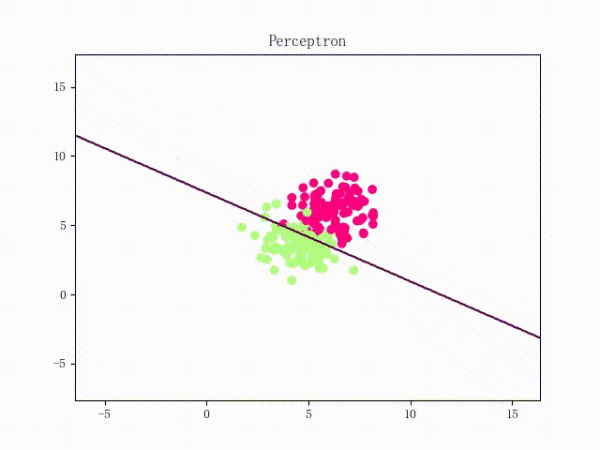
class Perceptron: def __init__(self): self._w = self._b = None def fit(self, x, y, lr=0.01, epoch=1000): # 將輸入的 x、y 轉為 numpy 數組 x, y = np.asarray(x, np.float32), np.asarray(y, np.float32) self._w = np.zeros(x.shape[1]) self._b = 0.

上面這個 fit 函數中有個 lr 和 epoch，它們分別代表了梯度下降法中的學習速率和迭代上限（p.s. 由后文的推導我們可以證明，對感知機模型來說、其實學習速率不會影響收斂性【但可能會影響收斂速度】）

梯度下降法我們都比較熟悉了。簡單來說，梯度下降法包含如下兩步：

求損失函數的梯度（求導）

梯度是函數值增長最快的方向我們想要最小化損失函數我們想讓函數值減少得最快將參數沿著梯度的反方向走一步

（這也是為何梯度下降法有時被稱為最速下降法的原因。梯度下降法被普遍應用于神經網絡、卷積神經網絡等各種網絡中，如有興趣、可以參見這篇文章(https://zhuanlan.zhihu.com/p/24540037)）

那么對于感知機模型來說，損失函數是什么呢？注意到我們感知機對應的超平面為

for _ in range(epoch): # 計算 w·x+b y_pred = x.dot(self._w) + self._b # 選出使得損失函數最大的樣本 idx = np.argmax(np.maximum(0, -y_pred * y)) # 若該樣本被正確分類，則結束訓練 if y[idx] * y_pred[idx] > 0: break # 否則，讓參數沿著負梯度方向走一步 delta = lr * y[idx] self._w += delta * x[idx] self._b += delta

那么一個感知機將會如何分開線性可分的數據集呢？下面這兩張動圖或許能夠給觀眾老爺們一些直觀感受：

至此，感知機模型就大致介紹完了，剩下的則是一些純數學的東西，大體上不看也是沒問題的（趴

相關數學理論

亦即訓練步數是有上界的，這意味著收斂性。而且中不含學習速率，這說明對感知機模型來說、學習速率不會影響收斂性

最后簡單介紹一個非常重要的概念：拉格朗日對偶性（Lagrange Duality）。我們在前三小節介紹的感知機算法，其實可以稱為“感知機的原始算法”；而利用拉格朗日對偶性，我們可以得到感知機算法的對偶形式。鑒于拉格朗日對偶性的原始形式太過純數學，所以我打算結合具體的算法來介紹、而不打算敘述其原始形式，感興趣的觀眾老爺可以參見這里（https://en.wikipedia.org/wiki/Duality_(optimization)）

在有約束的最優化問題中，為了便于求解、我們常常會利用它來將比較原始問題轉化為更好解決的對偶問題。對于特定的問題，原始算法的對偶形式也常常會有一些共性存在。比如對于感知機和后文會介紹的支持向量機來說，它們的對偶算法都會將模型的參數表示為樣本點的某種線性組合、并把問題轉化為求解線性組合中的各個系數

雖說感知機算法的原始形式已經非常簡單，但是通過將它轉化為對偶形式、我們可以比較清晰地感受到轉化的過程，這有助于理解和記憶后文介紹的、較為復雜的支持向量機的對偶形式

考慮到原始算法的核心步驟為：

此即感知機模型的對偶形式。需要指出的是，在對偶形式中、樣本點里面的x僅以內積的形式（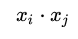

注意到對偶形式的訓練過程常常會重復用到大量的、樣本點之間的內積，我們通常會提前將樣本點兩兩之間的內積計算出來并存儲在一個矩陣中；這個矩陣就是著名的 Gram 矩陣、其數學定義即為：

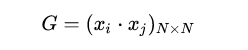
從而在訓練過程中如果要用到相應的內積、只需從 Gram 矩陣中提取即可，這樣在大多數情況下都能大大提高效率