電池管理系統,BMS(Battery Management System),是電動汽車動力電池系統的重要組成。它一方面檢測收集并初步計算電池實時狀態參數,并根據檢測值與允許值的比較關系控制供電回路的通斷;另一方面,將采集的關鍵數據上報給整車控制器,并接收控制器的指令,與車輛上的其他系統協調工作。電池管理系統,不同電芯類型,對管理系統的要求往往并不一樣。那么,一個典型的動力電池管理系統具體都需要關注哪些功能呢?今天翻譯整理了一篇文章,一起看看BMS的關鍵技術,整體內容分成上中下三個部分。
一個典型的動力電池管理系統,需要實現哪些功能(上篇)
1 簡介
電動汽車用鋰離子電池容量大、串并聯節數多,系統復雜,加之安全性、耐久性、動力性等性能要求高、實現難度大,因此成為影響電動汽車推廣普及的瓶頸。鋰離子電池安全工作區域受到溫度、電壓窗口限制,超過該窗口的范圍,電池性能就會加速衰減,甚至發生安全問題。目前,大部分車用鋰離子電池,要求的可靠工作溫度為,放電時-20~55°C,充電時0~45°C(對石墨負極),而對于負極LTO充電時最低溫度為-30°C;工作電壓一般為1.5~4.2 V左右(對于LiCoO2/C、LiNi0.8Co0.15Al0.05O2/C、LiCoxNiyMnzO2/C以及LiMn2O4/C等材料體系約2.5~4.2 V,對于LiMn2O4/Li4Ti5O12 材料體系約1.5~2.7 V,對于LiFePO4/C 材料體系約2.0~3.7 V)。
溫度對鋰電池性能尤其安全性具有決定性的影響,根據電極材料類型的不同,鋰電池(C/LiMn2O4 , C/LMO,C/LiCoxNiyMnzO2 ,C/NCM, C/LiFePO4 ,C/LiNi0.8Co0.15Al0.05O2, C/NCA)典型的工作溫度如下:放電在-20-55℃,充電在0-45℃;負極材料為Li4Ti5O12 或者 LTO時,最低充電溫度往往可以達到-30℃。
當溫度過高時,會給電池的壽命造成不利影響。當溫度高至一定程度,則可能造成安全問題。如圖所示圖1中,當溫度為90~120℃時,SEI膜將開始放熱分解[1~3],而一些電解質體系會在較低溫度下分解約69℃[4]。當溫度超過120℃,SEI膜分解后無法保護負碳電極 ,使得 負極與有機電解質直接反應,產生可燃氣體將[3]。當溫度為130℃,隔膜將開始熔化并關閉離子通道,使得電池的正負極暫時沒有電流流動[5,6]。當溫度升高時,正極材料開始分解(LiCoO2開始分解約在150℃[7],LiNi0.8Co0.15Al0.05O2在約160℃[8,9],LiNixCoyMnzO2 在約210℃[8],LiMn2O4 在約265℃ [1] ,LiFePO4在約310℃ [7])并產生氧氣。當溫度高于200℃時,電解液會分解并產生可燃性氣體[3],并且與由正極的分解產生的氧氣劇烈反應[9],進而導致熱失控。在0℃以下充電,會造成鋰金屬在負極表面形成電鍍層,這會減少電池的循環壽命。[10]
過低的電壓或者過放電,會導致電解液分解并產生可燃氣體進而導致潛在安全風險。過高的電壓或者過充電,可能導致正極材料失去活性,并產生大量的熱;普通電解質在電壓高于4.5 V時會分解[12]
為了解決這些問題,人們試圖開發能夠在非常惡劣的情況下進行工作的新電池系統,另一方面,目前商業化鋰離子電池必須連接管理系統,使鋰離子電池可以得到有效的控制和管理,每個單電池都在適當的條件下工作,充分保證電池的安全性、耐久性和動力性。
2 電池管理系統定義
電池管理系統的主要任務是保證電池系統的設計性能,可以分解成如下三個方面:
1)安全性,保護電池單體或電池組免受損壞,防止出現安全事故;
2)耐久性,使電池工作在可靠的安全區域內,延長電池的使用壽命;
3)動力性,維持電池工作在滿足車輛要求的狀態下。鋰離子電池的安全工作區域如圖1所示。
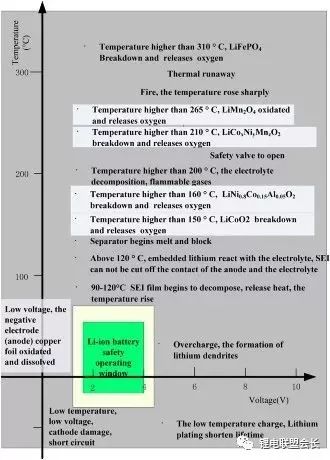
圖1為鋰離子電池的安全操作窗口
BMS由各類傳感器、執行器、控制器以及信號線等組成,為滿足相關的標準或規范,BMS應該具有以下功能。
1)電池參數檢測。包括總電壓、總電流、單體電池電壓檢測(防止出現過充、過放甚至反極現象)、溫度檢測(最好每串電池、關鍵電纜接頭等均有溫度傳感器)、煙霧探測(監測電解液泄漏等)、絕緣檢測(監測漏電)、碰撞檢測等。
2)電池狀態估計。包括荷電狀態(SOC)或放電深度(DOD)、健康狀態(SOH)、功能狀態(SOF)、能量狀態(SOE)、故障及安全狀態(SOS)等。
3)在線故障診斷。包括故障檢測、故障類型判斷、故障定位、故障信息輸出等。故障檢測是指通過采集到的傳感器信號,采用診斷算法診斷故障類型,并進行早期預警。電池故障是指電池組、高壓電回路、熱管理等各個子系統的傳感器故障、執行器故障(如接觸器、風扇、泵、加熱器等),以及網絡故障、各種控制器軟硬件故障等。電池組本身故障是指過壓(過充)、欠壓(過放)、過電流、超高溫、內短路故障、接頭松動、電解液泄漏、絕緣降低等。
4)電池安全控制與報警。包括熱系統控制、高壓電安全控制。BMS診斷到故障后,通過網絡通知整車控制器,并要求整車控制器進行有效處理(超過一定閾值時BMS也可以切斷主回路電源),以防止高溫、低溫、過充、過放、過流、漏電等對電池和人身的損害。
5)充電控制。BMS中具有一個充電管理模塊,它能夠根據電池的特性、溫度高低以及充電機的功率等級,控制充電機給電池進行安全充電。
6)電池均衡。不一致性的存在使得電池組的容量小于組中最小單體的容量。電池均衡是根據單體電池信息,采用主動或被動、耗散或非耗散等均衡方式,盡可能使電池組容量接近于最小單體的容量。
7)熱管理。根據電池組內溫度分布信息及充放電需求,決定主動加熱/散熱的強度,使得電池盡可能工作在最適合的溫度,充分發揮電池的性能。
8)網絡通訊。BMS需要與整車控制器等網絡節點通信;同時,BMS在車輛上拆卸不方便,需要在不拆殼的情況下進行在線標定、監控、自動代碼生成和在線程序下載(程序更新而不拆卸產品)等,一般的車載網絡均采用CAN總線技術。
9)信息存儲。用于存儲關鍵數據,如SOC、SOH、SOF、SOE、累積充放電Ah數、故障碼和一致性等。車輛中的真實BMS可能只有上面提到的部分硬件和軟件。每個電池單元至少應有一個電池電壓傳感器和一個溫度傳感器。對于具有幾十個電池的電池系統,可能只有一個BMS控制器,或者甚至將BMS功能集成到車輛的主控制器中。對于具有數百個電池單元的電池系統,可能有一個主控制器和多個僅管理一個電池模塊的從屬控制器。對于每個具有數十個電池單元的電池模塊,可能存在一些模塊電路接觸器和平衡模塊,并且從控制器像測量電壓和電流一樣管理電池模塊,控制接觸器,均衡電池單元并與主控制器通信。根據所報告的數據,主控制器將執行電池狀態估計,故障診斷,熱管理等。
10)電磁兼容。由于電動車使用環境惡劣,要求BMS具有好的抗電磁干擾能力,同時要求BMS對外輻射小。電動汽車BMS軟硬件的基本框架如圖2所示。
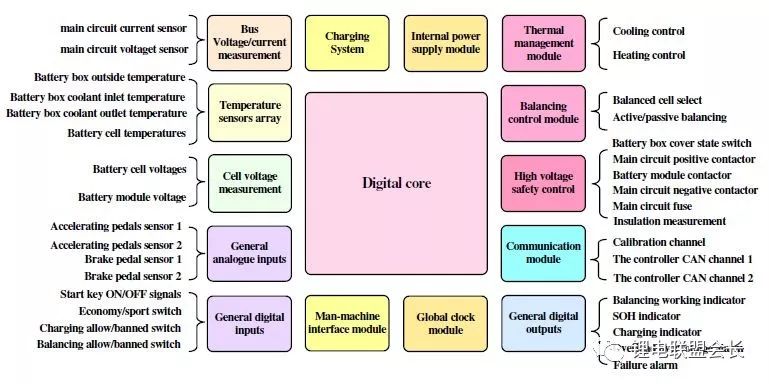
圖2車載BMS的軟硬件基本框架
3 BMS的關鍵問題
盡管BMS有許多功能模塊,本文僅分析和總結其關鍵問題。目前,關鍵問題涉及電池電壓測量,數據采樣頻率同步性,電池狀態估計,電池的均勻性和均衡,和電池故障診斷的精確測量。
3.1 電池電壓測量(CVM)
電池電壓測量的難點存在于以下幾個方面:
(1)電動汽車的電池組有數百個電芯的串聯連接,需要許多通道來測量電壓。由于被測量的電池電壓有累積電勢,而每個電池的積累電勢都不同,這使得它不可能采用單向補償方法消除誤差。
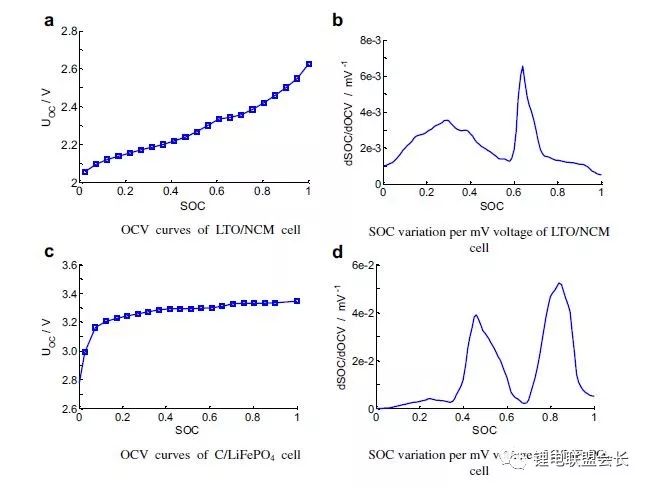
圖3OCV曲線和每毫伏電壓的SOC的變化(在25℃測量,休息時間3小時)
(2)電壓測量需要高精度(特別是對于C / LiFePO4電池)。SOC估算對電池電壓精度提出了很高的要求。這里我們以C / LFP和LTO / NCM型電池為例。圖3顯示了電池C / LiFePO4和LTO / NCM的開路電壓(OCV)以及每mV電壓對應的SOC變化。從圖中我們可以看到LTO / NCM的OCV曲線的斜率相對陡峭,且大多數SOC范圍內,每毫伏的電壓變化對應的最大SOC率范圍低于0.4%(除了SOC 60~70%)。因此,如果電池電壓的測量精度為10mV,那么通過OCV估計方法獲得的SOC誤差低于4%。因此,對于LTO / NCM電池,電池電壓的測量精度需要小于10 mV。但C / LiFePO4OCV曲線的斜率相對平緩,并且在大多數范圍內(除了SOC
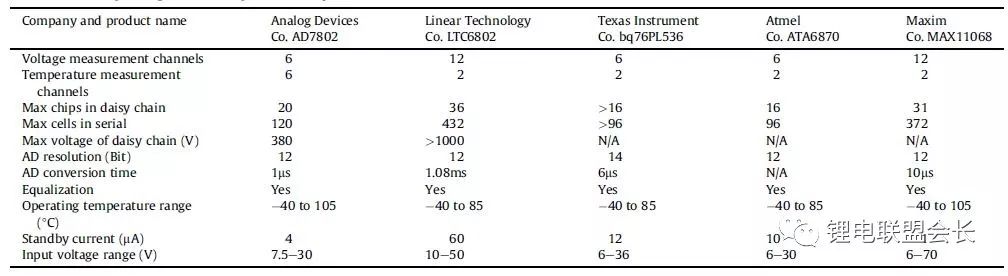
表1 統計電池管理和均衡芯片
3.2數據采樣頻率同步性
信號的采樣頻率與同步對數據實時分析和處理有影響。設計BMS時,需要對信號的采樣頻率和同步精度提出要求。但目前部分BMS設計過程中,對信號采樣頻率和同步沒有明確要求。電池系統信號有多種,同時電池管理系統一般為分布式,如果電流的采樣與單片電壓采樣分別在不同的電路板上;信號采集過程中,不同控制子板信號會存在同步問題,會對內阻的實時監測算法產生影響。同一單片電壓采集子板,一般采用巡檢方法,單體電壓之間也會存在同步問題,影響不一致性分析。系統對不同信號的數據采樣頻率和同步要求不同,對慣性大的參量要求較低,如純電動車電池正常放電的溫升數量級為1℃/10 min,考慮到溫度的安全監控,同時考慮BMS溫度的精度(約為1℃),溫度的采樣間隔可定為30 s(對混合動力電池,溫度采樣率需要更高一些)。
電壓與電流信號變化較快,采樣頻率和同步性要求很高。由交流阻抗分析可知,動力電池的歐姆內阻響應在ms級,SEI膜離子傳輸阻力電壓響應為10 ms級,電荷轉移(雙電容效應)響應為1~10 s級,擴散過程響應為min級。目前,電動車加速時,驅動電機的電流從最小變化到最大的響應時間約為0.5 s,電流精度要求為1%左右,綜合考慮變載工況的情況,電流采樣頻率應取10~200 Hz。單片信息采集子板電壓通道數一般為6 的倍數,目前最多為24 個。一般純電動乘用車電池由約100 節電池串聯組成,單體電池信號采集需要多個采集子板。為了保證電壓同步,每個采集子板中單體間的電壓采樣時間差越小越好,一個巡檢周期最好在25 ms內。子板之間的時間同步可以通過發送一幀CAN參考幀來實現。數據更新頻率應為10 Hz以上。
參考文獻


一個典型的動力電池管理系統,需要實現哪些功能(中篇)
上篇說到,鋰電池系統龐大,需要電池管理系統的監督和優化,以維護其安全性、耐久性和動力性。上篇中提及的BMS功能需求包括電池電壓測量、數據采樣頻率同步性。本文繼續,中篇講述溫度估計和SOC估計。預報,明天的下篇中會包括電池狀態包括SOH(健康狀態估計)、SOS(安全狀態估計)、SOF(功能狀態估計) 及SOE(可用能量狀態估計)。這些功能是期望BMS具備的,但實際應用中,出于客戶要求、車型要求以及成本等等的考慮,實際設計到系統中的可能只是其中的幾個。
3.3 電池狀態估計
電池狀態包括電池溫度、SOC(荷電狀態估計)、SOH(健康狀態估計)、SOS(安全狀態估計)、SOF(功能狀態估計) 及SOE(可用能量狀態估計)。各種狀態估計之間的關系如圖4所示。電池溫度估計是其他狀態估計的基礎,SOC 估計受到SOH 的影響,SOF 是由SOC、SOH、SOS 以及電池溫度共同確定的,SOE 則與SOC、SOH、電池溫度、未來工況有關。
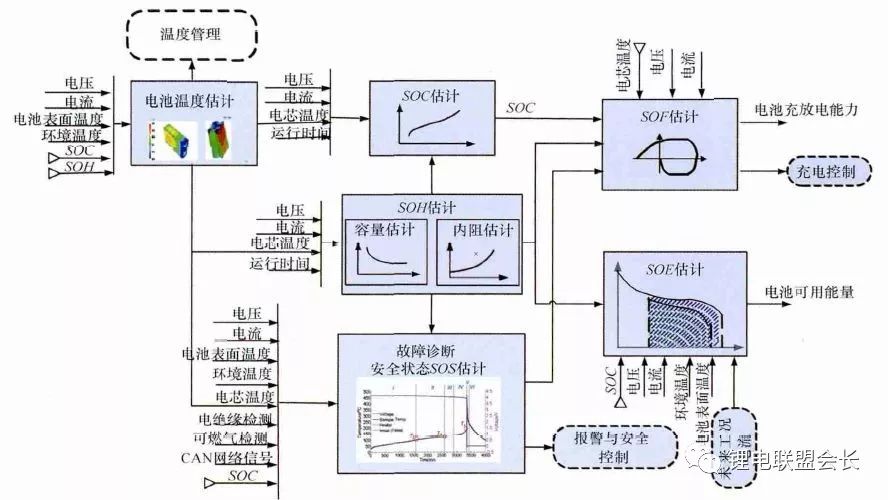
圖4. BMS狀態估計算法框架
3.3.1 電池溫度估計
溫度對電池性能影響較大,目前一般只能測得電池表面溫度,而電池內部溫度需要使用熱模型進行估計。常用的電池熱模型包括零維模型(集總參數模型)、一維乃至三維模型。零維模型可以大致計算電池充放電過程中的溫度變化,估計精度有限,但模型計算量小,因此可用于實時的溫度估計。一維、二維及三維模型需要使用數值方法對傳熱微分方程進行求解,對電池進行網格劃分,計算電池的溫度場分布,同時還需考慮電池結構對傳熱的影響(結構包括內核、外殼、電解液層等)。一維模型中只考慮電池在一個方向的溫度分布,在其他方向視為均勻。二維模型考慮電池在兩個方
向的溫度分布,對圓柱形電池來說,軸向及徑向的溫度分布即可反映電池內部的溫度場。二維模型一般用于薄片電池的溫度分析。三維模型可以完全反映方形電池內部的溫度場,仿真精度較高,因而研究較多。但三維模型的計算量大,無法應用于實時溫度估計,只能用于在實驗室中進行溫度場仿真。為了讓三維模型的計算結果實時應用,研究人員利用三維模型的溫度場計算結果,將電池產熱功率和內外溫差的關系用傳遞函數表達,通過產熱功率和電池表面溫度估計電池內部的溫度,具有在BMS中應用的潛力。圖5所示為電池內部溫度的估計流程。
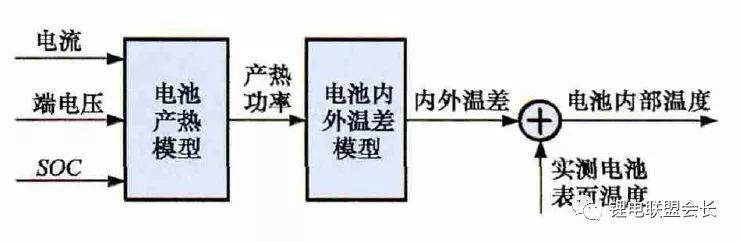
圖5 電池內部溫度估計流程
一般地,鋰離子電池適宜的工作溫度為15~35℃,而電動汽車的實際工作溫度為-30~50℃,因此必須對電池進行熱管理,低溫時需要加熱,高溫時需要冷卻。熱管理包括設計與控制兩方面,其中,熱管理設計不屬于本文內容。溫度控制是通過測溫元件測得電池組不同位置的溫度,綜合溫度分布情況,熱管理系統控制電路進行散熱,熱管理的執行部件一般有風扇、水/油泵、制冷機等。比如,可以根據溫度范圍進行分檔控制。Volt插電式混合動力電池熱管理分為3種模式:主動(制冷散熱)、被動(風扇散熱)和不冷卻模式,當動力電池溫度超過某預先設定的被動冷卻目標溫度后,被動散熱模式啟動;而當溫度繼續升高至主動冷卻目標溫度以上時,主動散熱模式啟動。
3.2 荷電狀態(SOC)估計
SOC(State of Charge),可用電量占據電池最大可用容量的比例,通常以百分比表示,100%表示完全充電,0%表示完全放電。
這是針對單個電池的定義,對于電池模塊(或電池組,由于電池組由多個模塊組成,因此從模塊SOC計算電池組的SOC就像電池電池單體SOC估計模塊SOC一樣),情況有一點復雜。在SOC估計方法的最后一節討論。
目前,對SOC 的研究已經基本成熟,SOC 算法主要分為兩大類,一類為單一SOC 算法,另一類為多種單一SOC 算法的融合算法。單一SOC 算法包括安時積分法、開路電壓法、基于電池模型估計的開路電壓法、其他基于電池性能的SOC估計法等。融合算法包括簡單的修正、加權、卡爾曼濾波(或擴展卡爾曼濾波)以及滑模變結構方法等。
1) 放電測試方法
確定電池SOC的最可靠方法是在受控條件下進行放電測試,即指定的放電速率和環境溫度。這個測試可以準確的計算電池的剩余電量SOC,但所消耗的時間相當長,并且在測試完畢以后電池里面的電量全部放掉,因此這個方法只在實驗室中用來標定驗證電池的標稱容量,無法用于設計 BMS做車輛電池電量的在線估計。
2)安時積分法
安時積分計算方法為:
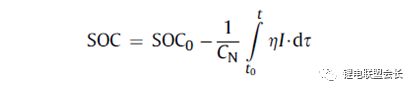
式中,SOC 為荷電狀態;SOC0為起始時刻(t0)的荷電狀態;CN為額定容量(為電池當時標準狀態下的容量,隨壽命變化);η為庫侖效率,放電為1,充電小于1;I 為電流,充電為負,放電為正。
在起始荷電狀態SOC0比較準確情況下,安時積分法在一段時間內具有相當好的精度(主要與電流傳感器采樣精度、采樣頻率有關)。但是,安時積分法的主要缺點為:起始SOC0影響荷電狀態的估計精度;庫侖效率η受電池的工作狀態影響大(如荷電狀態、溫度、電流大小等),η難于準確測量,會對荷電狀態誤差有累積效應;電流傳感器精度,特別是偏差會導致累計效應,影響荷電狀態的精度。因此,單純采用安時積分法很難滿足荷電狀態估計的精度要求。
3)開路電壓(OCV)法
鋰離子電池的荷電狀態與鋰離子在活性材料中的嵌入量有關,與靜態熱力學有關,因此充分靜置后的開路電壓可以認為達到平衡電動勢,OCV 與荷電狀態具有一一對應的關系,是估計荷電狀態的有效方法。但是有些種類電池的OCV 與充放電過程(歷史)有關,如LiFePO4/C電池,充電OCV與放電OCV 具有滯回現象(與鎳氫電池類似),并且電壓曲線平坦,因而SOC估計精度受到傳感器精度的影響嚴重,這些都需要進一步研究。開路電壓法最大的優點是荷電狀態估計精度高,但是它的顯著缺點是需要將電池長時靜置以達到平衡,電池從工作狀態恢復到平衡狀態一般需要一定時間,與荷電狀態、溫度等狀態有關,低溫下需要數小時以上,所以該方法單獨使用只適于電動汽車駐車狀態,不適合動態估計。
4)基于電池模型的開路電壓法
通過電池模型可以估計電池的開路電壓,再根據OCV 與SOC 的對應關系可以估計當前電池的SOC。等效電路模型是最常用的電池模型。
對于這種方法,電池模型的精度和復雜性非常重要。華等人收集了12個常用等效電路模型,包括組合模型,Rint模型(簡單模型),具有零狀態滯后模型的Rint模型,具有單態滯后模型的Rint模型,具有兩個低通濾波器增強型自校正(ESC)模型,具有四個低通濾波器的ESC模型,一階RC模型,一個狀態滯后的一階RC模型,二階RC模型,具有單態滯后的二階RC模型,三階RC模型和具有單態滯后的三階RC模型。
電化學模型是建立在傳質、化學熱力學、動力學基礎上,涉及電池內部材料的參數較多,而且很難準確獲得,模型運算量大,一般用于電池的性能分析與設計。
如果電池模型參數已知,則很容易找到電池OCV。然后使用通過實驗得出的OCV-SOC查找表,可以容易地找到電池SOC。研究人員使用這種方法,并分別采取RINT模型,一階RC,二階RC模型,發現使用二階RC模型的最大估計誤差是4.3%,而平均誤差是1.4%。
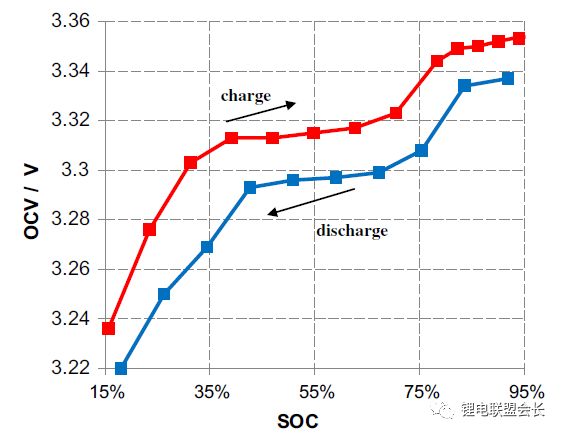
圖6充放電C /的LiFePO的OCV曲線4(在25℃測量,休息時間3小時)
5)神經網絡模型方法
神經網絡模型法估計SOC 是利用神經網絡的非線性映射特性,在建立模型時不用具體考慮電池的細節問題,方法具有普適性,適用于各種電池的SOC估計,但是需要大量樣本數據對網絡進行訓練,且估算誤差受訓練數據和訓練方法的影響很大,且神經網絡法運算量大,需要強大的運算芯片(如DSP等)。
6)模糊邏輯方法
模糊邏輯法基本思路就是根據大量試驗曲線、經驗及可靠的模糊邏輯理論依據,用模糊邏輯模擬人的模糊思維,最終實現SOC預測,但該算法首先需要對電池本身有足夠多的了解,計算量也較大。
7)基于電池性能的SOC 估計法
基于電池性能的SOC估計方法包括交流阻抗法、直流內阻法和放電試驗法。交流阻抗法是通過對交流阻抗譜與SOC 的關系進行SOC 估計。直流內阻法通過直流內阻與電池SOC 的關系進行估計。
交流阻抗及直流內阻一般僅用于電池離線診斷,很難直接應用在車用SOC實時估計中,這是因為,采用交流阻抗的方法需要有信號發生器,會增加成本;電池阻抗譜或內阻與SOC 關系復雜,影響因素多(包括內阻一致性);電池內阻很小,車用電池在毫歐級,很難準確獲得;鋰離子電池內阻在很寬范圍內變化較小,很難識別。
8)融合算法
目前融合算法包括簡單修正、加權、卡爾曼濾波或擴展卡爾曼濾波(EKF)、滑模變結構等。簡單修正的融合算法主要包括開路電壓修正、滿電修正的安時積分法等。
對于純電動車電池,工況較為簡單,車輛運行時除了少量制動回饋充電外主要處于放電態,站上充電時電池處于充電態,開路電壓的滯回效應比較容易估計;電池容量大,安時積分的誤差相對較小;充滿電的機率大,因此,采用開路電壓標定初值和滿電修正的安時積分方法可以滿足純電動車電池SOC 的估計精度要求。
對于混合動力車電池,由于工況復雜,運行中為了維持電量不變,電流有充有放;停車時除了維護外,沒有站上充電的機會;電池容量較小,安時積分的相對誤差大。因此,簡單的開路電壓修正方法還不能滿足混合動力車電池SOC 的估計精度要求,需要其他融合方法解決。
加權融合算法是將不同方法得到的SOC 按一定權值進行加權估計的方法。Mark Verbrugge等采用安時積分獲得SOCc與采用具有滯回的一階RC模型獲得SOCv的加權方法估計SOC,計算公式為
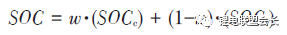
式中,w 為權值。該算法已經在GM混合動力系統中應用。
卡爾曼濾波是一種常用的融合算法。由于SOC不能直接測量,目前一般將兩種估計SOC 的方法融合起來估計。SOC被當成電池系統的一個內部狀態分析。又由于電池系統為非線性系統,因此采用擴展的卡爾曼濾波方法,通常采用安時積分與電池模型組成系統進行計算。Plett等研究了安時積分與組合模型、Rint模型(簡單模型)、零狀態滯回Rint模型、一狀態滯回Rint模型、加強自修正模型的卡爾曼濾波融合算法。Wang等研究了安時積分與二階RC模型的卡爾曼濾波融合算法。
夏超英等研究了安時積分與一階RC模型的卡爾曼濾波算法,指出EKF作為一個狀態觀測器,其意義在于用安時積分法計算SOC的同時,估計出電容上的電壓,從而得到電池端電壓的估計值作為校正SOC 的依據,同時考慮噪聲及誤差的大小,確定每一步的濾波增益,得到開路電壓法在計算SOC 時應占的權重,從而得到SOC 的最優估計。這樣就把安時積分法和開路電壓有機地結合起來,用開路電壓克服了安時積分法有累積誤差的缺點,實現了SOC 的閉環估計。同時,由于在計算過程中考慮了噪聲的影響,所以算法對噪聲有很強的抑制作用。這是當前應用最廣的SOC估計方法。
Charkhgard等采用卡爾曼濾波融合了安時積分與神經網絡模型,卡爾曼濾波用于SOC 計算的核心是建立合理的電池等效模型,建立一組狀態方程,因此算法對電池模型依賴性較強,要獲得準確的SOC,需要建立較為準確的電池模型,為了節省計算量,模型還不能太復雜。Ouyang等提出一種實時性好的基于電化學機理的等效電路模型的SOC 卡爾曼濾波算法,在保證計算速度基礎上,提高了SOC 的估計效果,尤其是低SOC 區的估計精度。但是卡爾曼濾波法的缺點還有卡爾曼增益不好確定,如果選擇不好狀態將發散。Kim等提出采用滑模技術克服卡爾曼濾波的缺點,據稱該方法對于模型參數不確定和干擾具有較強的魯棒性。
9)電池組SOC 估計
電池組由多節電池串并聯組成,由于電池單體間存在不一致性,成組后的電池組SOC 計算更為復雜。由多個電芯并聯連接的電池模塊可以被認為是具有高容量的單個電池,并且由于并聯連接的自平衡特性,可以像單個電池一樣估計SOC。
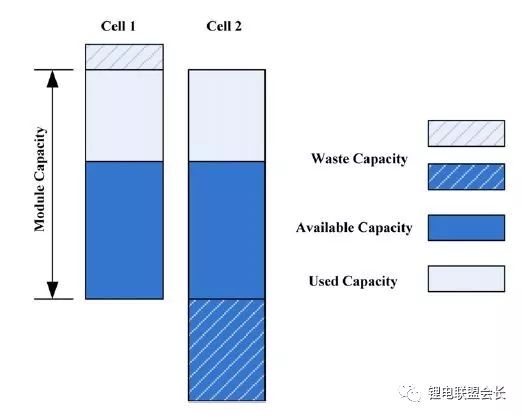
圖7 電池模塊的無用容量和剩余容量(以2個電池的電池模塊為例)
在串聯連接條件下,粗略的估計電池模塊的SOC也可以像單體電池一樣,但考慮到電池的均勻性,情形會有些不同。假設電池模塊中每個單體電池的容量和SOC是已知的。如果有一個非常高效且無損的能量均衡裝置,則電池模塊的SOC:
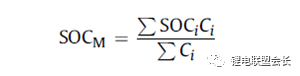
其中,SOCM表示電池模塊的SOC,SOCi表示第i個電池單元的SOC,Ci表示第i個電池單體的容量。如果平衡裝置不是那么有效,真正的電池模塊的SOC與該平衡裝置的實際性能有關。如果只有耗散式的被動均衡功能或者沒有均衡功能,則電芯中存在一部分無法利用的容量如圖6所示,并且隨著電池差異性的加劇,這種浪費的容量的比例會越來越大。因此,電池模塊的容量表示為:
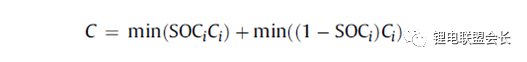
電池模塊可用容量表示為:

電池模組的荷電狀態表示為:
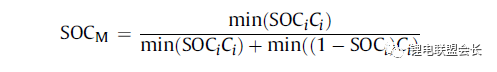
由此,在每一節電池單體SOC 都可估計的前提下,就可以得到電池組的SOC 值。要獲取單體的SOC值,最直接的方法就是應用上述SOC 估計方法中的一種,分別估計每一個單體的SOC,但這種方法的計算量太大。為了減小計算量,部分文獻[43~45]在估計電池成組的SOC 方法上做了一些改進研究。Dai 等[44]采用一個EKF 估計電池組平均SOC,用另一個EKF 估計每個單體SOC 與平均SOC 之差ΔSOC。估計ΔSOC 的EKF中需要估計的狀態量只有一個,因此算法的計算量較小。另外,考慮到ΔSOC 的變化很慢,采用雙時間尺度的方法可以進一步減小計算量。Zheng等提出了一種M+D模型,即一個相對復雜的電池單體平均模型M,和一個簡單的單體差異模型D,利用最小二乘法計算單體與“平均單體”之間的差值ΔOCV,通過ΔSOC 與ΔOCV 的關系,可以計算每個單體的SOC 值。
表2 各種SOC估計方法比較
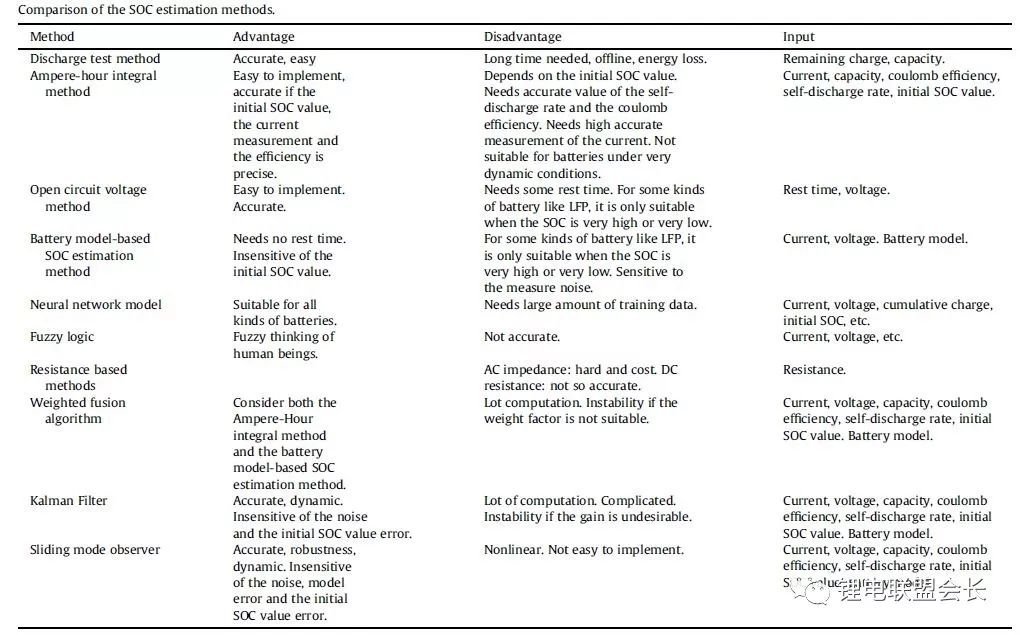
表3不同SOC估計方法的SOC估計誤差。
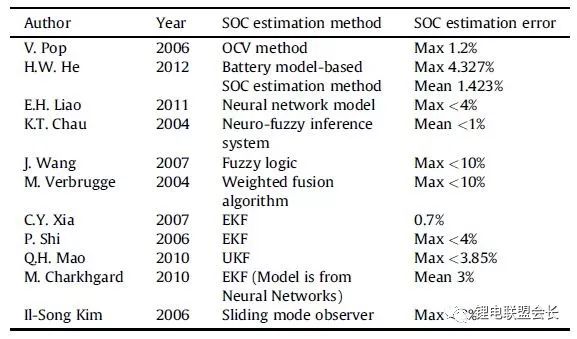
表2中比較了不同的SOC估算算法。表3總結了每種方法的SOC估計誤差。
綜合比較上述常用的SOC 估計方法,卡爾曼濾波等基于電池模型的SOC 估計方法精確可靠,配合開路電壓駐車修正是目前的主流方法。
參考文獻


下 篇
上篇和中篇兩篇文章中,介紹的BMS功能需求包括電池電壓測量、數據采樣頻率同步性,溫度估計和SOC估計。本文,是《一個典型的動力電池管理系統,需要實現哪些功能》的最后一個部分,內涉及SOH(健康狀態)估計、SOF(功能狀態)估計 及SOE(可用能量狀態)估計、SOS(安全狀態)估計。
3.3 健康狀態(SOH)估計
健康狀態是指電池當前的性能與正常設計指標的偏離程度。電池老化是電池正常的性能衰減,不能完全代表其健康狀態。而目前多數SOH的定義僅限于電池老化的范疇,沒有真正涉及電池的健康狀況(如健康、亞健康、輕微問題、嚴重問題等),因此目前的算法應該稱為壽命狀態。
耐久性是當前業界研究熱點,表征電池壽命的主要參數是容量和內阻。一般地,能量型電池的性能衰減用容量衰減表征,功率型電池性能衰減用電阻變化表征。為了估計電池的衰減性能,首先要了解電池的衰減機理。
鋰電池衰減機理。鋰離子電池為“搖椅式”電池,正負極的活性材料可以看作容納鋰離子的兩個水桶,鋰離子相當于桶里的水。電池的性能衰減可以理解為“水”變少(即活性鋰離子損失),或“桶”變小(正極或負極活性物質變少),如下圖所示。導致活性鋰離子損失的主要原因是:電極與電解液副反應形成鈍化膜(如SEI膜);由于充放電電池膨脹收縮疲勞導致電極龜裂,導致電極與電解液副反應形成新的SEI膜,消耗鋰離子;不當充電導致的析鋰與電解液反應消耗鋰離子。導致活性材料損失的主要原因包括:材料中的錳、鐵或鎳等離子溶解;活性材料顆粒脫落;活性材料晶格塌陷。目前SOH估計方法主要分為耐久性經驗模型估計法和基于電池模型的參數辨識方法。
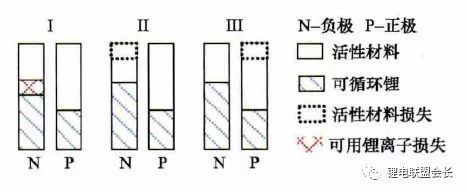
鋰離子電池雙水箱模型
1)耐久性經驗模型估計法
耐久性經驗模型估計法是基于電池耐久性測試數據標定獲得的模型,直接預測容量衰減和內阻的變化。電池的耐久性模型可以分為耐久性機理模型和耐久性外特性模型,兩者的主要區別在于,前者側重于對電池內部副反應機理的研究,并以SEI膜內阻、離子濃度等微觀量為觀測對象;而后者從試驗規律出發,重點關注電池循環過程中表現出來的容量衰減與內阻增加。有文獻根據正負極衰老機理,基于循環鋰離子損失機理以及電池內部的材料腐蝕機理,建立了電池SEI膜內阻增加模型以及循環衰減后的端電壓模型。由于詳細的鋰離子電池衰減機理十分復雜,目前還很難準確確定模型的參數,同時運算量也較大,一般不用于車用電池管理中。
基于電池外特性的模型,已經有較多文獻涉及,最常見的性能衰減模型是基于Arrhenius規律的模型。Toshiba的手冊中給出了鈷酸鋰電池貯存壽命模型
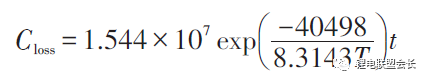
式中,Closs為容量損失百分比,%;T為溫度,K;t為時間,月。Bloom等進行了不同環境溫度下電池衰減率的試驗與分析,試驗了以溫度為加速應力的電池容量衰減模型,討論了電池容量保持率與環境溫度和循環時間的關系,提出
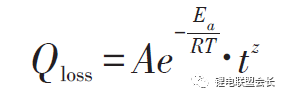
式中,Qloss 為阻抗增加率(area specific impedance ,ASI)或最大輸出功率,W/s或W;A為常數;Ea為反應活化能,J;R是氣體常量,J/(mol·K);T是絕對溫度,K;t是時間,h;z是時間模態,簡單情況下可取1/2。其中A、Ea/R、z都可以通過試驗數據用擬合的方法得到。
Wang等基于Bloom等的工作,提出了以Ah循環總量為變量的雙因素模型,將放電倍率乘入原有的時間項,得到以溫度和放電倍率為加速應力的電池壽命模型,實現了雙應力加速下20%以內的預測誤差,即
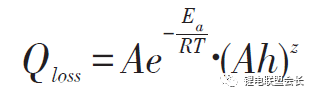
式中,Qloss為容量損失百分比,%;Ah為安時循環總量,Ah;其他參數的定義與前面公式相同。
Matsushima研究了大型鋰離子電池的性能衰減,發現容量的衰減與時間呈1/2次方關系,即Qloss=Kf×t^(1/2),并發現容量衰減在30%以內時的系數Kf與容量衰減大于30%時的系數Kf不相同。前者較大,說明前30%容量衰減的速度快。Kf服從阿倫尼烏斯定律。進一步地,基于Arrhenius模型的擴展模型,如黎火林、蘇金然根據對鈷酸鋰電池循環壽命的試驗,提出了如下的Arrhenius擴展模型:
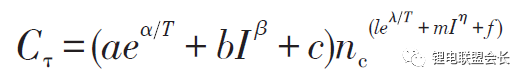
式中,Cτ為容量衰減率,%;nc為充放電循環壽命,次;T為絕對溫度,K;I為放電電流,A;a、b、c、l、m、f、α、β、λ、η均為常數,可以通過試驗擬合確定。
Li等考慮了電池壽命的多個影響因素,如環境溫度、放電倍率、放電截止電壓、充電倍率和充電截止電壓等,提出了基于耦合強度判斷和多因素輸入的壽命建模方法(模型中溫度的影響也參考了Arrhenius建模方法、電物理量的影響參考逆冪規律),并基于模型的因素敏感性分析了各因素對電池壽命影響的權重,耐久性模型對電池壽命的預測誤差為15%以內。
Han等在分析電池性能衰減基礎上,認為以石墨為負極的鋰離子電池的性能衰減主要是因為負極SEI膜增厚消耗活性鋰離子,正常的SEI膜增厚消耗的鋰離子與時間呈1/2次方關系,但一般電池存在疲勞龜裂消耗了更多的活性鋰離子,因此性能衰減與時間的關系大于1/2 次方。基于Arrhenius模型建立了4款以石墨為負極的鋰離子電池的性能衰減離散模型,并提出基于該離散模型的閉環參數修正方法,經過幾次容量修正后,模型參數趨于穩定。
其他外特性建模方法還有神經網絡模型,如Jungst等在研究以LiNi0.8Co0.15Al0.05O2為正極材料的電池貯存壽命時建立的神經網絡模型。借鑒機械疲勞研究成果,Safari等采用機械疲勞研究中常用的Palmgren-Miner(PM)法則預測電池容量在簡單和復雜工況下的衰減情況,并與損害時間累計法(capacity-lossaccumulation over time,LAT)進行比較,結果表明PM法好于LAT法。
2)基于電池模型參數辨識法
參數辨識方法主要基于已有的電池模型,采用最優狀態估計技術,如最小二乘法、卡爾曼濾波等算法,根據運行的數據,對電池模型參數如容量、內阻等進行辨識,從而獲得電池的壽命狀態。
Plett將內阻和容量作為系統狀態參數,構建了內阻估計狀態方程和容量估計狀態方程。采用擴展的雙卡爾曼濾波方法獲得內阻和容量。Gould也基于卡爾曼濾波方法和線性擬合方法辨識電池模型中的容量,繼而獲得容量隨運行循環數的衰減情況。還有將電池等效電路模型中的內阻視為低頻阻抗,采用滑模控制技術進行辨識。Remmlinger介紹了一種用于混合動力車的電池內阻在線辨識方法,為了實現在線應用,改進了二階RC模型,然后基于特殊的負載信號(發動機啟動時的短暫電壓及電流),采用線性最小二乘法獲得電池模型的內阻值。Verbrugge認為如果對系統狀態參數、測量參數和噪音的演變過程比較了解,采用卡爾曼濾波優化算法來遞歸辨識是最具有代表性的方法。如果缺乏對狀態參數、測量參數、噪音的全面了解,采用具有時間指數遺忘因子的加權遞推最小二乘法將是一個較為務實的方法。Wang發現Verbrugge采用疊加積分計算電壓的電池模型遞推算法在采樣頻率較高時變得不是很穩定。據此改進了電池模型的算法,并同樣也采用指數遺忘因子的加權遞推最小二乘法辨識電池參數(開路電壓及內阻等)。Chiang采用線性或非線性系統控制中常用的自適應控制方法,建立了基于電池等效電路模型的參數估計框架,其中為了便于采用自適應控制技術,鋰離子電池等效電路模型采用狀態方程來描述,可用于在線監測電池內阻及OCV,分別用于確定SOH和SOC。Einhorn根據ΔSOC=ΔAh/C的關系,估計容量的大小,方法為:
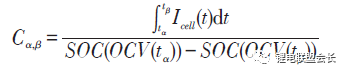
式中,任意兩個時刻(α ,β)的SOC由OCV查表得到,該方法可在實際中應用,可以取若干個點,兩兩搭配計算出多個容量值,再取平均值或中位數。這種方法比較簡單,但關鍵在于OCV能否精確辨識。
3)電池組SOH估計
在不進行均衡的條件下,電池組的容量衰減將遠大于單體的容量衰減,鄭岳久等提出用兩維散點圖解釋電池組容量衰減的機理,指出電池組的容量衰減量為剩余充電電量最小單體的容量損失與單體間負極的活性鋰離子損失差異之和。為了得到電池組的容量,需要首先獲得單體的容量。單體容量獲取可以通過上述基于模型參數的辨識方法獲得,也可以通過充電電壓曲線變換方法獲取。
3.4 功能狀態(SOF)估計
估計電池SOF可以簡單認為是在估計電池的最大可用功率。一般而言,電池的最大可用功率受到電流、電壓、SOC、溫度等參數的限制,還與電池的老化程度、故障狀態等有關。常用的SOF估計方法可以分為基于電池MAP圖的方法和基于電池模型的動態方法兩大類。
1)基于MAP圖算法
基于電池測試(通常為HPPC測試)數據和最大、最小電壓限制,可以獲得在不同SOC下的最大充放電功率。在不同溫度、不同衰減程度下進行電池測試,可以建立最大充放電功率與溫度、SOC、SOH的關系,得到最大充放電功率MAP圖。基于MAP圖,實車BMS可以通過插值得到電池的最大充放電功率,實現SOF估計。
Do等分別研究了不同SOC、溫度、累計放電容量下的最大充放電功率,并建立了最大充放電功率的函數解析式,實現了對SOF的預測。基于MAP圖的估計方法簡單直接,但需要存儲多維MAP圖,并且只考慮了靜態特性,而對動態工況下的充放電功率估計有一定的局限性。
2)基于電池模型的動態算法
根據電池模型,綜合考慮電池的電流、電壓、SOC、功率等限制,可以得到最大充放電電流,從而計算得到電池的最大充放電功率。韓雪冰根據電池模型,給出不同電流輸入情況下電池的端電壓情況,通過迭代計算,獲得電池單體在電壓限制條件下所允許的最大電流Imax,voltage 和最小電流Imin,voltage,并且從電池的機理出發,考慮了電池副反應速率限制下的最大最小電流,其方法類似于求取端電壓限制下的最大充放電電流。最后綜合考慮上述限制,獲得電池單體的最大最小電流。Sun 等分析比較了幾種最大可用功率預測方法,包括HPPC法、SOC限制法、電壓限制法,以及基于動態模型的多參數估計法,并通過HPPC測試得到充放電電阻,基于Rint模型,利用端電壓限制,估計電池的最大充放電功率。但這種方法估計的實際上是瞬時最大功率。并且由于Rint模型不夠精確,可能過于樂觀地估計了功率,還可能引起過充過放。與前述方法基本相同,Sun等認為若允許的SOC變化范圍很大,計算出的最大最小電流可能很大,并不合理,應與其他方法聯合使用。電壓限制法考慮在端電壓限制下一段時間內的最大充放電功率,但仍使用了Rint模型,原理上與前述方法類似,只是算法上并沒有采用迭代估計的方法,而是基于模型直接計算電流限值。基于動態模型的多參數估計方法實質上是基于Thevenin模型的電壓限制法,綜合SOC與電流的限制,進而得到最大充放電電流。
以上是獲得電池單體最大充放電電流的方法。實車上電池組由眾多電池單體組成,由于單體之間存在不一致性,若要單獨計算每個電池單體的最大可用功率,計算量太大,
韓雪冰提出了充、放電關鍵電池單體的概念,以減少計算量。綜合考慮各種限制條件,可以得到最終的最大最小電流Imax,total和Imin,total,將Imax,total、Imin,total代入電池模型中可計算得到對應的端電壓Umax,total,Umin,total,進一步可以得到最大充放電功率,即
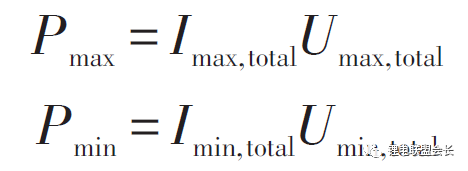
3.5 剩余能量(RE)或能量狀態(SOE)估計
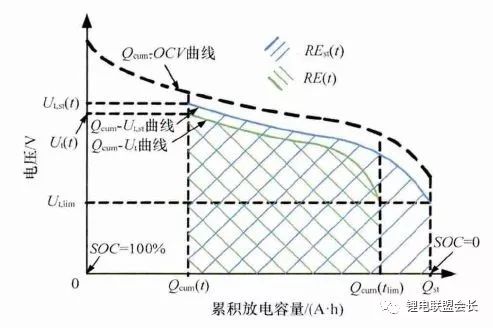
剩余能量(RE)或能量狀態(SOE)是電動汽車剩余里程估計的基礎,與百分數的SOE相比,RE在實際的車輛續駛里程估計中的應用更為直觀。在電動汽車使用過程中,電池的剩余能量(RE)是指以某一工況行駛時,從當前時刻直至電池放電截止過程中,電池累計提供的能量。RE可以由電池端電壓Ut與相應的累積放電容量Qcum組成的坐標系上的面積表示,如下圖所示。
電池剩余能量示意圖
當前時刻t的電池端電壓為Ut(t),放電截止時刻記為tlim,對應的端電壓為電池允許的最低放電電壓Ut(tlim)。當前時刻的荷電狀態為SOC(t),已累積的放電容量為Qcum(t)。放電截止時刻tlim 對應的SOC和累積容量分別記為SOClim和Qcum(tlim)。圖中,端電壓變化表示為綠色曲線,曲線下圍成的(綠色斜線)面積對應電池當前時刻在此種工況下的剩余能量RE(t),其計算過程對應公式如下。
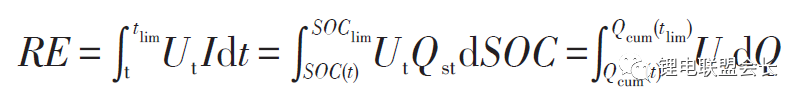
由于不同的充放電情況對應的端電壓響應不同,使得電池在同一時刻t提供的剩余能量RE(t)也不相同。此處用一組標準電流倍率下的放電情況作對照,標準情況的端電壓Ut,st如圖中藍色曲線(Qcum-Ut,st)所示。由電池SOC和標準放電容量的定義,此時放電截止位置的SOC值SOClim,st為0,累積放電容量Qcum,st等于電池標準容量Qst。標準放電工況下對應的剩余能量REst(t)與之前的RE(t)有明顯的差距。電池剩余放電能量的差異同樣可以由當前的RE(t)與理論上最大的剩余放電能量(電池開路電壓OCV曲線圍成的面積,圖中黑色虛線所示)進行比較。
不同放電工況下電池的能量損失不同,因此只有預測某一特定功率需求下的電池電壓響應過程,才能獲得準確的RE預測值。由于鋰離子電池的特點,其電壓輸出受到很多變量的影響,如當前SOC、溫度、衰減程度SOH,因此在能量預測過程中除傳統的SOC估計模型外,還需要一個專門的電壓預測模型。劉光明等提出一種適用于動態工況的電池剩余放電能量精確預測方法EPM(energy prediction method),如下圖所示,該方法基于當前的電池狀態和未來的電流輸入,根據電池模型對未來放電過程的電壓變化進行預測,并計算放電過程中的累積能量。預測過程中,根據當前的電壓、電流測量值對模型參數進行修正,對端電壓序列與RE的預測結果進行更新。
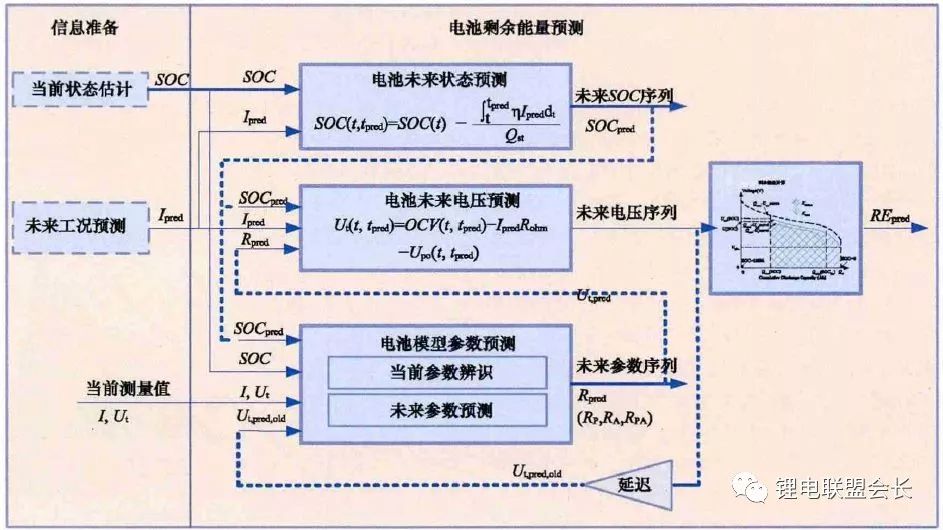
電池剩余放電能量預測方法(EPM)結構
3.6 故障診斷及安全狀態(SOS)估計
故障診斷是保證電池安全的必要技術之一。安全狀態估計屬于電池故障診斷的重要項目之一,BMS可以根據電池的安全狀態給出電池的故障等級。目前導致電池嚴重事故的是電池的熱失控,以熱失控為核心的安全狀態估計是最迫切的需求。導致熱失控的主要誘因有過熱、過充電、自引發內短路等。研究過熱、內短路的熱失控機理可以獲得電池的熱失控邊界。Feng等研究了一款三元電池的熱失控行為,獲得了3個特征溫度。Ouyang等研究了一款復合三元材料電池的過充電熱失控行為,獲得了4個過充電特征階段。這些研究為電池的安全狀態估計提供了基礎。
故障診斷技術目前已發展成為一門新型交叉學科。故障診斷技術基于對象工作原理,綜合計算機網絡、數據庫、控制理論、人工智能等技術,在許多領域中的應用已經較為成熟。鋰離子電池的故障診斷技術尚屬于發展階段,研究主要依賴于參數估計、狀態估計及基于經驗等方法(與上述SOH研究類似)。Bohlen等通過電池內阻模型的在線辨識實現了電池在線診斷。Sun等鉛酸電池的健康狀態(SOH)上,假設正常狀態的恒流充放電電壓曲線是光滑的,通過觀察其充放電曲線的變化辨識電池組可能存在的故障。電動汽車動力往往由成百上千個電池單體串并聯構成,個體之間存在一定的差異,即不一致性。一般地,不一致性服從統計分布規律,這為電池組的故障診斷提供了一種理論依據。
Zheng等建立了一種考慮接觸電阻的電池分頻模型,以代表低頻的電池平均模型研究電池組總體行為,以代表高頻的差異模型研究電池組一致性問題,成功辨識了電池組內的接觸電阻故障。Ouyang等同樣采用分頻模型,通過內短路電池造成一致性變差特性來診斷內短路的發生。
參考文獻



-
電動汽車
+關注
關注
156文章
12158瀏覽量
231959 -
動力電池
+關注
關注
113文章
4546瀏覽量
77816 -
電池管理
+關注
關注
27文章
554瀏覽量
43027
原文標題:一個典型的動力電池管理系統,需要實現哪些功能(完全篇)
文章出處:【微信號:Recycle-Li-Battery,微信公眾號:鋰電聯盟會長】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 一個典型的動力電池管理系統具體都需要關注哪些功能呢?
一個典型的動力電池管理系統具體都需要關注哪些功能呢?











評論