1. 設計電壓

電纜及附件的設計必須滿足額定電壓、雷電沖擊電壓、操作沖擊電壓和系統最高電壓的要求。其定義如下：

額定電壓

額定電壓是電纜及附件設計和電性試驗用的基準電壓，用U0/U表示。

U0——電纜及附件設計的導體和絕緣屏蔽之間的額定工頻電壓有效值，單位為kV；

U——電纜及附件設計的各相導體間的額定工頻電

壓有效值，單位為kV。

雷電沖擊電壓

UP——電纜及附件設計所需承受的雷電沖擊電壓的峰值，既基本絕緣水平BIL，單位為kV。

操作沖擊電壓

US——電纜及附件設計所需承受的操作沖擊電壓的峰值，單位為kV。

系統最高電壓

Um——是在正常運行條件下任何時候和電網上任何點最高相間電壓的有效值。它不包括由于故障條件和大負荷的突然切斷而造成的電壓暫時的變化，單位為kV。

定額電壓參數見下表（點擊放大）

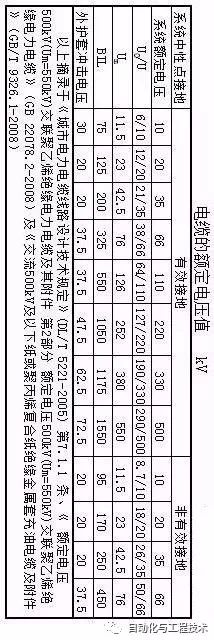
330kV操作沖擊電壓的峰值為950kV；500kV操作沖擊電壓的峰值為1175kV。

2. 導體電阻

2.1導體直流電阻

單位長度電纜的導直流電阻用下式計算:

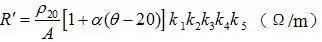
20℃導體直流電阻詳見下表（點擊放大）：

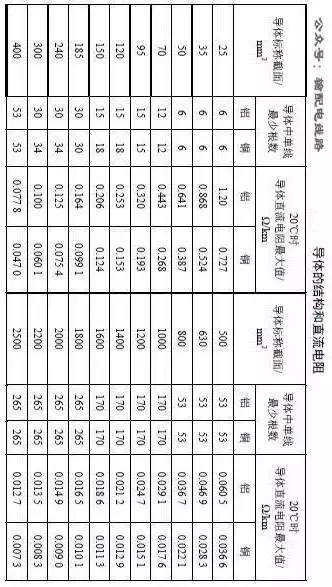
以上摘錄于《10(6)kV～500kV電纜技術標準》（Q∕GDW 371-2009 ）。

2.2導體的交流電阻

在交流電壓下，線芯電阻將由于集膚效應、鄰近效應而增大，這種情況下的電阻稱為有效電阻或交流電阻。

電纜線芯的有效電阻，國內一般均采用IEC-287推薦的公式:

R=R′(1+YS+YP)

式中：

R——最高工作溫度下交流有效電阻，Ω/m；

R′——最高工作溫度下直流電阻，Ω/m；

YS——集膚效應系數，YS=XS4/(192+0.8XS4)，

XS4=（8πf/R′×10-7kS）2；

YP——鄰近效應系數，YP=XP4/(192+0.8XP4)(Dc/S)2{0.312(Dc/S)2+1.18/[XP4/(192+0.8XP4)+0.27]}，XP4=（8πf/R′×10-7kP）2。

XS4——集膚效應中頻率與導體結構影響作用；

XP4——鄰近效應中導體相互間產生的交變磁場影響作用；

f——頻率；

Dc——線芯直徑，m；

S——線芯中心軸間距離，m；

ks——線芯結構常數，分割導體ks=0.435，其他導體ks=1.0；

kp——線芯結構系數，分割導體kp=0.37，其他導體kp=

0.8~1.0；

對于使用磁性材料制做的鎧裝或護套電纜，Yp和Ys應比計算值大70%，即:

R=R′[1+1.17(YS+YP)]

3. 電纜的電感

3.1自感

則單位長度線芯自感：

Li=2W/(I2L)=μ0/(8π) =0.5×10-7

式中：

Li——單位長度自感，H/m；

μ0——真空磁導率，μ0=4π×10-7，H/m；

以上一般是實心圓導體，多根單線規則扭絞導體如下表：

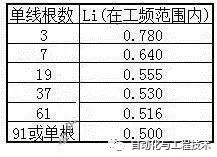
因誤差不大，計算一般取Li=0.5×10-7H/m。

3.2高壓及單芯敷設電纜電感

對于高壓電纜，一般為單芯電纜，若敷設在同一平面內（A、B、C三相從左至右排列，B相居中，線芯中心距為S），三相電路所形成的電感根據電磁理論計算如下：

對于中間B相：

LB=Li+2ln(2S/Dc) ×10-7(H/m)

對于A相：

LA=Li+2ln(2S/Dc) ×10-7 -α(2ln2 )×10-7(H/m)

對于C相：

LC=Li+2ln(2S/Dc)×10-7-α2(2ln2)×10-7(H/m)

式中：

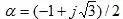
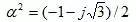
實際計算中，可近似按下式計算：

LA=LB=LC=Li+2ln(2S/Dc) ×10-7 ( H/m)

同時，經過交叉換位后，可采用三段電纜電感的平均值，即：

L=Li+2ln(2×(S1S2S3)1/3/Dc)×10-7(H/m)

=Li+2ln(2×21/3S/Dc) ×10-7 ( H/m)

對于多根電纜并列敷設，如果兩電纜間距大于相間距離時，可以忽略兩電纜相互影響。

3.3三相電纜的電感

主要計算中低壓三相電纜三芯排列為“品”字形電纜。根據電磁場理論，三芯電纜工作電感為：

L=Li+2ln(2S/Dc) ×10-7

式中：

L——單位長度電感，H/m；

S——電纜中心間的距離，m；

若三芯電纜電纜中心間的距離不等距，或單芯三根品字排列時三相回路電纜的電感按下式計算：

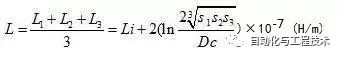
式中：

S1、S2、S3——電纜各相中心之間的距離，m。

4. 電纜金屬護套的電感

4.1三角排列

三根單芯電纜按等邊三角形敷設的三相平衡負載交流回路，護套開路，每相單位長度電纜金屬護套的電感為：

Ls=2ln(S/rs)×10-7(H/m)

式中：

rs——電纜金屬護套的平均半徑，m。

4.2等距直線排列

三根單芯電纜按等距離平面敷設的三相平衡負載交流回路，護套開路，每相單位長度電纜金屬護套的電感為：

對于中間B相：

LSB=2ln(S/rs)×10-7(H/m)

對于A相：

LSA=2ln(S/rs)×10-7-α(2ln2)×10-7(H/m)

對于C相：

LSC=2ln(S/rs)×10-7-α2(2ln2)×10-7(H/m)

式中：

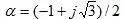
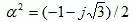
三相平均值：

LS=2ln(S/rs)×10-7+2/3?ln2×10-7(H/m)

4.3任意直線排列

三根單芯電纜平面敷設的三相平衡負載交流回路，電纜換位，護套開路，每相單位長度電纜技術護套的電感為：

LSB=2ln(((S1S2S3)1/3)1/3/rs)×10-7(H/m)

5. 電纜電抗、阻抗及電壓降

5.1電抗

電纜的電抗為：

X=ωL(Ω/m)

式中：

L——電纜單位長度的電感，H/m;

ω=2πf。

5.2阻抗

電纜的阻抗為：

Z=（R2+X2）1/2(Ω/m)

式中：

R——電纜單位長度的交流有效電阻，Ω/m。

5.3電壓降

電纜的電壓降為：

△U=IZl (V)

式中：

I——導體電流，A；

l——電纜長度，m。

6. 電纜的電容

7. 計算實例

一條電纜型號YJLW02-64/110-1X630長度為2300m,導體外徑Dc=30mm，絕緣外徑Di=65mm，電纜金屬護套的平均半徑rs=43.85，線芯在20°C時導體電阻率ρ20=0.017241×10-6Ω·m ，線芯電阻溫度系數α=0.00393℃-1 ，k1k2k3k4k5≈1，電纜間距100mm，真空介電常數ε0=8.86×10-12 F/m，絕緣介質相對介電常數ε=2.5,正常運行時載流量420A。計算該電纜的直流電阻，交流電阻、電感、阻抗、電壓降及電容。

計算如下：

1.直流電阻

根據直流電阻公式：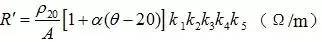

得：

R＇=0.017241×10-6(1+0.00393(90-20))/(630×10-6)

= 0.3489×10-4（Ω/m）

該電纜總電阻為R=0.3489×10-4×2300 = 0.08025（Ω）

2.交流電阻

由公式YS=XS4/(192+0.8XS4)，XS4=（8πf/R′×10-7kS）2得：

XS4=(8×3.14×50/0.3489×10-4)×10-14= 12.96

YS=12.96/( 192+0.8×12.96) = 0.064

由公式XP4=（8πf/R′×10-7kP）2得：

XP4=(8×3.14×50/0.3489×10-4)×10-14= 12.96

由公式YP=XP4/(192+0.8XP4)(Dc/S)2{0.312(Dc/S)2+1.18/[XP4/(192+0.8XP4)+0.27]}得：

YP=12.96/(192+0.8×12.96)(30/100)｛(0.312(30/100)+1.18/(12.96/(192+0.8×12.96)+0.27)｝= 0.02

有公式R=R′(1+YS+YP)得：

R=0.3489×10-4(1+0.064+0.02) =0.378×10-4(Ω/m)

該電纜交流電阻RZ=0.378×10-4×2300 = 0.8699 (Ω)

3.電感

由公式L=Li+2ln(2S/Dc) ×10-7得到單位長度電感：

L1=0.5×10-7+2ln(2×100/65)×10-7 =2.75×10-7（H/m）

該電纜總電感為L=2.75×10-7×2300=0.632×10-3H

4.金屬護套的電感

由公式LS=2ln(S/rs)×10-7+2/3?ln2×10-7得到單位長度金屬護套的電感：

LS1=2ln(100/43.85)×10-7+2/3?ln2×10-7

=2.11×10-7H/m

該電纜金屬護套的電感為LS=2.11×10-7H/m×2300=0.4855×10-3H

5.電抗、阻抗及電壓降

由公式X=ωL得到電抗：

X=2πf×0.632×10-3=0.199Ω

由公式Z=（R2+X2）1/2得到阻抗：

Z=（ 0.86992+0.1992）1/2=0.8924Ω

由公式△U=IZl 得到電壓降為：

△U=500×0.8924Ω=374.8V

6.電容

由公式C=2πε0ε/ln(Di/Dc)得到單位長度電容：

C1=2×3.14×8.86×10-12×2.5/Ln(65/30)= 0.179×10-6 F/m

該電纜總電容為C=0.179×10-6×2300 = 0.411×10-3 F