線彈性模型是結構力學分析中最基礎的材料模型。雖然聽上去微不足道,但模型中卻包含不少難以一眼看出的重要細節。在本篇文章中,我們將深入討論線彈性材料模型的相關理論和應用,并且大致介紹其各向同性和各向異性、材料數據的容許值、不可壓縮性,以及與幾何非線性之間的相互作用。
各向同性線彈性
在絕大多數涉及線彈性材料的仿真中,我們都要模擬完全不具有方向敏感性的各向同性材料。描述這種材料只需要兩個獨立材料參數。有很多方法來選擇合適的參數,不過其中某些參數則更為常用。
楊氏模量、剪切模量和泊松比
楊氏模量、剪切模量和泊松比是材料數據表中最常見的參數。它們不是獨立參數,因為剪切模量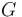
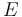
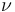
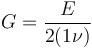
楊氏模量可以通過單軸拉伸試驗直接測量,而剪切模量可以通過純扭試驗測量。
在單軸試驗中,泊松比用于確定材料的橫向收縮(或拉升)程度。其容許范圍為 -1 <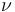
對于大部分金屬和合金而言,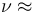
在給定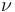
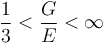
當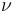
體積模量
體積模量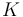
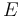

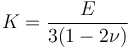
當

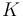
體積模量往往與剪切模量被一起指定。從某種意義上講,這兩個參數是最獨立的參數選擇。體積變化僅僅取決于體積模量,扭曲則完全受剪切模量決定。
拉梅常數
拉梅常數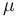

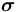
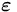
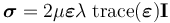
常數
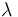
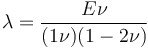
線彈性材料的不可壓縮性
橡膠一類的材料幾乎不可壓縮。從數學角度來說,完全不可壓縮材料與可壓縮材料具有本質的區別。因為不會發生體積變化,因此無法確定其平均應力。平均應力(壓力)p是體積變化
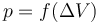
不成立,而必須用一個約束說明進行替代
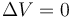
不可壓縮性還有另一個角度需要注意,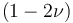
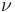
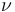
想法可行,但在這種情況中,基于標準位移的有限元公式可能得出不理想的結果,這是由鎖定現象引起的。造成的后果包括:
-
模型過于生硬。
-
應力呈棋盤式分布。
-
方程的病態導致求解器發生錯誤或發出警告。
補救方法是使用混合方程,將壓力作為額外自由度引入。在 COMSOL Multiphysics 中,勾選材料模型設置窗口中的幾乎不可壓縮材料復選框,即可啟用混合方程。
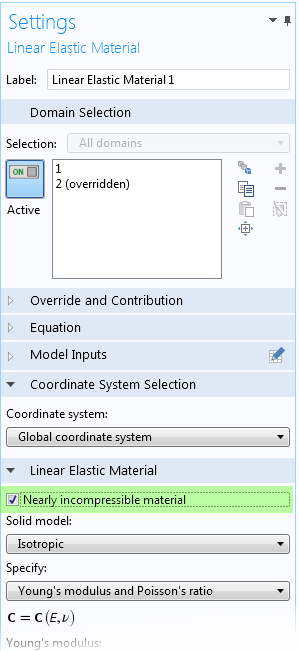
為線彈性材料啟用混合公式的部分設置。
當泊松比約大于或等于 0.45 時,體積模量比剪切模量大超過一個數量級,因此使用混合公式是明智的做法。其效果示例如下圖所示。
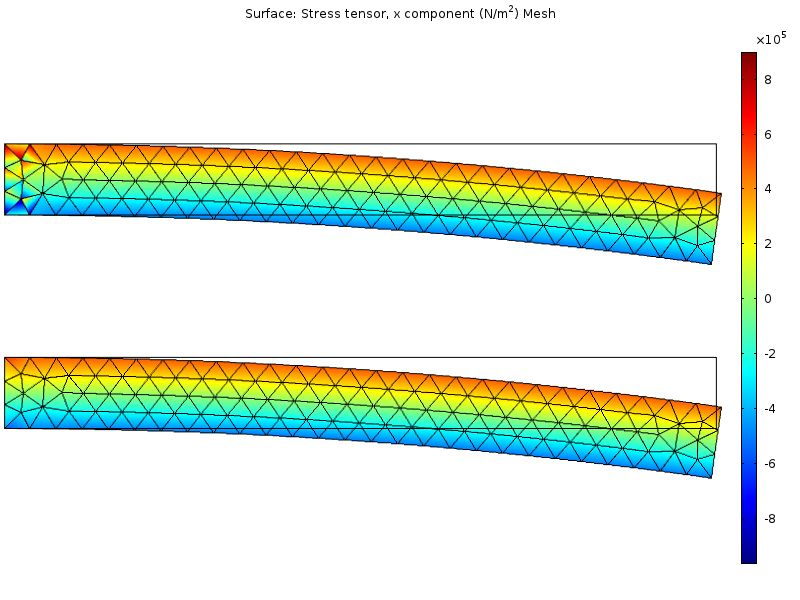
一個簡單的平面應變模型中的應力分布,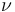 = 0.499。上方的圖表示基于標準位移的方程,下方的圖表示混合方程。
= 0.499。上方的圖表示基于標準位移的方程,下方的圖表示混合方程。
在僅涉及位移自由度的解中,其應力分布圖在左端(即存在約束的位置)呈現出扭曲的狀態。使用混合公式后,這些扭曲幾乎全部消失。
正交各向異性和各向異性
在一般情況下,線彈性材料的材料屬性都具有方向敏感性。其中最普遍的特性是各向異性,這意味著全部六個應力分量都取決于各自不同的應變分量。完整表示這些分量需要 21 個材料參數,很明顯,獲取全部數據是一項艱巨的任務。如果將應力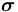
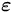
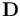
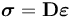
幸運的是,各向異性材料通常會表現一定的對稱性。在正交各向異性材料中,有三個正交方向上的剪切作用和軸向動作實現解耦。也就是說,當材料沿著其中一個主方向拉伸時,它只會在兩個正交方向上收縮,而不會受剪切力的作用。完整描述正交各向異性材料需要九個獨立材料參數。
當以柔度形式記錄時,正交各向異性材料的本構關系會更加清晰明了,其中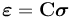
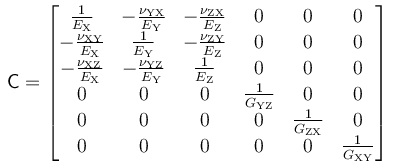
由于柔度矩陣必然是對稱的,因此使用的十二個常數可通過符合下方形式的三個對稱關系減少為九個
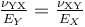
請注意
各向異性和正交各向異性常見于非均質材料。其材料屬性通常不是由測量得到的,人們更傾向于通過從微觀到宏觀尺度的均質化過程計算這些屬性。關于這種均質化作用在完全不同的研究背景中的討論,請訪問文末“閱讀原文”查看這篇文章。
對于非各向同性材料來說,使用描述各向同性材料的類似材料參數進行計算,在取值上可能會受到一些限制。我們雖難以立即發現這些限制,但有兩個注意事項會對我們找到限制有所幫助:
-
本構矩陣
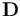
-
對于各向異性材料,唯一的選擇是檢查是否所有特征值都為正。
-
對于正交各向異性材料,適用條件為:全部六個彈性模量皆為正,且
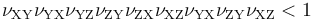
-
-
如果材料的壓縮率低,則必須使用混合方程。
-
我們可以估計等效體積模量和剪切模量的值。
-
在不確定的情況下,為了避免可能出現的誤差,最好在混合方程中引入額外自由度。
-
幾何非線性
在解決幾何非線性問題時,“線彈性”的含義實際上是一個常規問題。這里的問題是,我們有多種應力和應變的數學表示方式。如希望了解有關應力和應變的不同測量方式,請點擊文末的“閱讀原文”查看這一文章。
因為在 COMSOL Multiphysics 中,主應力和應變量分別為第二 Piola-Kirchhoff 應力和 Green-Lagrange 應變,因此線彈性自然地被解釋為兩個量之間的線性關系。人們有時將這種材料稱作 St. Venant 材料。
人們通常憑直覺認為“線彈性”指的是簡單拉伸試驗中力與位移的線性關系。事實并非如此,因為應力和應變都取決于變形。為了理解這一點,我們來看一看橫截面為正方形的條塊。
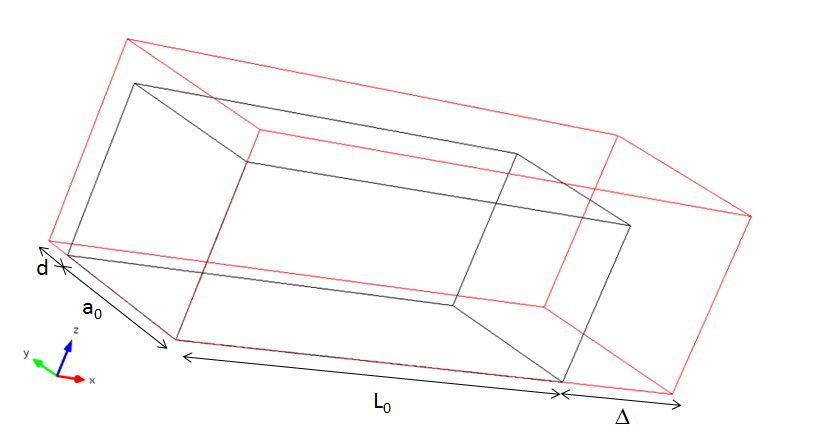 受到均勻拉伸的條塊。
受到均勻拉伸的條塊。
條塊的初始長度為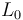
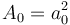
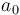

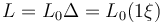
在這里,

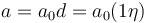
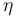
力可表示為軸向 Cauchy 應力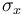

為了使用線彈性關系,Cauchy 應力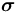
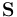
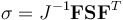
其中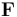
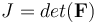

由于對受到單軸拉伸作用的 St. Venant 材料來說,其軸向應力與軸向應變的關系為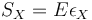
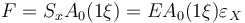
已知 Green-Lagrange 應變張量在軸向上的項定義為

所以力與位移的關系為
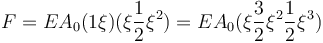
具有幾何非線性的線彈性材料實際上意味著力與工程應變(或者力與位移之間,因為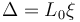

幾何非線性條件下的線彈性材料單軸響應。
如圖所示,受壓側的材料剛度接近于零:
-
通常,在引入更復雜的材料模型之前,您可能想快速檢查一遍“數量級”。
-
模型中存在奇異點,并且致使某一點上產生了極高的應變。
-
點擊此處,閱讀更多關于奇異點的知識。
-
-
接觸問題中的研究總是圍繞幾何非線性問題。
-
高壓縮應變通常在分析過程中出現于某一時刻的局部接觸區域。
-
對于以上所有情況來說,如果壓縮應力過大,求解器也許會無法求解。如果您懷疑我們的示例屬于這種情況,繪制最小主應變是一個很好的檢測方法。如果它小于 -0.3 左右,我們就預測到會發生類似故障。由 Green-Lagrange 應變得到的臨界值結果為 -1/3,如果這是一個問題,您應該考慮更換一個合適的超彈性材料模型。
壓縮或許不是唯一的問題。在上述分析里,泊松比沒有出現在方程中。那么橫截面的情況如何呢?
根據單軸情況中的定義,橫向應變與軸向應變的關系為
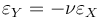
當這些應變是 Green-Lagrange 應變時,這便是一個非線性關系,可表述為
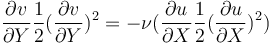
因此橫截面的變化具有很強的非線性。求解這個二次方程可得出如下的工程應變之間的關系
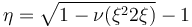
結果如下圖所示。
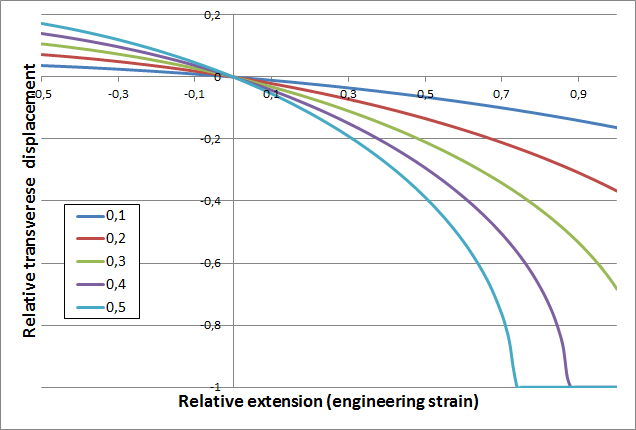
St. Venant 材料受到單軸拉伸作用時,其橫向位移隨軸向位移而變化。圖中顯示了五個不同的泊松比的值。
如您所見,當泊松比的值更高時,橫截面在大拉伸應力的作用下的塌陷更為迅速。
如果選擇另一種應力和應變數學表述方式,例如 Cauchy 應力與對數或“真實的”應變成正比,那么我們將得到完全不同的響應。當力-位移響應取決于泊松比的值時,這種材料的剛度反而會隨著拉伸而下降。雖然在兩個不同的仿真平臺中,利用大應變彈性計算出的結果存在巨大差異,但兩種材料仍舊皆可稱為“線彈性”材料。
-
模擬技術
+關注
關注
17文章
470瀏覽量
40383 -
半導體材料
+關注
關注
11文章
573瀏覽量
30174
原文標題:模擬線彈性材料能有多難?
文章出處:【微信號:COMSOL-China,微信公眾號:COMSOL】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
穩態太陽光模擬器 | 在航空航天材料測試中的應用

太陽模擬器技術新突破:鹵素-LED混合光源的大面積應用研究

功率半導體器件——理論及應用
射頻電路設計——理論與應用
【「基于大模型的RAG應用開發與優化」閱讀體驗】+Embedding技術解讀
【「基于大模型的RAG應用開發與優化」閱讀體驗】+大模型微調技術解讀
【「大模型啟示錄」閱讀體驗】對大模型更深入的認知
Samtec 技術簡報 | 探索非磁性互連























評論