一、時(shí)域和頻域

時(shí)域是瞬息萬(wàn)變的，頻域是亙古不變的。

傅里葉先是在他那個(gè)年代有了一個(gè)十分超前的想法，所有波都是不同的幅度、頻率、相位的正弦波組成的，這在當(dāng)時(shí)，包括他的老師都是持反對(duì)意見(jiàn)的，理由很簡(jiǎn)單，你拿線條圓滑的正弦給我組個(gè)線條筆直的方波、三角波看看。

然后傅里葉就整了一個(gè)傅里葉變換（以下簡(jiǎn)稱FT）出來(lái)，證明方波、三角波至少在數(shù)學(xué)上就是可以用正弦波組合出來(lái)，但是當(dāng)時(shí)沒(méi)有什么物理上的證明。

隨著歐洲工業(yè)革命的興起，特別是近幾十年來(lái)圖像處理技術(shù)的登峰造極，現(xiàn)在人們?cè)缫呀?jīng)不是去證明其真?zhèn)危墙柚@把工具來(lái)處理形形色色的應(yīng)用。這么說(shuō)吧，F(xiàn)T是處理“波”的，而“波”就是一種信號(hào)，所以只要涉及到信號(hào)這個(gè)層面的內(nèi)容，F(xiàn)T都可以發(fā)揮一定的作用。

FT的本質(zhì)，是時(shí)域的周期性連續(xù)信號(hào)可以在頻域上由不同頻率和幅度的正弦波的疊加，我們通過(guò)下面這張圖來(lái)說(shuō)明一下這個(gè)問(wèn)題。比如一個(gè)方波被不同數(shù)量、不同頻率和不同幅度多疊加后對(duì)比可以讓我們很初步的認(rèn)識(shí)FT。

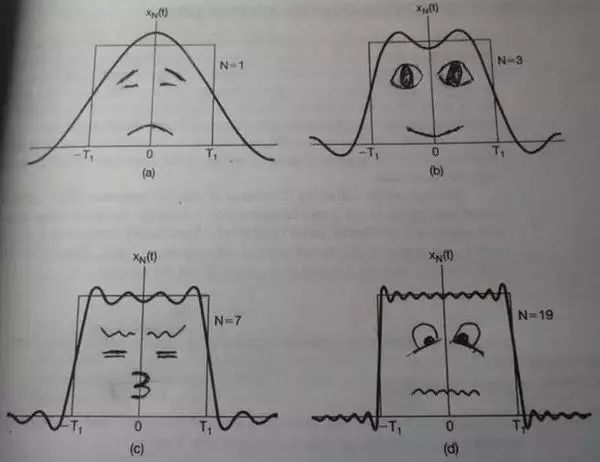
不同數(shù)量疊加后的效果

第一幅圖是一個(gè)郁悶的正弦波cos（x）；

第二幅圖是2個(gè)賣(mài)萌的正弦波的疊加cos(x)+a.cos(3x)；

第三幅圖是4個(gè)發(fā)春的正弦波的疊加；

第四幅圖是10個(gè)便秘的正弦波的疊加。

不是看到了正弦波數(shù)量越多，疊加后的波形越來(lái)越符合原方波。那么，如果是無(wú)限個(gè)正弦波進(jìn)行疊加呢？

二、歐拉公式

直截了當(dāng)，不管你記得不記得，我先把歐拉公式擺出來(lái)吧。

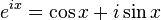
虛數(shù)i這個(gè)概念大家在高中就接觸過(guò)，但那時(shí)我們只知道它是-1的平方根，可是它真正的意義是什么呢?

這里有一條數(shù)軸，在數(shù)軸上有一個(gè)紅色的線段，它的長(zhǎng)度是1。當(dāng)它乘以3的時(shí)候，它的長(zhǎng)度發(fā)生了變化，變成了藍(lán)色的線段，而當(dāng)它乘以-1的時(shí)候，就變成了綠色的線段，或者說(shuō)線段在數(shù)軸上圍繞原點(diǎn)旋轉(zhuǎn)了180度。

我們知道乘-1其實(shí)就是乘了兩次i使線段旋轉(zhuǎn)了180度，那么乘一次i呢——答案很簡(jiǎn)單—旋轉(zhuǎn)了90度。

同時(shí)，我們獲得了一個(gè)垂直的虛數(shù)軸。實(shí)數(shù)軸與虛數(shù)軸共同構(gòu)成了一個(gè)復(fù)數(shù)的平面，也稱復(fù)平面。這樣我們就了解到，乘虛數(shù)i的一個(gè)功能—旋轉(zhuǎn)。

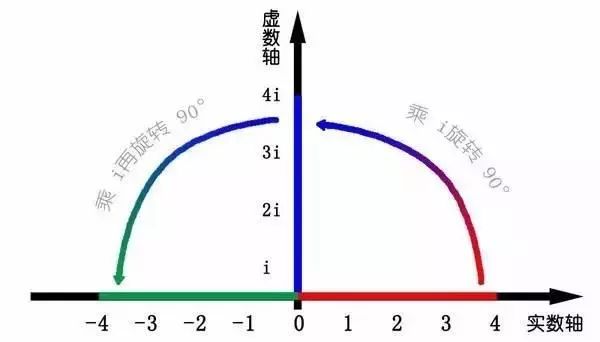
實(shí)數(shù)軸和虛數(shù)軸

在學(xué)習(xí)復(fù)變函數(shù)之前，我們接觸到都是實(shí)數(shù)；復(fù)變函數(shù)是向虛數(shù)進(jìn)行了延伸，而歐拉公式是這種延伸的橋梁。不單單是FT，它還在很多領(lǐng)域發(fā)揮了關(guān)鍵的作用。

三、FT的本質(zhì)

上面提到了FT的本質(zhì)，下面這樣圖就是把時(shí)域和頻域放在一個(gè)大坐標(biāo)系里進(jìn)行說(shuō)明。那么，F(xiàn)T的公式，就是變成了求得這些不同幅度的正弦的幅值。因?yàn)樗鼈兊念l率是基于原時(shí)域波形而有規(guī)律的變化，所以頻率是已知的。同時(shí)還有個(gè)為了符合原波形的幅度而引出的直流分量。求得了這些，也就是完成了整個(gè)的FT。

FT的本質(zhì)

FT公式：

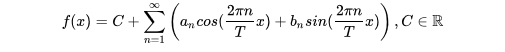
其中C就是上面提到的直流分量，an和bn就是不同頻率的正弦的幅度。

最后需要說(shuō)明的是，F(xiàn)T是DFT和FFT的基礎(chǔ)，只要先把FT的本質(zhì)掌握了，后面兩者只是對(duì)FT的具體應(yīng)用和實(shí)現(xiàn)的形式。