現代密碼協議規定只有授權參與者才可以獲得密鑰和訪問信息的權限。然而，通過侵入系統泄露密碼的方法層出不窮，給現代信息安全造成嚴重的威脅。對此問題，PUF不可克隆的優點，為信息安全提供了進一步的保障。例如：RO PUF、Arbiter PUF、SRAM PUF。通過把物理信息集成到電路設計從而實現PUF的設計，與現有RO PUF相比，PISO移位寄存器的運用減少了更多的硬件資源。由4位激勵能夠產生16位隨機響應，大大增加了激勵響應對的數目，而且通過FPGA測得內部漢明距離是符合要求的。

引言

加密是信息安全的一個分支，其中包括數據安全性、數據完整性和安全認證機制。加密技術的使用使得通信安全有了保障。發送方終端通過密鑰對數據進行加密，在接收終端以相同的密鑰或派生密鑰解密信息。加密體制依據解密與加密所用秘鑰是否相同，將其劃分為對稱和非對稱密碼兩種體制。在對稱密碼體制中，加密密鑰和解密密鑰是一樣的。而非對稱密碼體制中，加密密鑰和解密密鑰是分開的，不相同。加密的密鑰不應該受到環境的影響，應該是隨機的、可靠的以及抗側信道攻擊的。 一種基于PUF的密鑰產生機制如圖1所示。

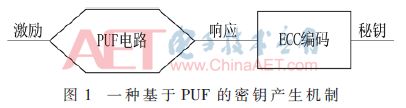
經典線性反饋移位寄存器用于隨機數生成。偽噪聲隨機數字發生器（PN-RNG）是利用初始種子產生隨機數序列的。由于有一組共同的初始種子，偽噪聲隨機數發生器（PN-RNG)產生的隨機序列并不隨機，如果有人存儲這些序列，根據序列之間的相關性，即PN-RNG在產生最大值之后開始產生相同的序列，對手可以預測到下一個序列[1]。加密密鑰是數據安全的關鍵，秘鑰一定是可信可靠的隨機數。真正可靠的密碼體系應該是：即便破譯者可以加密任何的明文，也沒法破譯密文。一般地，如果僅根據密文就可以推算出明文或密鑰，則稱這個密碼體制是可破譯的。基爾霍夫原則指出“一個密碼體制是安全的，其總的前提就是假設密碼分析者已經知道了密碼體制的算法，體制的安全性僅依賴于密鑰的保密”。現在的人喜歡依賴手機進行電子交易，所以信息安全得到了更多的關注。硅密鑰因為具有不可克隆的特點而被優選，不可克隆是指：即使用相同的材料也不能制造出2個性能相同的設備。2001年Srini Devadas(麻省理工學院CSAIL)提出了用物理不可克隆函數(PUF)來生成密鑰的IC。PUF是一種基于器件和工藝偏差的體系。從PUF系統可以產生不可預測的隨機數，不過PUF產生的隨機數必須經過編碼才能獲取想要的密鑰。PUF電路利用器件的特定屬性生成隨機數，這些屬性是無法克隆的，并且很難預測。根據半導體的任何可變屬性都可以用來構建PUF。延遲、頻率和SRAM上電初值的PUF，已在早期研究工作中有所研究，這些PUF[3]都反應了制造設備的隨機性變化。PUF電路必須能夠產生大量的激勵響應對。對于每個激勵響應都應該獨特而不可預測。對于不同的PUF，同樣的激勵生成的PUF響應應該都是不同的。PUF的性能可以用唯一性、可靠性和穩定性衡量。唯一性一般用內部漢明距離表示，理想值μ=0%。它代表了對于不同的PUF給予相同的激勵條件，得到響應之間的差異性。文獻[3]中展示了唯一性，用這種特性來識別電路。可靠性一般用片間漢明距離表示，理想情況下μ=0%。它代表對于同一個PUF，給予兩個相同的激勵，得到響應之間的差異性。穩定性表示響應受溫度、老化效應、電源電壓、噪聲等環境的影響。理想的響應應該是獨立于這些因素的[4]。

1典型RO-PUF

RO PUF是PUF中常見的應用之一，其基本結構單元是環形振蕩器(Ring-Oscillator，RO)。RO的構成如圖2所示。

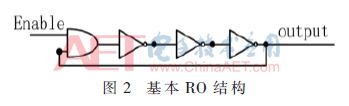
環形震蕩PUF是一個將激勵映射到響應的頻率變化函數。RO PUF是由于工藝偏差而產生的變化頻率來生成隨機數的。圖3給出了N個環振蕩器產生的不同頻率f1，f2，…fn，這里2個并行的多路復用器的選擇取決于輸入激勵。兩個多路復用器選定兩個不同的頻率 ，它們分別作為n位計數器的時鐘輸入。然后，兩個計數器對選定的兩個頻率開始計數。如果Q1>Q2響應為1，否則輸出響應為0。

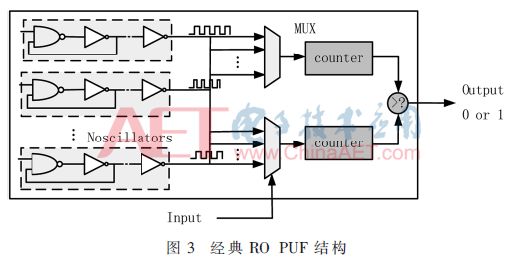
2本文提出的方案

本設計是利用不同數量的環形振蕩器而不是基于工藝偏差用相同數量的環形振蕩器來獲得變化的頻率。圖4所示的電路圖有3個工作模塊：(1)產生不同頻率的環形振蕩器，分別用不同階數的RO震蕩環產生5個不同的震蕩頻率；(2)映射階段，它是一個D觸發器的級聯，將環形振蕩器產生的任意兩個頻率作為D觸發器的數據輸入和時鐘輸入，輸出是一個采樣頻率。本設計中將F1、F2、F3、F4作為D觸發器的數據輸入，其對應的時鐘輸入分別為F2、F3、F4、F5；(3)選擇電路，基于多路復用器的選擇電路，根據激勵輸入選擇4個時鐘脈沖，并作為計數器的時鐘脈沖。在計數某個確定時間后，計數器值鎖存到PISO移位寄存器，在移位寄存器的每個時鐘有效邊沿產生1位響應，重復16次，獲得16位響應。圖4電路代表激勵響應對產生的方案，4位激勵被映射到16位響應，這個PUF是變化頻率和頻率映射階段的隨機函數。提出的電路結構在Virtex5上得到驗證。

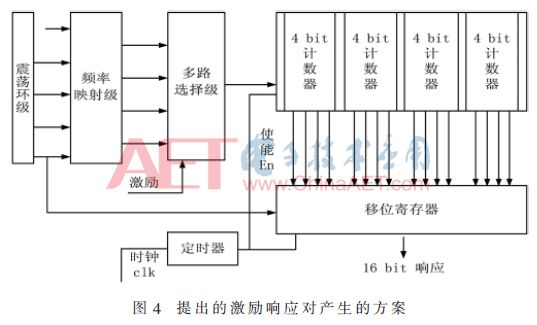
2.1環形振蕩器

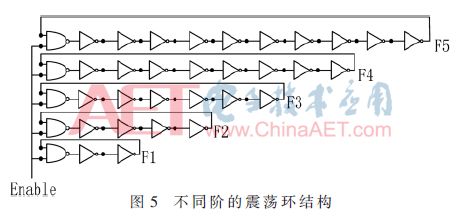
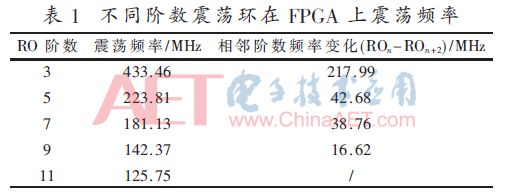
電路由5個具有奇數個反相器的環形振蕩器組成，目的是獲得不同的變化頻率。每個RO由圖5所示的nand門的輸入Enable控制，使能Enable信號為高開始振蕩。環形振蕩器由奇數個反相器構成，其頻率取決于反相器的階數，對于N階環形振蕩器，振蕩頻率為：Fosc=1/τpd=1/(2Nτp)，其中τpd=τphl+τplh，N為反向器的階數[5]。從表達式發現，隨著反相器階數的增加，頻率下降，頻率也彼此接近。表1顯示震蕩頻率隨著反相器數量的增加而發生變化。

2.2映射階段

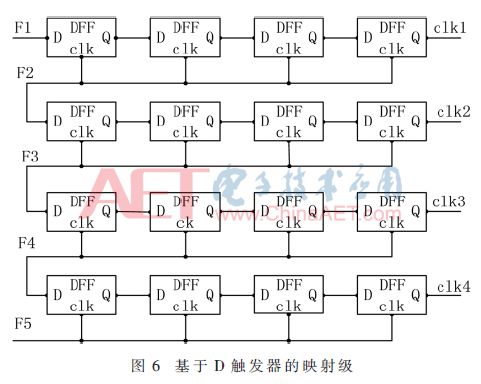
它是由4級D觸發器級聯，D觸發器將兩個頻率中一個作為數據輸入，另一個作為時鐘輸入，獲得一個采樣輸出，圖6所示的第一行4級D觸發器數據輸入端接F1，時鐘輸入接F2，采樣輸出記為CLK1。在本設計中使用時鐘上升沿觸發有效; 如果D觸發器時鐘上升沿比數據上升沿提前，輸出保持上次結果不變，如果時鐘上升沿比數據上升沿落后，則輸出與觸發器數據端輸入端一樣。同理，第二行、第三行、第四行4級級聯的D觸發器產生CLK2、CLK3、CLK4，產生的4個時鐘脈沖信號將用于下一級的頻率比較階段。由于振蕩器頻率不同，它們的邊緣到達時間是不可預測的，這就增加了更多的隨機性到PUF電路。在數據和時鐘邊緣同時到達的情況下將導致亞穩態，在下一個邊沿時鐘脈沖產生完全不可預測的電路輸出（高或低）。并且本文采用的是慢時鐘采快時鐘，根據麥奎斯特采樣定理，肯定會有信號遺漏，但是我們并不是想要最后得到完整的數據信號，僅僅是利用丟失信號的不確定性來增加PUF電路的隨機性。

2.3選擇電路

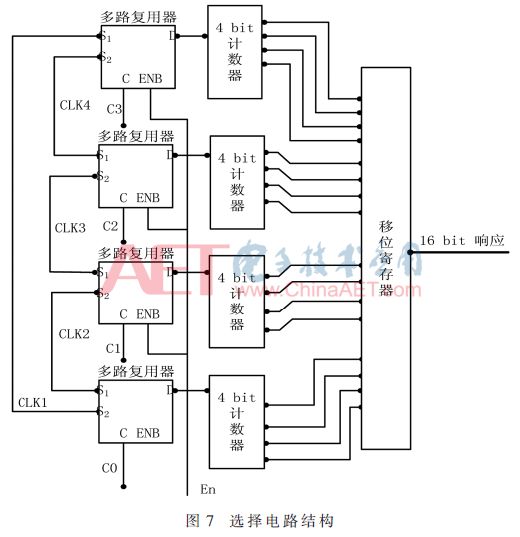
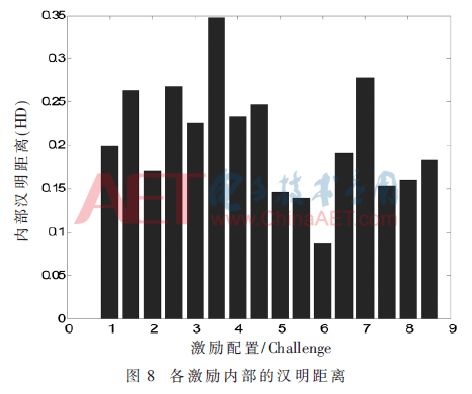
圖7所示電路是多路復用器構成的選擇電路。時鐘上升沿到來計數器向上計數。在計數某個確定時間后，計數器值鎖存到PISO移位寄存器，在移位寄存器的每個時鐘有效邊沿產生1位響應，重復16次，獲得16位響應。圖8給出了16個激勵的內部漢明距離，這幾乎是理想的值。本文提出的PUF結構與現有的RO PUF相比，需要更少的硬件資源。圖3顯示了2個計數器產生1位響應的RO結構。要有16位響應，它需要32個計數器和16個比較器并行工作。并且提出的PUF結構相對于RO PUF在計數階段消除了硬件復雜性，并從單個計數器和PISO移位寄存器直接產生16位響應。

本文提出了一種新穎的基于硬件的產生激勵響應對的RO PUF結構，其結合電路變化而不是工藝偏差。運用頻率映射與PUF結合的策略產生隨機性響應，響應的內部漢明距離幾乎達到理想值。PUF的早期設計中2個計數器產生1位響應，當前設計中用相同位數的計數器產生16位響應。在接下來的研究中計數器和PISO移位寄存器的大小可以增強到255位，為AES加密算法生成128位密鑰。

3實驗與分析

本文將上述方案在FPGA平臺上進行實驗測試，實驗開發板：Xilinx Virtex5，開發軟件：集成開發環境ISE，仿真工具Modelsim，測試和分析工具ChipScope；開發語言：Verilog HDL。經過XST綜合后的FPGA配置文件下載到開發板上，時鐘周期是50 ns，定時器定時時間為0.512 μs。用ChipScope 軟件抓取輸入激勵與其對應輸出響應的波形圖。通過ChipScope 導出的波形圖，解析出激勵-響應對。在測試過程中，對電路進行了50 次測試，每次測試能夠得到16個激勵-響應對，對同一個激勵產生的50個響應計算內部漢明距離，結果表明，該電路對于同一激勵的響應內部漢明距離最大為0.277 8，最小可以達到0.080 0，大部分分布在0.200 0左右，文獻[14]中測得的內部漢明距離9次達到0.310 0，6次達到0.190 0，1次達到0.250 0，所以比較文獻[14]，本文設計的PUF較優，該設計滿足PUF函數的相關要求。

4結論

本文的設計是通過把物理信息集成到電路設計從而實現PUF的設計，與現有RO PUF相比，PISO位寄存器的運用減少了更多的硬件資源。由4位激勵能夠產生16位隨機響應，大大增加了激勵響應對的數目，也即增加了ID的數量，安全性得到提高。并且經由FPGA驗證本文改良后的RO PUF具有更高的“片內穩定性”。環境溫度、供電電壓是影響片內穩定性的重要因素，確保ID不隨溫度、電壓發生變化，并且精確可重復生成是未來研究的方向。