1 原理

1.1 引入

首先，在引入LR(Logistic Regression)模型之前，非常重要的一個概念是，該模型在設計之初是用來解決0/1二分類問題，雖然它的名字中有回歸二字，但只是在其線性部分隱含地做了一個回歸，最終目標還是以解決分類問題為主。

為了較好地掌握 logistic regression 模型，有必要先了解 線性回歸模型 和 梯度下降法 兩個部分的內容，可參考以下兩篇文章：

線性回歸 —— Liner Regression

梯度下降法 —— 經典的優化方法

先回想一下線性回歸，線性回歸模型幫助我們用最簡單的線性方程實現了對數據的擬合，然而，這只能完成回歸任務，無法完成分類任務，那么 logistics regression 就是在線性回歸的基礎上添磚加瓦，構建出了一種分類模型。

如果在線性模型 ( 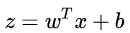) 的基礎上做分類，比如二分類任務，即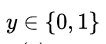，直覺上我們會怎么做？最直觀的，可以將線性模型的輸出值再套上一個函數 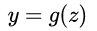，最簡單的就是“單位階躍函數”(unit-step function)，如下圖中紅色線段所示。

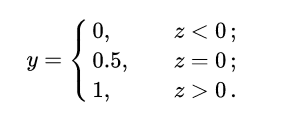
也就是把 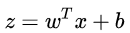看作為一個分割線，大于 z 的判定為類別0，小于 z 的判定為類別1。

但是，這樣的分段函數數學性質不太好，它既不連續也不可微。我們知道，通常在做優化任務時，目標函數最好是連續可微的。那么如何改進呢？

這里就用到了對數幾率函數 (形狀如圖中黑色曲線所示)：

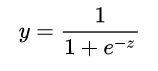
單位階躍函數與對數幾率函數（來源于周志華《機器學習》）

它是一種“Sigmoid”函數，Sigmoid 函數這個名詞是表示形式S形的函數，對數幾率函數就是其中最重要的代表。這個函數相比前面的分段函數，具有非常好的數學性質，其主要優勢如下：

使用該函數做分類問題時，不僅可以預測出類別，還能夠得到近似概率預測。這點對很多需要利用概率輔助決策的任務很有用。

對數幾率函數是任意階可導函數，它有著很好的數學性質，很多數值優化算法都可以直接用于求取最優解。

總的來說，模型的完全形式如下：

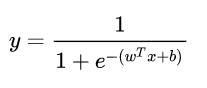
其實，LR 模型就是在擬合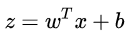

1.2 損失函數

對于任何機器學習問題，都需要先明確損失函數，LR模型也不例外，在遇到回歸問題時，通常我們會直接想到如下的損失函數形式 (平均誤差平方損失 MSE)：

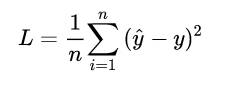
但在 LR 模型要解決的二分類問題中，損失函數式什么樣的呢？先給出這個損失函數的形式，可以看一看思考一下，然后再做解釋。

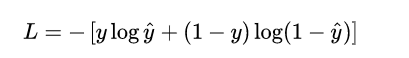
這個損失函數通常稱作為 對數損失 (logloss)，這里的對數底為自然對數 e ，其中真實值 y是有 0/1 兩種情況，而推測值 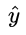由于借助對數幾率函數，其輸出是介于0~1之間連續概率值。仔細查看，不難發現，當真實值 y=0 時，第一項為0，當真實值 y=1時，第二項為0，所以，這個損失函數其實在每次計算時永遠都只有一項在發揮作用，那這不就可以轉換為分段函數了嗎，分段的形式如下：

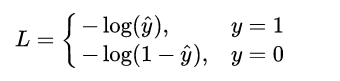
不難發現，當真實值 y 為1時，輸出值 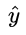越接近1，則 L 越小，當真實值 y 為 0 時，輸出值 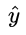越接近于0，則 L 越小 (可自己手畫一下 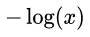函數的曲線)。該分段函數整合之后就是上面我們所列出的 logloss 損失函數的形式。

1.3 優化求解

現在我們已經確定了模型的損失函數，那么接下來就是根據這個損失函數，不斷優化模型參數從而獲得擬合數據的最佳模型。

重新看一下損失函數，其本質上是 L 關于模型中線性方程部分的兩個參數 w 和 b 的函數：

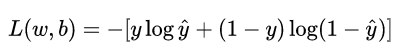
其中，

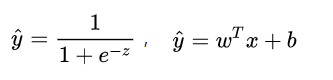
現在的學習任務轉化為數學優化的形式即為：

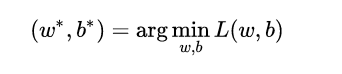
由于損失函數連續可微，我們就可以借助 梯度下降法 進行優化求解，對于連個核心參數的更新方式如下：

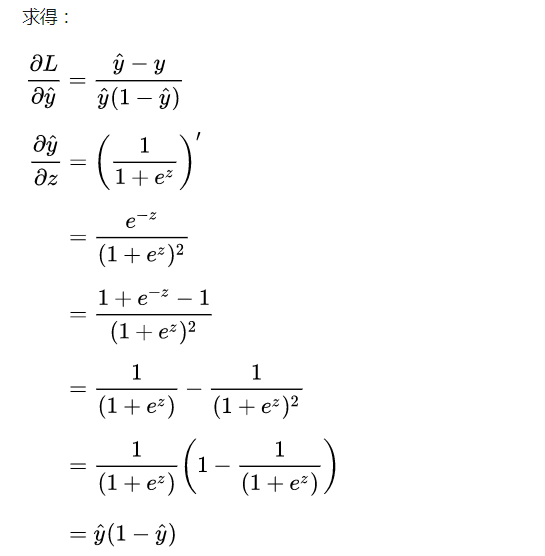
計算到這里，很有意思的事情發生了：

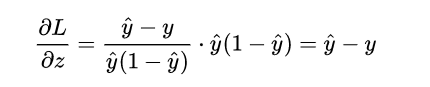
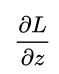計算了半天原來變得如此簡單，就是推測值 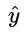和真實值 Y 之間的差值，其實這也是得益于對數幾率函數本身很好的數學性質。

再接再厲，求得：

2 代碼實現

下面我們開始用 python 自己實現一個簡單的 LR 模型。

完整代碼可參考：[link]

首先，建立 logistic_regression.py 文件，構建 LR 模型的類，內部實現了其核心的優化函數。

# -*- coding: utf-8 -*-import numpy as npclass LogisticRegression(object): def __init__(self, learning_rate=0.1, max_iter=100, seed=None): self.seed = seed self.lr = learning_rate self.max_iter = max_iter def fit(self, x, y): np.random.seed(self.seed) self.w = np.random.normal(loc=0.0, scale=1.0, size=x.shape[1]) self.b = np.random.normal(loc=0.0, scale=1.0) self.x = x self.y = y for i in range(self.max_iter): self._update_step() # print('loss: \t{}'.format(self.loss())) # print('score: \t{}'.format(self.score())) # print('w: \t{}'.format(self.w)) # print('b: \t{}'.format(self.b)) def _sigmoid(self, z): return 1.0 / (1.0 + np.exp(-z)) def _f(self, x, w, b): z = x.dot(w) + b return self._sigmoid(z) def predict_proba(self, x=None): if x is None: x = self.x y_pred = self._f(x, self.w, self.b) return y_pred def predict(self, x=None): if x is None: x = self.x y_pred_proba = self._f(x, self.w, self.b) y_pred = np.array([0 if y_pred_proba[i] < 0.5 else 1 for i in range(len(y_pred_proba))]) ? ? ? ?return y_pred ? ?def score(self, y_true=None, y_pred=None): ? ? ? ?if y_true is None or y_pred is None: ? ? ? ? ? ?y_true = self.y ? ? ? ? ? ?y_pred = self.predict() ? ? ? ?acc = np.mean([1 if y_true[i] == y_pred[i] else 0 for i in range(len(y_true))]) ? ? ? ?return acc ? ?def loss(self, y_true=None, y_pred_proba=None): ? ? ? ?if y_true is None or y_pred_proba is None: ? ? ? ? ? ?y_true = self.y ? ? ? ? ? ?y_pred_proba = self.predict_proba() ? ? ? ?return np.mean(-1.0 * (y_true * np.log(y_pred_proba) + (1.0 - y_true) * np.log(1.0 - y_pred_proba))) ? ?def _calc_gradient(self): ? ? ? ?y_pred = self.predict() ? ? ? ?d_w = (y_pred - self.y).dot(self.x) / len(self.y) ? ? ? ?d_b = np.mean(y_pred - self.y) ? ? ? ?return d_w, d_b ? ?def _update_step(self): ? ? ? ?d_w, d_b = self._calc_gradient() ? ? ? ?self.w = self.w - self.lr * d_w ? ? ? ?self.b = self.b - self.lr * d_b ? ? ? ?return self.w, self.b

然后，這里我們創建了一個 文件，單獨用于創建模擬數據，并且內部實現了訓練/測試數據的劃分功能。

# -*- coding: utf-8 -*-import numpy as npdef generate_data(seed): np.random.seed(seed) data_size_1 = 300 x1_1 = np.random.normal(loc=5.0, scale=1.0, size=data_size_1) x2_1 = np.random.normal(loc=4.0, scale=1.0, size=data_size_1) y_1 = [0 for _ in range(data_size_1)] data_size_2 = 400 x1_2 = np.random.normal(loc=10.0, scale=2.0, size=data_size_2) x2_2 = np.random.normal(loc=8.0, scale=2.0, size=data_size_2) y_2 = [1 for _ in range(data_size_2)] x1 = np.concatenate((x1_1, x1_2), axis=0) x2 = np.concatenate((x2_1, x2_2), axis=0) x = np.hstack((x1.reshape(-1,1), x2.reshape(-1,1))) y = np.concatenate((y_1, y_2), axis=0) data_size_all = data_size_1+data_size_2 shuffled_index = np.random.permutation(data_size_all) x = x[shuffled_index] y = y[shuffled_index] return x, ydef train_test_split(x, y): split_index = int(len(y)*0.7) x_train = x[:split_index] y_train = y[:split_index] x_test = x[split_index:] y_test = y[split_index:] return x_train, y_train, x_test, y_test

最后，創建 train.py 文件，調用之前自己寫的 LR 類模型實現分類任務，查看分類的精度。

# -*- coding: utf-8 -*-import numpy as npimport matplotlib.pyplot as pltimport data_helperfrom logistic_regression import *# data generationx, y = data_helper.generate_data(seed=272)x_train, y_train, x_test, y_test = data_helper.train_test_split(x, y)# visualize data# plt.scatter(x_train[:,0], x_train[:,1], c=y_train, marker='.')# plt.show()# plt.scatter(x_test[:,0], x_test[:,1], c=y_test, marker='.')# plt.show()# data normalizationx_train = (x_train - np.min(x_train, axis=0)) / (np.max(x_train, axis=0) - np.min(x_train, axis=0))x_test = (x_test - np.min(x_test, axis=0)) / (np.max(x_test, axis=0) - np.min(x_test, axis=0))# Logistic regression classifierclf = LogisticRegression(learning_rate=0.1, max_iter=500, seed=272)clf.fit(x_train, y_train)# plot the resultsplit_boundary_func = lambda x: (-clf.b - clf.w[0] * x) / clf.w[1]xx = np.arange(0.1, 0.6, 0.1)plt.scatter(x_train[:,0], x_train[:,1], c=y_train, marker='.')plt.plot(xx, split_boundary_func(xx), c='red')plt.show()# loss on test sety_test_pred = clf.predict(x_test)y_test_pred_proba = clf.predict_proba(x_test)print(clf.score(y_test, y_test_pred))print(clf.loss(y_test, y_test_pred_proba))# print(y_test_pred_proba)

輸出結果圖如下：

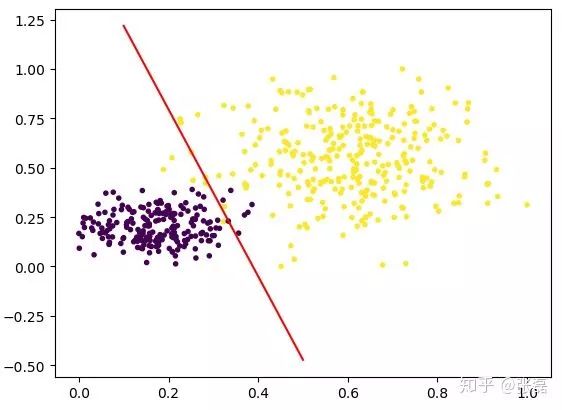
輸出的分類結果圖

紅色直線即為 LR 模型中的線性方程，所以本質上 LR 在做的就是不斷擬合這條紅色的分割邊界使得邊界兩側的類別正確率盡可能高。因此，LR 其實是一種線性分類器，對于輸入數據的分布為非線性復雜情況時，往往需要我們采用更復雜的模型，或者繼續在特征工程上做文章。