??Abstract：最近課業(yè)內(nèi)的任務不是很多，又臨近暑假了，就在網(wǎng)上搜了一些有關于機器學習和深度學習的課程進行學習。網(wǎng)上的資料非常繁多，很難甄別，我也是貨比三家進行學習。這是這個系列的第一個筆記，是關于貝葉斯和MCMC一些數(shù)學原理的講解和代碼的實現(xiàn)，希望能夠深入淺出，敘述的容易讓人理解。…

淺談貝葉斯

不論是學習概率統(tǒng)計還是機器學習的過程中，貝葉斯總是是繞不過去的一道坎，大部分人在學習的時候都是在強行地背公式和套用方法，沒有真正去理解其牛逼的思想內(nèi)涵。我看了一下 Chalmers 一些涉及到貝葉斯統(tǒng)計的課程，content 里的第一條都是Philosophy of Bayesian statistics。

歷史背景

什么事都要從頭說起，貝葉斯全名為托馬斯·貝葉斯(Thomas Bayes，1701-1761),是一位與牛頓同時代的牧師，是一位業(yè)余數(shù)學家，平時就思考些有關上帝的事情，當然，統(tǒng)計學家都認為概率這個東西就是上帝在擲骰子。當時貝葉斯發(fā)現(xiàn)了古典統(tǒng)計學當中的一些缺點，從而提出了自己的“貝葉斯統(tǒng)計學”，但貝葉斯統(tǒng)計當中由于引入了一個主觀因素（先驗概率，下文會介紹），一點都不被當時的人認可。直到20世紀中期，也就是快200年后了，統(tǒng)計學家在古典統(tǒng)計學中遇到了瓶頸，伴隨著計算機技術的發(fā)展，當統(tǒng)計學家使用貝葉斯統(tǒng)計理論時發(fā)現(xiàn)能解決很多之前不能解決的問題，從而貝葉斯統(tǒng)計學一下子火了起來，兩個統(tǒng)計學派從此爭論不休。

什么是概率？

什么是概率這個問題似乎人人都覺得自己知道，卻有很難說明白。比如說我問你擲一枚硬幣為正面的概率為多少？，大部分人第一反應就是50%的幾率為正。不好意思，首先這個答案就不正確，只有當材質(zhì)均勻時硬幣為正面的幾率才是50%（所以不要覺得打麻將的時候那個骰子每面的幾率是相等的，萬一被做了手腳呢）。好，那現(xiàn)在假設硬幣的材質(zhì)是均勻的，那么為什么正面的幾率就是50%呢？有人會說是因為我擲了1000次硬幣，大概有492次是正面，508次是反面，所以近似認為是50%，說得很好（擲了1000次我也是服你）。

擲硬幣的例子說明了古典統(tǒng)計學的思想，就是概率是基于大量實驗的，也就是大數(shù)定理。那么現(xiàn)在再問你，有些事件，例如：明天下雨的概率是30%；A地會發(fā)生地震的概率是 5%；一個人得心臟病的概率是 40%……這些概率怎么解釋呢？難道是A地真的 100 次的機會里，地震了 5 次嗎？肯定不是這樣，所以古典統(tǒng)計學就無法解釋了。再回到擲硬幣的例子中，如果你沒有機會擲 1000 次這么多次，而是只擲了 3 次，可這 3 次又都是正面，那該怎么辦？難道這個正面的概率就是 100% 了嗎？這也是古典統(tǒng)計學的弊端。

舉個例子：生病的幾率

一種癌癥，得了這個癌癥的人被檢測出為陽性的幾率為 90%，未得這種癌癥的人被檢測出陰性的幾率為 90%，而人群中得這種癌癥的幾率為 1%，一個人被檢測出陽性，問這個人得癌癥的幾率為多少？

猛地一看，被檢查出陽性，而且得癌癥的話陽性的概率是 90%，那想必這個人應該是難以幸免了。那我們接下來就算算看。

我們用A表示事件 “測出為陽性”, 用B1表示“得癌癥”,B2表示“未得癌癥”。根據(jù)題目，我們知道如下信息:

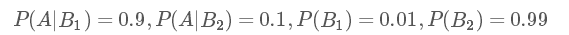
那么我們現(xiàn)在想得到的是已知為陽性的情況下，得癌癥的幾率P(B1,A):

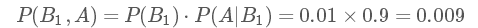
P(B1,A)表示的是聯(lián)合概率，得癌癥且檢測出陽性的概率是人群中得癌癥的概率乘上得癌癥時測出是陽性的幾率，是 0.009。同理可得得癌癥且檢測出陽性的概率：

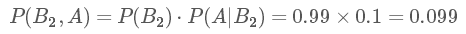
這個概率是什么意思呢？其實是指如果人群中有 1000 個人，檢測出陽性并且得癌癥的人有 9 個，檢測出陽性但未得癌癥的人有 99 個。可以看出，檢測出陽性并不可怕，不得癌癥的是絕大多數(shù)的，這跟我們一開始的直覺判斷是不同的！可直到現(xiàn)在，我們并沒有得到所謂的“在檢測出陽性的前提下得癌癥的概率”，怎么得到呢？很簡單，就是看被測出為陽性的這 108(9+99) 人里，9 人和 99 人分別占的比例就是我們要的,也就是說我們只需要添加一個歸一化因子(normalization)就可以了。所以陽性得癌癥的概率P(B1|A)為：

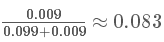
陽性未得癌癥的概率P(B2|A)為：

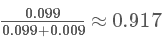
這里P(B1|A)，P(B2|A)中間多了這一豎線||成為了條件概率，而這個概率就是貝葉斯統(tǒng)計中的后驗概率！而人群中患癌癥與否的概率P(B1),P(B2)就是先驗概率！我們知道了先驗概率，根據(jù)觀測值(observation)，也可稱為 test evidence：是否為陽性，來判斷得癌癥的后驗概率，這就是基本的貝葉斯思想，我們現(xiàn)在就能得出本題的后驗概率的公式為：

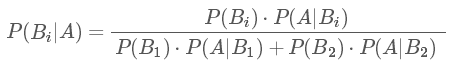
由此就能得到如下的貝葉斯公式的一般形式。

貝葉斯公式

我們把上面例題中的A變成樣本(sample)x, 把B變成參數(shù)(parameter)θ, 我們便得到我們的貝葉斯公式：

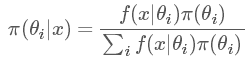
??可以看出上面這個例子中，B事件的分布是離散的，所以在分母用的是求和符號∑。那如果我們的參數(shù)θ的分布是連續(xù)的呢？沒錯，那就要用積分，于是我們終于得到了真正的貝葉斯公式：

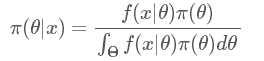
其中 π 指的是參數(shù)的概率分布，π(θ) 指的是先驗概率，π(θ|x) 指的是后驗概率，f(x|θ)指的是我們觀測到的樣本的分布，也就是似然函數(shù)(likelihood)，記住豎線 |左邊的才是我們需要的。其中積分求的區(qū)間指的是參數(shù) θ 所有可能取到的值的域，所以可以看出后驗概率 π(θ|x) 是在知道 x 的前提下在域內(nèi)的一個關于θ 的概率密度分布，每一個θ 都有一個對應的可能性(也就是概率)。

理解貝葉斯公式

這個公式應該在概率論書中就有提到，反正當時我也只是死記硬背住，然后遇到題目就套用。甚至在 Chalmers 學了一門統(tǒng)計推斷的課講了貝葉斯，大部分時間我還是在套用公式，直到后來結(jié)合了一些專門講解貝葉斯的課程和資料才有了一些真正的理解。要想理解這個公式，首先要知道這個豎線 | 的兩側(cè)一會是 x|θ ，一會是 θ|x 到底指的是什么，或者說似然函數(shù)和參數(shù)概率分布到底指的是什么。

似然函數(shù)

首先來看似然函數(shù) f(x|θ)，似然函數(shù)聽起來很陌生，其實就是我們在概率論當中看到的各種概率分布 f(x)，那為什么后面要加個參數(shù)|θ 呢？我們知道，擲硬幣這個事件是服從伯努利分布的 Ber(p) , n次的伯努利實驗就是我們熟知的二項分布 Bin(n,p), 這里的p就是一個參數(shù)，原來我們在做實驗之前，這個參數(shù)就已經(jīng)存在了(可以理解為上帝已經(jīng)定好了)，我們抽樣出很多的樣本 x 是為了找出這個參數(shù)，我們上面所說的擲硬幣的例子，由于我們擲了 1000 次有 492 次是正面，根據(jù)求期望的公式 n?p=μ (492就是我們的期望)可以得出參數(shù) p 為

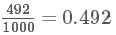
所以我們才認為正面的概率是近似 50% 的。

現(xiàn)在我們知道了，其實我們觀測到樣本 x 的分布是在以某個參數(shù) θ 為前提下得出來的，所以我們記為 f(x|θ)，只是我們并不知道這個參數(shù)是多少。所以參數(shù)估計成為了統(tǒng)計學里很大的一個課題，古典統(tǒng)計學中常用的方法有兩種：矩方法(momnet)和最大似然估計(maximum likelihood estimate, mle)，我們常用的像上面擲硬幣例子中求均值的方法，本質(zhì)就是矩估計方法，這是基于大數(shù)定理的。而統(tǒng)計學中更廣泛的是使用最大似然估計的方法，原理其實很簡單，在這簡單說一下：假設我們有 n 個樣本 x1,x2,x3,…,xn，它們每一個變量都對應一個似然函數(shù):

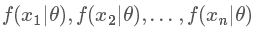
我們現(xiàn)在把這些似然函數(shù)乘起來:

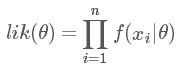
我們只要找到令 lik(θ) 這個函數(shù)最大的 θ 值，便是我們想要的參數(shù)值(具體計算參考[2]中p184)。

后驗分布(Posterior distribution)

現(xiàn)在到了貝葉斯的時間了。以前我們想知道一個參數(shù)，要通過大量的觀測值才能得出，而且是只能得出一個參數(shù)值。而現(xiàn)在運用了貝葉斯統(tǒng)計思想，這個后驗概率分布 π(θ|x) 其實是一系列參數(shù)值 θ 的概率分布，再說簡單點就是我們得到了許多個參數(shù) θ 及其對應的可能性，我們只需要從中選取我們想要的值就可以了：有時我們想要概率最大的那個參數(shù)，那這就是后驗眾數(shù)估計(posterior mode estimator)；有時我們想知道參數(shù)分布的中位數(shù)，那這就是后驗中位數(shù)估計(posterior median estimator);有時我們想知道的是這個參數(shù)分布的均值，那就是后驗期望估計。這三種估計沒有誰好誰壞，只是提供了三種方法得出參數(shù)，看需要來選擇。現(xiàn)在這樣看來得到的參數(shù)是不是更具有說服力？

置信區(qū)間和可信區(qū)間

在這里我想提一下置信區(qū)間(confidence interval, CI) 和可信區(qū)間(credibility interval,CI),我覺得這是剛學貝葉斯時候非常容易弄混的概念。

再舉個例子：一個班級男生的身高可能服從某種正態(tài)分布 N(μ,σ2),然后我們把全班男生的身高給記錄下來，用高中就學過的求均值和方差的公式就可以算出來這兩個參數(shù)，要知道我們真正想知道的是這個參數(shù) μ,σ2，當然樣本越多，得出的結(jié)果就接近真實值(其實并沒有人知道什么是真實值，可能只有上帝知道)。等我們算出了均值和方差，我們這時候一般會構(gòu)建一個95%或者90%的置信區(qū)間，這個置信區(qū)間是對于樣本 x來說的，我只算出了一個 μ 和 一個 σ 參數(shù)值的情況下，95% 的置信區(qū)間意味著在這個區(qū)間里的樣本是可以相信是服從以 μ,σ 為參數(shù)的正態(tài)分布的，一定要記住置信區(qū)間的概念中是指一個參數(shù)值的情況下！

而我們也會對我們得到的后驗概率分布構(gòu)造一個 90% 或 95% 的區(qū)間，稱之為可信區(qū)間。這個可信區(qū)間是對于參數(shù) θ來說的，我們的到了 很多的參數(shù)值，取其中概率更大一些的90%或95%，便成了可信區(qū)間。

先驗分布(Prior distribution)

說完了后驗分布，現(xiàn)在就來說說先驗分布。先驗分布就是你在取得實驗觀測值以前對一個參數(shù)概率分布的主觀判斷，這也就是為什么貝葉斯統(tǒng)計學一直不被認可的原因，統(tǒng)計學或者數(shù)學都是客觀的，怎么能加入主觀因素呢？但事實證明這樣的效果會非常好！

再拿擲硬幣的例子來看(怎么老是拿這個舉例，是有多愛錢。。。)，在扔之前你會有判斷正面的概率是50%，這就是所謂的先驗概率，但如果是在打賭，為了讓自己的描述準確點，我們可能會說正面的概率為 0.5 的可能性最大，0.45 的幾率小點，0.4 的幾率再小點，0.1 的幾率幾乎沒有等等，這就形成了一個先驗概率分布。

那么現(xiàn)在又有新的問題了，如果我告訴你這個硬幣的材質(zhì)是不均勻的，那正面的可能性是多少呢？這就讓人犯糊涂了，我們想有主觀判斷也無從下手，于是我們就想說那就先認為 0~1 之間每一種的可能性都是相同的吧，也就是設置成 0~1 之間的均勻分布Uni(0,1) 作為先驗分布吧，這就是貝葉斯統(tǒng)計學當中的無信息先驗(noninformative prior)！那么下面我們就通過不斷擲硬幣來看看，這個概率到是多少，貝葉斯過程如下：

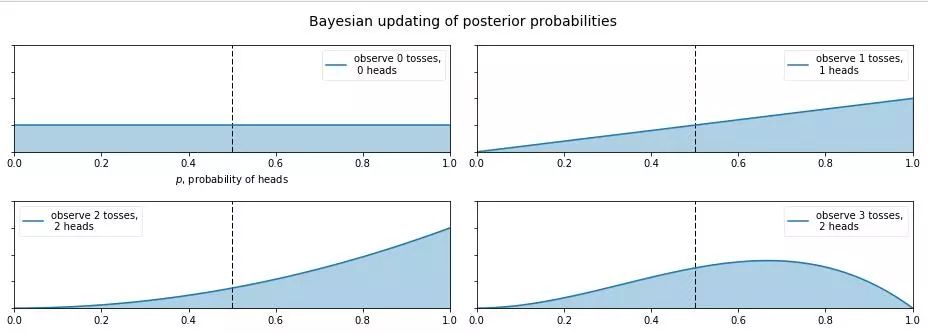
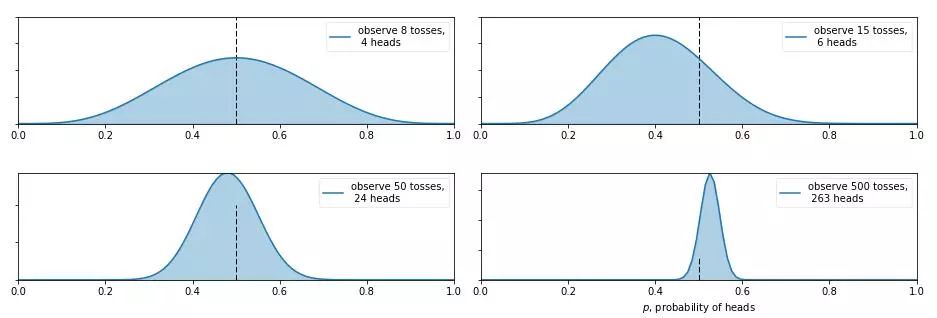
從圖中我們可以看出，0 次試驗的時候就是我們的先驗假設——均勻分布，然后擲了第一次是正面，于是概率分布傾向于 1，第二次又是正，概率是 1的可能性更大了，但注意：這時候在 0.5 的概率還是有的，只不過概率很小，在 0.2 的概率變得更小。第三次是反面，于是概率分布被修正了一下，從為1的概率最大變成了 2/3 左右最大(3次試驗，2 次正 1 次反當然概率是2/3的概率最大)。再下面就是進行更多次的試驗，后驗概率不斷根據(jù)觀測值在改變，當次數(shù)很大的時候，結(jié)果趨向于 0.5 (哈哈，結(jié)果這還是一枚普通的硬幣，不過這個事件告訴我們，直覺是不可靠的，一定親自實驗才行~)。

有的人會說，這還不是在大量數(shù)據(jù)下得到了正面概率為 0.5 嘛，有什么好稀奇的？注意了！畫重點了！(敲黑板) 記住，不要和一個統(tǒng)計學家或者數(shù)學家打賭！跑題了，跑題了。。。說回來，我們上面就說到了古典概率學的弊端就是如果擲了 2 次都是正面，那我們就會認為正面的概率是 1，而在貝葉斯統(tǒng)計學中，如果我們擲了 2 次都是正面，只能說明正面是1的可能性最大，但還是有可能為 0.5, 0.6, 0.7 等等的，這就是對古典統(tǒng)計學的一種完善和補充，于是我們也就是解釋了，我們所謂的地震的概率為 5%；生病的概率為 10% 等等這些概率的意義了，這就是貝葉斯統(tǒng)計學的哲學思想。

共軛先驗(Conjugate prior)

共軛先驗應該是每一個貝葉斯統(tǒng)計初學者最頭疼的問題，我覺得沒有“之一”。這是一個非常大的理論體系，我試著用一些簡單的語言進行描述，關鍵是去理解其思想。

繼續(xù)拿擲硬幣的例子，這是一個二項試驗 Bin(n,p)，所以其似然函數(shù)為:

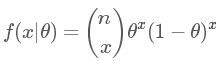
在我們不知道情況時就先假設其先驗分布為均勻分布 Uni(0,1)，即：

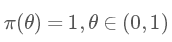
那現(xiàn)在根據(jù)貝葉斯公式求后驗概率分布：

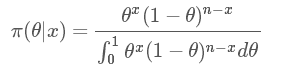
我們得到結(jié)果為:

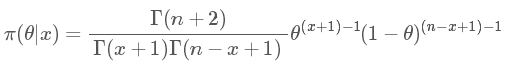
這么一大串是什么呢？其實就是大名鼎鼎的貝塔分布(Beta distribution)。 簡寫就是 Be(x+1,n?x+1)。 比如我擲了10 次(n=10)，5次正(x=5),5 次反，那么結(jié)果就是 Be(6,6), 這個分布的均值就是

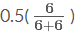
很符合我們想要的結(jié)果。

現(xiàn)在可以說明，我們把主觀揣測的先驗概率定為均勻分布是合理的，因為我們在對一件事物沒有了解的時候，先認為每種可能性都一樣是非常說得通的。有人會認為，既然無信息先驗是說得通的，而且貝葉斯公式會根據(jù)我們的觀測值不斷更新后驗概率，那是不是我們隨便給一個先驗概率都可以呢？當然……不行！！這個先驗概率是不能瞎猜的，是需要根據(jù)一些前人的經(jīng)驗和常識來判斷的。比如我隨便猜先驗為一個分段函數(shù)：

靠，是不是很變態(tài)的一個函數(shù)…就是假設一個極端的情況，如果你把這個情況代入貝葉斯公式，結(jié)果是不會好的(當然我也不知道該怎么計算)。

這個例子中，我看到了可能的后驗分布是 Beta 分布，看起來感覺有點像正態(tài)分布啊，那我們用正態(tài)分布作為先驗分布可以嗎？這個是可以的(所以要學會觀察)。可如果我們把先驗分布為正態(tài)分布代入到貝葉斯公式，那計算會非常非常麻煩，雖然結(jié)果可能是合理的。那怎么辦？不用擔心，因為我們有共軛先驗分布！

繼續(xù)拿上面這個例子，如果我們把先驗分布 π(θ) 設為貝塔分布 Beta(a,b)，結(jié)果是什么呢？我就不寫具體的計算過程啦，直接給結(jié)果：

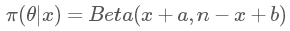
有沒有看到，依然是貝塔分布，結(jié)果只是把之前的 1 換成了 a 和 b(聰明的你可能已經(jīng)發(fā)現(xiàn)，其實我們所說的均勻分布 Uni(0,1) 等價于 Beta(1,1),兩者是一樣的)。

由此我們便可以稱二項分布的共軛先驗分布為貝塔分布！注意！接著畫重點！：共軛先驗這個概念必須是基于似然函數(shù)來討論的，否則沒有意義！好，那現(xiàn)在有了共軛先驗，然后呢？作用呢？這應該是很多初學者的疑問。

現(xiàn)在我們來看，如果你知道了一個觀測樣本的似然函數(shù)是二項分布的，那我們把先驗分布直接設為 Beta(a,b) ，于是我們就不用計算復雜的含有積分的貝葉斯公式便可得到后驗分布 Beta (x+a,n?x+b) 了！！！只需要記住試驗次數(shù)n，和試驗成功事件次數(shù)x就可以了！互為共軛的分布還有一些，但都很復雜，用到的情況也很少，推導過程也極其復雜，有興趣的可以自行搜索。我說的這個情況是最常見的！

注意一下，很多資料里會提到一個概念叫偽計數(shù)(pseudo count),這里的偽計數(shù)值得就是a,b對后驗概率分布的影響，我們會發(fā)現(xiàn)如果我們?nèi)?Beta(1,1) ，這個先驗概率對結(jié)果的影響會很小，可如果我們設為 Beta(100,100)，那么我們做 10 次試驗就算是全是正面的，后驗分布都沒什么變化。

樸素貝葉斯分類器(Naive Bayes classifier)和scikit-learn的簡單使用

在機器學習中你應該會看到有一個章節(jié)是講樸素貝葉斯分類器的(把naive翻譯成樸素我也是服了啊，以后我們可以“夸”某某人好樸素啊)。具體的數(shù)學原理在周志華老師的西瓜書《機器學習》的第7章有詳細解釋，其實就是利用了基本的貝葉斯理論，跟上面說的差不多，只不過更加說明的怎樣去實踐到機器學習中。下面就直接簡單說一下Python中有個機器學習庫 scikit-learn 中樸素貝葉斯分類器的簡單實用。例子參考的是 scikit-learn 官網(wǎng)的GaussianNB 頁面。

直接看代碼：

import numpy as npX = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])Y = np.array([1, 1, 1, 2, 2, 2])from sklearn.naive_bayes import GaussianNB #導入GaussianNBclf = GaussianNB() #設置clf為高斯樸素貝葉斯分類器clf.fit(X, Y) #訓練數(shù)據(jù)print(clf.predict([[-1, 0]])) #預測數(shù)據(jù)[-1,0]屬于哪一類

輸出結(jié)果為: [1]。 這里面我們可以看到有 X,Y 兩個變量，X是我們要訓練的數(shù)據(jù)特征，而Y給的是對應數(shù)據(jù)的標簽，分成 [1],[2] 兩類。用 clf.fit 訓練好了之后，用 clf.predict 預測新數(shù)據(jù)[-1,0]，結(jié)果是被分為第一類，說明結(jié)果是令人滿意的。

MCMC(Markov chain Monte Carlo)

你以為說到這貝葉斯的事情就結(jié)束了？那你真的就是太 naive 了。貝葉斯公式里的 θ 只是一個參數(shù)，有沒有想過有兩個參數(shù)怎么辦？還能怎么辦，分布的積分改成雙重積分唄。可以可以，那如果有 3個、5個、10 個參數(shù)呢？還有十重積分嘛？很顯然積分這個工具只適合我們在一維和二維的情況下進行計算，三維以上的效果就已經(jīng)不好了；其實不僅僅在于多維情況，就算是在一維情況很多積分也很難用數(shù)值方法計算出來，那該怎么辦？于是便有了 MCMC 方法，全稱是馬爾科夫鏈蒙特卡洛方法。大家別指望在下文里看到詳細的計算過程和推導，我還是按照我的理解，簡單地從原理出發(fā)進行描述，讓大家有一個感性的認識。

第二個MC：蒙特卡洛方法

雖然蒙特卡洛方法是 MCMC 中的第二個 MC，但先解釋蒙特卡洛方法會更加容易理解。蒙特卡洛方法也稱蒙特卡洛抽樣方法，其基本思想是通過大量取樣來近似得到想要的答案。有一個經(jīng)典的試驗就是計算圓周率，在一個邊上為1的正方形中畫一個內(nèi)切圓，圓的面積就是 π，圓面積比上整體的正方形面積也是 ππ, 現(xiàn)在在正方形內(nèi)產(chǎn)生大量隨機數(shù)，最后我們只需要計算在圓內(nèi)點的個數(shù)比上總體點的個數(shù)，便近似得到了圓周率 π 的值(這些統(tǒng)計學家是真聰明啊。。。)。

現(xiàn)在回到貝葉斯公式，我們現(xiàn)在有一個后驗概率 π(θ|x) ，但我們其實最想知道的是 h(θ) 的后驗期望：

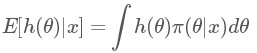
怎么又跑出來一個 h(θ) ？不要著急，如果我們令 h(θ)=θ , 那上面這個積分求得就是我們想要的后驗期望估計了！(當然 h(θ) 還可以是其他情況，會得到其他我們想要的結(jié)果，例如后驗最大估計，后驗方差等等，這里就不贅述了) 蒙特卡洛方法指出：如果我們可以從后驗概率分布 π(θ|x) 中抽取大量的獨立同分布(i.i.d)的觀測值 θ1,θ2,…,θm ,于是我們可以用如下公式：

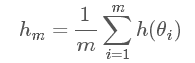
在大數(shù)定理的支持下，hm 就可看作是 E[h(θ)|x] 的近似值。但是這個方法在多維和后驗分布形式未知的情況下，很難抽樣，于是便有了第一個 MC，馬爾科夫鏈的方法。

第一個MC：馬爾科夫鏈

馬爾科夫鏈也稱之為馬氏鏈，先來看一下數(shù)學定義：

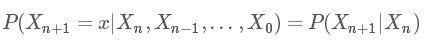
意思就是，從 Xn,Xn?1,…,X0 到 Xn+1 的轉(zhuǎn)移概率只與 Xn+1 的前一個狀態(tài) Xn 有關。

如果條件概率 P(Xn+1|Xn) 與 n 無關，成為一個固定值，那么就稱這個馬氏鏈有平穩(wěn)轉(zhuǎn)移概率，記為 pij 。并且我們稱 P=(pij) 為馬氏鏈的轉(zhuǎn)移矩陣，且滿足條件：

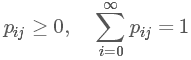
怎么一個概率變成一個矩陣了？？？其實這個轉(zhuǎn)移概率 pij 指的只是狀態(tài) i 中的一個觀測值 Xn 到狀態(tài) j 中的另一個觀測值 Xn+1 的概率，其實我們在每個狀態(tài)下許許多多的觀測值。我隨便舉一例子：

現(xiàn)有一個轉(zhuǎn)換矩陣：

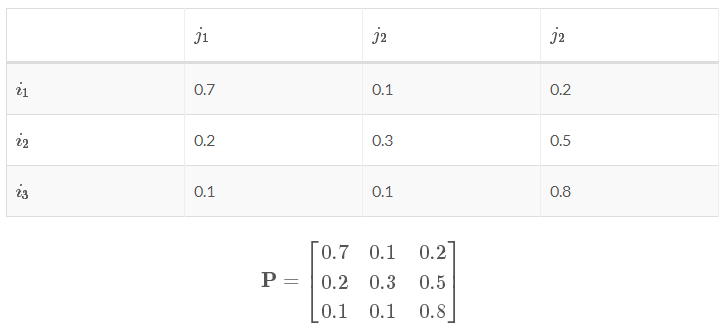
可以看出狀態(tài) i 中的一個觀測值轉(zhuǎn)移到下個狀態(tài) j 的分別三個觀測值的概率和為1。

下面就是最最重要的馬氏鏈的平穩(wěn)性(也可稱之為收斂性)：

設馬爾科夫鏈有轉(zhuǎn)移概率矩陣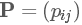, 一個概率分布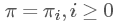如果滿足?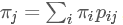則稱之為此馬爾科夫鏈的平穩(wěn)分布。（取自[1]中定義6.3.2）

可能這么看這個定義還是有點繞，這里的 i,j 并不是指從 i 一步就到了 j ,求和符號 ∑ 的意思就是能讓概率分布 π(i) 經(jīng)過 n 步之后成為平穩(wěn)分布 π(j) 。我們得到的平穩(wěn)分布 π(j)=[π(1),π(2),…,π(j)] 里面各個概率的和也為1。

現(xiàn)在我們就要把這個馬爾科夫鏈和貝葉斯聯(lián)系起來，按照我的理解，π(i) 就是我們的先驗分布，如果我們能找到一個轉(zhuǎn)移矩陣，那么我們就會在n步之后就會收斂到一個平穩(wěn)分布，而這個分布就是我們要的后驗分布。得到平穩(wěn)分布后，根據(jù)平穩(wěn)性，繼續(xù)乘上這個轉(zhuǎn)移概率矩陣，平穩(wěn)分布依然不會改變，所以我們就從得到平穩(wěn)分布開始每次對其中抽樣 1 個出來，再經(jīng)過 m 步之后，我們就得到了 m 個服從后驗分布的 i.i.d 樣本，便可按照第二個 MC 蒙特卡洛方法進行計算了！

當然，還有很多理論是關于如何找這個轉(zhuǎn)移概率矩陣的，和算法如何實現(xiàn)的，但這些都太復雜了，就不在這里說了。MCMC 是一個有著完整體系的東西，市面上都很少有詳細介紹其理論過程的資料，有的話那都不是幾十頁紙能講完的。有一些很好的講解可參考資料[1][4]，尤其是[4]是個很有名的文檔，講得非常通俗易懂、深入淺出，我在這兩個部分寫的少的原因就是如果寫多了也就是把這些資料對應部分重新說一遍，所以有興趣的就直接看這些資料吧。

MCMC 的 Python 實現(xiàn)——Pymc

原本想在這里詳細介紹一個例子的，但終究還是別人的例子，還是去看原資料比較好，見[4]。注意文件的文件是 ipython 的格式，用 anaconda 里的 Jupyter notebook 打開就行。還有要注意的是每個章節(jié)的內(nèi)容分為了pymc2 和 pymc3 兩個庫的實現(xiàn)。pymc3 需要依賴項 theano 才行，我一開始就一直運行不起來，原來 theano 只能在Python<3.6和scipy<0.17.1 才能運行。

結(jié)尾

這篇文章主要介紹了貝葉斯統(tǒng)計的數(shù)學思想，這篇文章從頭到尾寫了有近十個小時了，希望能對大家有所幫助，如果有任何錯誤和解釋不當?shù)牡胤剑埥o我評論，我也只是個初學者，也希望能得到大神的指點。