編者按：當初學者第一次接觸機器算法時，直觀了解算法正在做什么是一項非常重要的任務，這也是論智一直推崇可視化方法的原因之一。雖然初級算法的數學計算并不難掌握，但當他們一看到滿篇的數學理論和符號，學習下去的興致和氣勢就消減了不少。

作為一名數據工作者，這年頭“熟悉機器學習算法”遠比“精通Excel”在求職市場上要搶手得多，但前者的“熟悉”究竟是熟悉到什么程度呢？Excel本身就能編寫大量基礎機器學習算法，而且對于初學者來說，這樣的編寫過程不僅能加深對算法的理解，還能幫助他們更充分地感受算法的美妙。

下面我們用一個例子來證明這一點。

從本質上來說，大多數數據科學算法其實就是優化問題，而其中最常用的算法之一就是梯度下降算法。對于初學者來說，梯度下降這個詞可能乍一聽有些可怕，但它真的這么復雜嗎？

以下是一個房價預測任務：根據歷史房價數據創建一個模型，結合房屋面積預測新房價格。讓我們先用已有數據建立一個表格：

如上表所示，房屋面積是X，房價是Y，由此我們可以繪制歷史房價數據折線圖：

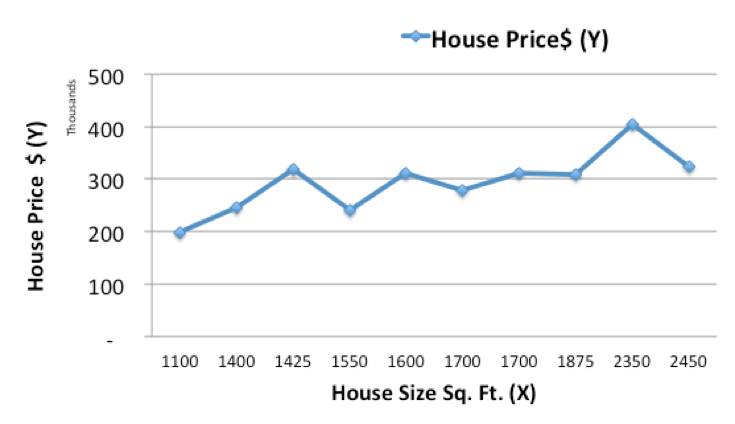
現在用一個簡單的線性模型，對歷史數據進行擬合，根據房屋面積X預測新房價格Y(pre)：

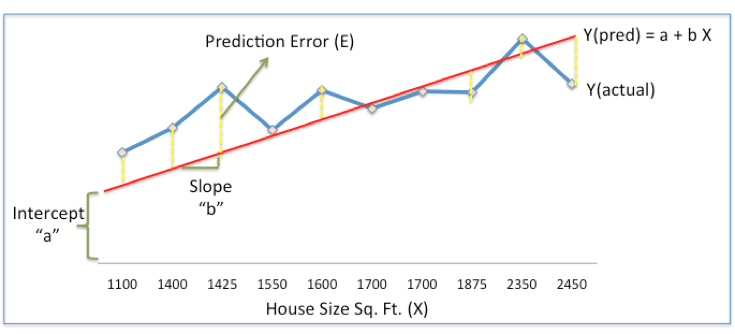
在上圖中，紅線是我們的線性模型，因此鑒于橫坐標和縱坐標信息，它的表達式是：Y(pred) = a + bX。

藍線是已知的歷史房價，從分布上簡單給出了房價和房屋面積相關程度的基本信息。

連接紅線和藍線的黃色虛線表示對于同一面積的房屋，模型預測和實際房價的誤差（E）。

所以我們的目標是找到最好的a和b，使誤差項E最小：

殘差平方和（SSE）= ?(真實房價-預測房價)2= ?(Y - Ypred)2

（SSE只是一種方法，還可以用其他方法統計誤差）

好了，下面我們就要用到梯度下降了。梯度下降是一種優化算法，它能幫我們找到優化權重(a,b)，并保證模型預測的準確率。下面是具體步驟：

步驟1：用隨機值初始化權重a和b，并計算誤差（SSE）。

步驟2：計算梯度，即當權重從初始隨機值逐漸變小時SSE的變化。這有助于我們把a和b朝SSE最小的方向優化。

步驟3：用梯度調整權重以使SSE最小化，以達到最佳值。

步驟4：用新權重進行預測，并計算新的SSE。

步驟5：重復步驟2和3，直到再次調整權重后不再明顯降低預測錯誤率。

如果說這樣描述有些泛泛而談，下面我們就結合圖表詳細介紹。請牢記一點，事先把數據處理好有助于更高效的優化。

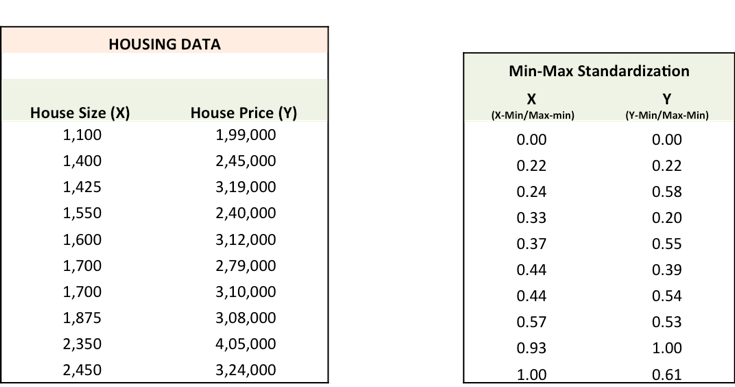
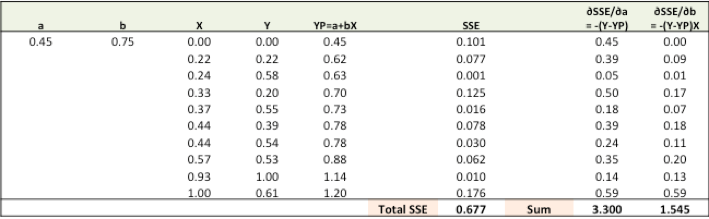
第一步： 為了擬合Y(pred) = a + bX，用隨機值初始化a和b，并計算預測誤差（SSE）。

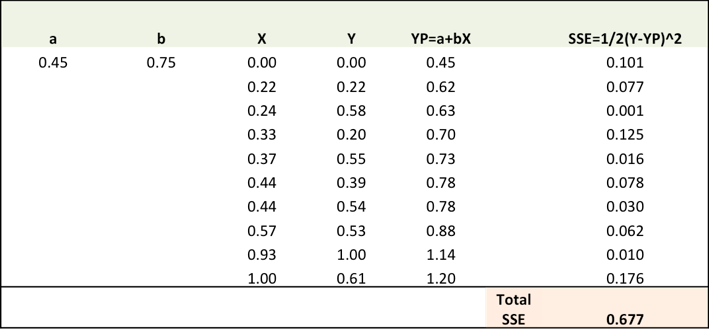
第二步：計算權重的誤差梯度。

?SSE/?a =-(Y-Ypred)

?SSE/?b =-(Y-Ypred)X

其中，SSE=? (Y-Ypred)2= ?(Y-(a+bX))2

雖然有一點點讓人煩惱的微積分計算，但這已經很基礎了，?SSE/?a和?SSE/?b是我們想要的梯度，它們給出了SSE“下降”的方向。

第三步：用梯度調整權重，使SSE獲得最小值，也就是最佳值。

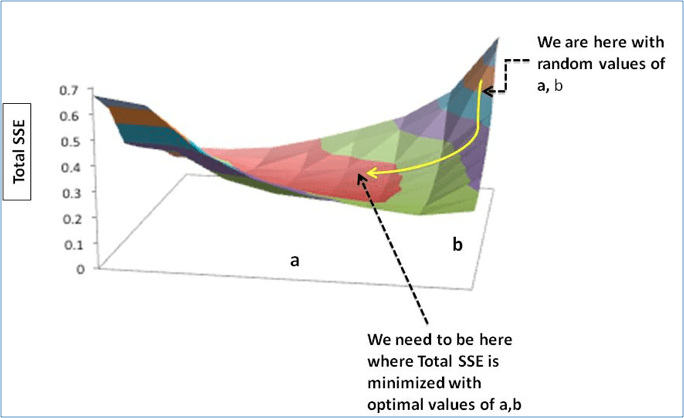
這之后我們就能用新權重更新a和b的值，以便模型沿著最優方向移動。

因為

a-?SSE/?a

b-?SSE/?b

所以更新規則就是：

新的a = a - r × ?SSE/?a = 0.45–0.01× 3.300 = 0.42

新的b = b - r × ?SSE/?b = 0.75–0.01×1.545 = 0.73

其中r=0.01是學習率，表示權重調整的步幅。

第四步：用新的a和b進行預測并計算新的SSE。

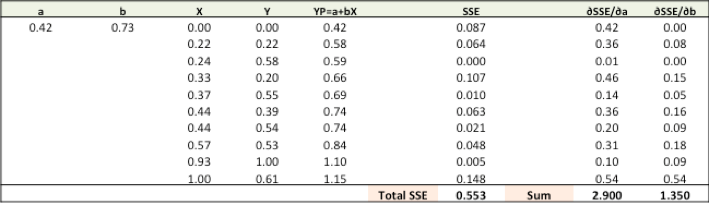
可以看到，SSE已經從0.677下降到0.553了，這意味著模型的預測準確率有所提高。

第五步：重復第二步和第三步，直到再改變a和b，SSE不再發生明顯變化。

以上就是用Excel實現的梯度下降算法，比起一堆數學計算，這樣圖文并茂的演示是不是更有趣呢？

在MOOC課程中，除了吳恩達的deeplearning.ai和Udacity，李飛飛強烈推薦的Fast.ai也有其獨到之處。這家公司的CEO Jeremy Howard是深度學習領域的一朵奇葩，他沒有過硬的學術背景，也沒有大型科技公司的就職經歷，僅憑自學就在kaggle競賽中鋒芒畢露。對于這樣一個人，他的課絕對值得初學者學習。