編者按:物理學(xué)碩士、深度學(xué)習(xí)開發(fā)者Artem Oppermann介紹了受限玻爾茲曼機(jī)的原理。近幾年來,隨著受限玻爾茲曼機(jī)在協(xié)同過濾上的大放異彩,這一基于能量的神經(jīng)網(wǎng)絡(luò)很受歡迎。
0. 導(dǎo)言
受限玻爾茲曼機(jī)(RBM)是一種屬于能量模型的神經(jīng)網(wǎng)絡(luò)。本文的讀者對受限玻爾茲曼機(jī)可能不像前饋神經(jīng)網(wǎng)絡(luò)或卷積神經(jīng)網(wǎng)絡(luò)那樣熟悉。然而,隨著RBM在Netflix Prize(知名的協(xié)同過濾算法挑戰(zhàn))上大放異彩(當(dāng)前最先進(jìn)的表現(xiàn),擊敗了大多數(shù)競爭者),最近幾年這類神經(jīng)網(wǎng)絡(luò)很受歡迎。
1. 受限玻爾茲曼機(jī)
1.1 架構(gòu)
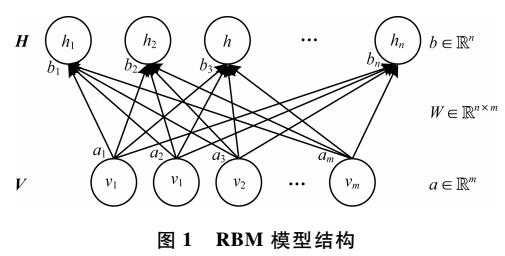
在我看來,RBM是所有神經(jīng)網(wǎng)絡(luò)中最簡單的架構(gòu)之一。如下圖所示,一個受限玻爾茲曼機(jī)包含一個輸入層(v1, ..., v6),一個隱藏層(h1, h2),以及相應(yīng)的偏置向量a、b. 顯然,RBM沒有輸出層。不過之后我們會看到,RBM不需要輸出層,因?yàn)镽BM進(jìn)行預(yù)測的方式和通常的前饋神經(jīng)網(wǎng)絡(luò)不同。
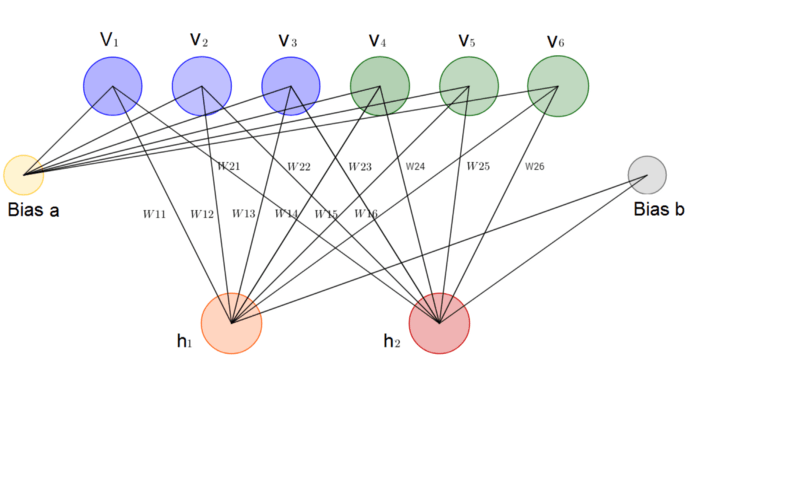
1.2 能量模型
乍看起來,能量這一術(shù)語和深度學(xué)習(xí)沒什么關(guān)系。相反,能量是一個物理概念,例如,重力勢能描述了具有質(zhì)量的物體因重力而具有的相對其他質(zhì)量體的潛在能量。不過,有些深度學(xué)習(xí)架構(gòu)使用能量來衡量模型的質(zhì)量。
深度學(xué)習(xí)模型的目的之一是編碼變量間的依賴關(guān)系。給變量的每種配置分配一個標(biāo)量作為能量,可以描述這一依賴關(guān)系。能量較高意味著變量配置的兼容性不好。能量模型總是嘗試最小化一個預(yù)先定義的能量函數(shù)。
RBM的能量函數(shù)定義為:
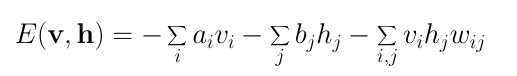
由定義可知,能量函數(shù)的值取決于變量/輸入狀態(tài)、隱藏狀態(tài)、權(quán)重和偏置的配置。RBM的訓(xùn)練包括為給定的輸入值尋找使能量達(dá)到最小值的參數(shù)。
1.3 概率模型
受限玻爾茲曼機(jī)是一個概率模型。這一模型并不分配離散值,而是分配概率。在每一時(shí)刻RBM位于一個特定的狀態(tài)。該狀態(tài)指輸入層v和隱藏層h的神經(jīng)元值。觀察到v和h的特定狀態(tài)的概率由以下聯(lián)合分布給出:
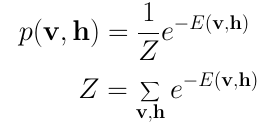
這里Z被稱為配分函數(shù)(partition function),該函數(shù)累加所有輸入向量和隱藏向量的可能組合。
這是受限玻爾茲曼機(jī)和物理學(xué)第二個相遇的地方。在物理學(xué)中,這一聯(lián)合分布稱為玻爾茲曼分布,它給出一個微粒能夠在能量E的狀態(tài)下被觀測到的概率。就像在物理中一樣,我們分配一個觀測到狀態(tài)v和h的概率,這一概率取決于整個模型的能量。不幸的是,由于配分函數(shù)Z中v和h所有可能的組合數(shù)目十分巨大,計(jì)算這一聯(lián)合分布十分困難。而給定狀態(tài)v計(jì)算狀態(tài)h的條件概率,以及給定狀態(tài)h計(jì)算狀態(tài)v的條件概率則要容易得多:
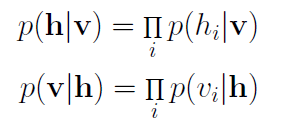
RBM中的每個神經(jīng)元只可能是二元狀態(tài)0或1中的一種。我們最關(guān)心的因子是隱藏層或輸入層地神經(jīng)元位于狀態(tài)1(激活)的概率。給定一個輸入向量v,單個隱藏神經(jīng)元j激活的概率為:
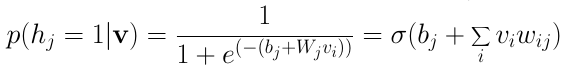
其中,σ為sigmoid函數(shù)。以上等式可由對之前的條件概率等式應(yīng)用貝葉斯定理推導(dǎo)得出,這里不詳細(xì)介紹其中的推導(dǎo)過程。
類似地,單個輸入神經(jīng)元i為1的概率為:
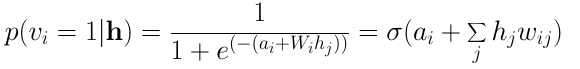
2. 基于受限玻爾茲曼機(jī)實(shí)現(xiàn)協(xié)同過濾
2.1 識別數(shù)據(jù)中的潛在因子
讓我們假定,我們找了一些人,讓他們給一批電影打分(一星到五星)。在經(jīng)典因子分析背景下,每部電影可以通過一組潛在因子來解釋。例如,《哈利波特》和《速度與激情》可能分別與奇幻、動作這兩個潛在因子有密切的關(guān)系。另一方面,喜歡《玩具總動員》和《機(jī)器人總動員》的用戶可能和皮克斯這個潛在因子密切相關(guān)。RBM可以用來分析和找出這些潛在因子。經(jīng)過一些epoch的訓(xùn)練,神經(jīng)網(wǎng)絡(luò)多次見到數(shù)據(jù)集中的每個用戶的所有評分。此時(shí)模型應(yīng)該已經(jīng)基于用戶的偏好和所有用戶的協(xié)同口味學(xué)習(xí)到了隱藏的潛在因子。
隱藏因子分析以二元的方式進(jìn)行。用戶并不向模型提交具體的評分(例如,一到五星),而是簡單地告知喜歡(評分為1)還是不喜歡(評分為0)某部特定的電影。二元評分值表示輸入層的輸入。給定這些輸入,RBM接著嘗試找出數(shù)據(jù)中可以解釋電影選擇的潛在因子。每個隱藏神經(jīng)元表示一個潛在因子。給定一個包含數(shù)以千計(jì)的電影的大規(guī)模數(shù)據(jù)集,我們相當(dāng)確定用戶僅僅觀看和評價(jià)了其中一小部分電影。另外,有必要給尚未評分的電影分配一個值,例如,-1.0,這樣在訓(xùn)練階段網(wǎng)絡(luò)可以識別未評分的電影,并忽略相應(yīng)的權(quán)重。
讓我們看一個例子。一個用戶喜歡《指環(huán)王》和《哈利波特》,但不喜歡《黑客帝國》、《搏擊俱樂部》、《泰坦尼克》。用戶還沒有看過《霍比特人》,所以相應(yīng)的評分為-1. 給定這些輸入,玻爾茲曼機(jī)可能識別出三個對應(yīng)電影類型的隱藏因子戲劇、奇幻、科幻。
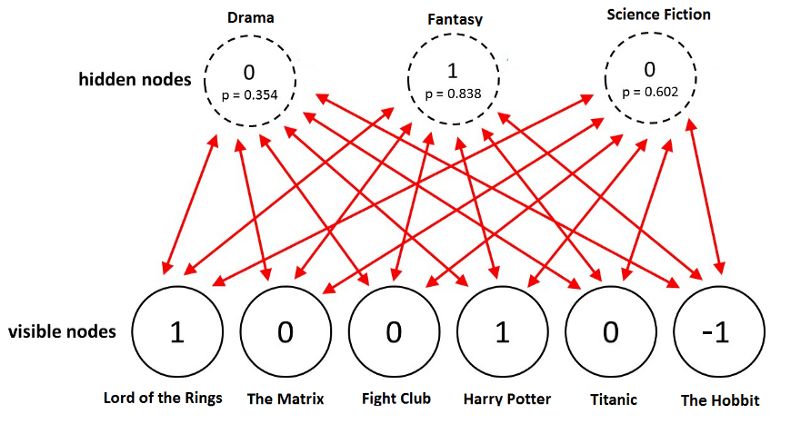
給定電影,RBM為每個隱藏神經(jīng)元分配一個概率p(h|v)。使用概率p從伯努利分布中取樣得到最終的神經(jīng)元的二元值。
在這個例子中,只有表示類型奇幻的隱藏神經(jīng)元被激活。給定這些電影評分,受限玻爾茲曼機(jī)能夠正確識別用戶最喜歡奇幻類型的電影。
2.2 將潛在因子用于預(yù)測
訓(xùn)練之后,我們的目標(biāo)是預(yù)測沒看過的電影的二元評分。給定特定用戶的訓(xùn)練數(shù)據(jù),網(wǎng)絡(luò)能夠基于用戶的偏好識別潛在因子。由于潛在因子由隱藏神經(jīng)元表示,我們可以使用p(v|h)從伯努利分布取樣,以找出哪個輸入神經(jīng)元處于激活狀態(tài)。
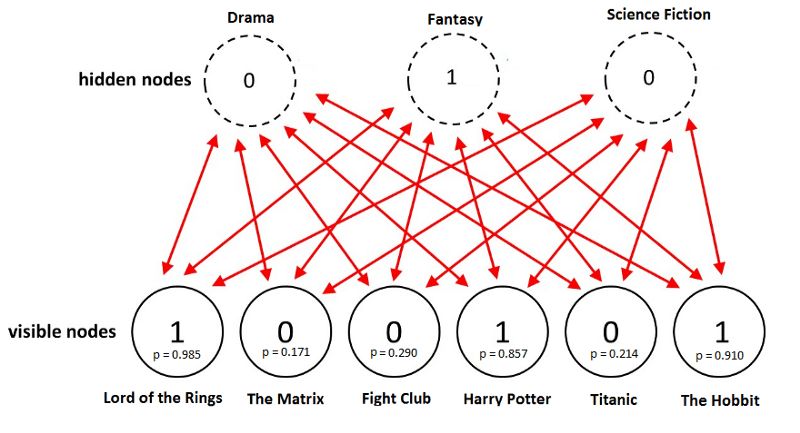
上圖中,網(wǎng)絡(luò)成功地識別出奇幻為用戶偏愛的電影類型,并預(yù)測用戶會喜歡《霍比特人》。
總結(jié)一下,從訓(xùn)練到預(yù)測的全過程如下:
基于所有用戶的數(shù)據(jù)訓(xùn)練網(wǎng)絡(luò)。
在推理時(shí)刻,獲取某個特定用戶的訓(xùn)練數(shù)據(jù)。
基于這一數(shù)據(jù)得出激活的隱藏神經(jīng)元。
基于隱藏神經(jīng)元的值得出激活的輸入神經(jīng)元。
輸入神經(jīng)元的新值顯示了用戶將對沒看過的電影作出的評價(jià)。
3. 訓(xùn)練
受限玻爾茲曼機(jī)的訓(xùn)練過程和基于梯度下降的常規(guī)神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程不同。本文不會詳細(xì)介紹具體的訓(xùn)練過程(感興趣的讀者可以閱讀受限玻爾茲曼機(jī)的原始論文),相反,我們將簡單地概覽一下其中的兩個主要的訓(xùn)練步驟。
3.1 吉布斯采樣
訓(xùn)練的第一個關(guān)鍵步驟稱為吉布斯采樣(Gibbs Sampling)。給定輸入向量v,我們使用前面提到的p(h|v)公式預(yù)測隱藏值h。得到了隱藏值之后,我們又使用前面提到的p(v|h)公式預(yù)測新輸入值v。這一過程輾轉(zhuǎn)重復(fù)k次。經(jīng)過k個迭代后,我們得到了輸入向量vk,這是基于原始輸入值v0的重建值。
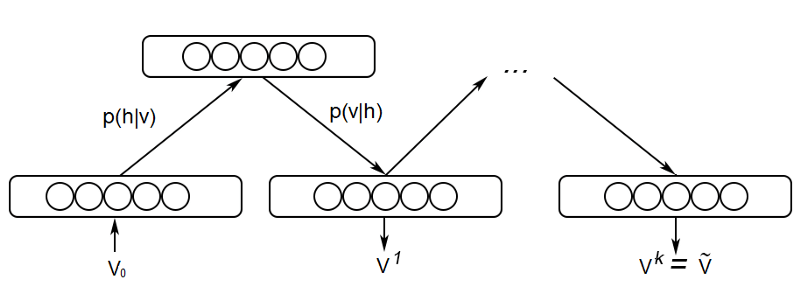
3.2 對比發(fā)散
在對比發(fā)散(Contrastive Divergence)這一步驟中,模型更新權(quán)重矩陣。使用向量v0和vk計(jì)算隱藏值h0和hk的激活概率。這些概率的外積和輸入向量v0、vk的差別為更新矩陣(update matrix):
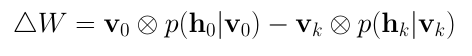
基于更新矩陣,使用梯度上升(gradient ascent)方法更新權(quán)重:

-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4779瀏覽量
101052 -
深度學(xué)習(xí)
+關(guān)注
關(guān)注
73文章
5512瀏覽量
121415
原文標(biāo)題:深度學(xué)習(xí)邂逅物理:受限玻爾茲曼機(jī)原理解析
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
一種基于能量模型的神經(jīng)網(wǎng)絡(luò)架構(gòu)受限玻爾茲曼機(jī)

用實(shí)驗(yàn)證明,二極管PN結(jié)中的玻爾茲曼常數(shù)
絕對干貨!HarmonyOS開發(fā)者日資料全公開,鴻蒙開發(fā)者都在看
HDC 2022 開發(fā)者主題演講與技術(shù)分論壇干貨分享(附課件)
稀疏受限玻爾茲曼機(jī)研究綜述
關(guān)于機(jī)器學(xué)習(xí)的15大框架分析
深度學(xué)習(xí)的機(jī)會網(wǎng)絡(luò)鏈路預(yù)測
融入受限玻爾茲曼機(jī)的偏最小二乘優(yōu)化方法
人工智能機(jī)器學(xué)習(xí)之受限玻爾茲曼機(jī)(RBM)算法
快速了解神經(jīng)網(wǎng)絡(luò)與深度學(xué)習(xí)的教程資料免費(fèi)下載




 深度學(xué)習(xí)開發(fā)者Artem Oppermann介紹了受限玻爾茲曼機(jī)的原理
深度學(xué)習(xí)開發(fā)者Artem Oppermann介紹了受限玻爾茲曼機(jī)的原理










評論