摘要:
極化碼是目前唯一可以從數(shù)學角度證明達到香農(nóng)極限的糾錯編碼技術。但是傳統(tǒng)的譯碼算法、連續(xù)刪除(SC)譯碼和連續(xù)刪除列表(SCL)譯碼算法復雜度較高,使得譯碼過程有較大譯碼延時。經(jīng)過研究譯碼算法的原理和特點,證明部分節(jié)點的譯碼運算是冗余,提出了SC譯碼和SCL譯碼簡化算法。證明了簡化的譯碼算法在保證譯碼性能不變的前提下,顯著降低了譯碼的復雜度。
0 引言
2009年ARIKAN E教授提出了極化碼[1],并且通過數(shù)學方法證明了當碼長無限長時其性能可以達到香農(nóng)極限。極化碼一經(jīng)提出就在國際上引起廣泛的關注,并且在2016年11月3GPP RAN1 #87會議上確定5G eMBB場景控制信道編碼為極化碼。
極化碼在實際應用中存在著一些缺點。連續(xù)刪除(Successive Cancellation,SC)譯碼對于長碼有很好的糾錯性能,但是對中短碼長譯碼性能有顯著的降低。為了克服這個問題,學者們提出了許多改進方法,如置信傳播(Belief Propagation,BP)譯碼算法[2]、線性規(guī)劃(Linear Programming,LP)譯碼算法[3]等。這些算法雖然可以提高一部分譯碼性能,但是譯碼算法的復雜度太大。一些算法針對SC算法進行了改進,文獻[4]提出了連續(xù)刪除列表(Successive Cancellation List,SCL)譯碼算法,特別是在冗余循環(huán)校驗(Cyclic Redundancy Check,CRC)輔助下的SCL的譯碼性能可以超過最大似然(Maximum Likelihood,ML)譯碼[5]。但同時SCL譯碼的復雜度也隨之增加。文獻[6]中提出的堆棧SC(SCStack,SCS)譯碼有和SCL譯碼相同的譯碼性能,此外SCS譯碼的時間復雜度遠低于SCL譯碼,并且在高的信噪比下可以降低搜索寬度L。
本文對SC譯碼和SCL譯碼進行了算法簡化,降低了算法的復雜度和時延。并且用數(shù)學證明的方法證明了簡化算法的可行性。
1 極化碼編碼
Polar Code是一種結(jié)構(gòu)性與迭代性極強的信道編碼技術,其設計核心理論是對信道的極化,信道極化過程主要包括兩部分[1]:信道聯(lián)合過程和信道分裂過程。
1.1 信道極化[1]
信道聯(lián)合:對已知的二進制離散無記憶信道W進行N次迭代復制WN:XN→YN,N=2n,并對復制所得信道進行遞推方式組合。WN和WN之間的轉(zhuǎn)移概率關系為:

圖1所示為在高斯信道下,碼長為N=4 096的信道極化仿真圖。根據(jù)仿真結(jié)果,可以看出部分信道的信道容量成兩極分化。據(jù)此可以選出I(W)→1的信道傳輸信息比特作為信息位,I(W)→0的信道傳輸固定比特作為凍結(jié)位。
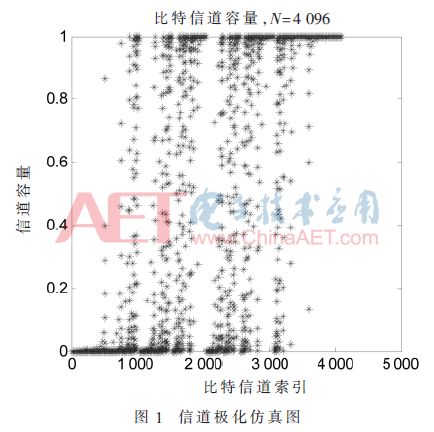
1.2 極化碼編碼


2 SC譯碼算法

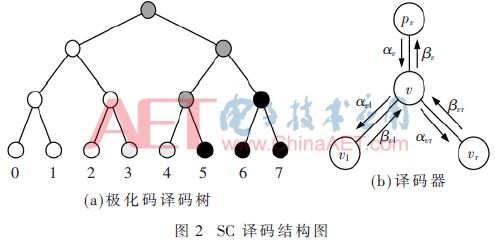


把βv傳遞給pv。這時v節(jié)點的譯碼消息傳遞終止,因為在余下譯碼過程中將不會再次激活節(jié)點v。
2.1 簡化的SC譯碼算法
本節(jié)通過簡化傳統(tǒng)譯碼的消息傳遞規(guī)則,簡化了SC譯碼算法。并且證明簡化譯碼算法的譯碼性能是與傳統(tǒng)的譯碼性能相同。
(1)Rate-0節(jié)點
對于Rate-0節(jié)點v,由于它所有后代都是Rate-0節(jié)點,因此當v接收到軟信息αv時,不去激活左右的子節(jié)點而直接計算βv:

對于任意dv=n-1的Rate-1節(jié)點一定滿足式(15)。假設dv=i的Rate-1節(jié)點也滿足(15),于是對于dv=i-1的Rate-1節(jié)點v的子節(jié)點dv=i,滿足式(15)。因此,根據(jù)上面的推導可以證明式(12)成立。
②證明式(13)成立:當dv=n時,對Rate-1節(jié)點,式(13)顯然是成立,因此,可以通過歸納法證明dv
2.2 算法復雜度分析
3 SCL譯碼算法
為了提高SC譯碼算法在碼長較短情況下糾錯能力,SCL譯碼算法被提出,L代表搜索寬度。每次必須有一點被估計,它的可能值0和1都需要被考慮。因為存在L組碼字候選,所以每次新的位估計產(chǎn)生2L組候選路徑,其中一半需要丟棄。因此,路徑度量值(Path Metric,PM)被提出。PM計算如下:
SCL譯碼算法是從根節(jié)點出發(fā),按廣度優(yōu)先的方法對路徑進行擴展;每一層向下一層擴展時,選擇當前層中具有較小PM的L條。當沒有到達葉節(jié)點而搜索寬度已經(jīng)達到,按照PM的從大到小的排列保留PM小的L條路徑。直到到達葉節(jié)點,然后選取PM最小路徑作為譯碼結(jié)果。
為了進一步提高極化碼的譯碼性能,編碼前在信息比特中添加CRC,然后利用SCL譯碼算法獲得L條搜索路徑,最后借助“正確信息比特可以通過CRC校驗”的先驗信息,對這L條搜索路徑進行挑選,從而得到正確譯碼結(jié)果。
4 簡化的SCL譯碼算法
傳統(tǒng)的SCL譯碼算法每次進行路徑擴展時都會產(chǎn)生2L條路徑,但是對于凍結(jié)比特,由于譯碼結(jié)果是已知的,因此對于凍結(jié)比特不進行路徑擴展,直接判決比特,路徑度量值也不改變,從而減少剪枝算法執(zhí)行的次數(shù),達到降低算法復雜度的目的。
由上述的譯碼過程分析,式(20)PM的計算可以改為:
因為凍結(jié)比特在譯碼過程中結(jié)果是已知的,所以不需要去選擇路徑,進而PM也不需要計算。另外,由于分裂次數(shù)的減少,剪枝算法也隨之減少,并最終達到了降低算法復雜度的目的。
5 仿真結(jié)果與分析
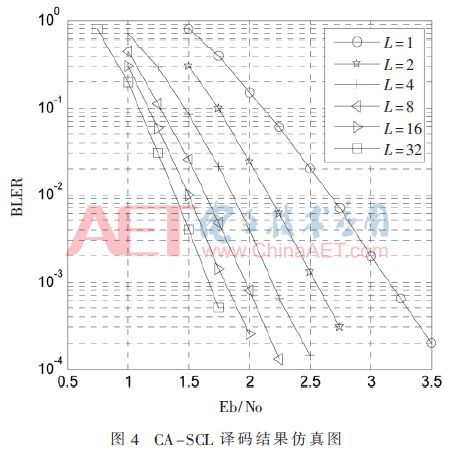
如圖4所示,在高斯信道下,碼長為1 024,碼率為0.5,采用二進制相移鍵控調(diào)制,譯碼輸出使用24位CRC校驗。搜索寬度L分別為1,2,4,8,16,32 的CA-SCL譯碼性能,仿真數(shù)據(jù)是106幀,一幀長1 024個比特。仿真結(jié)果表明,隨著L的值增加,誤碼率在逐漸降低,CA-SCL譯碼算法的性能明顯要優(yōu)于SC(L=1)譯碼算法。
6 結(jié)論
極化碼是目前唯一可以通過數(shù)學證明達到香農(nóng)極限的信道編碼技術,并且已經(jīng)成為5G控制信道的編碼方案。本文詳細敘述極化碼編譯碼的原理和結(jié)構(gòu),并提出關于SC譯碼和SCL譯碼的優(yōu)化算法,在不改變譯碼性能的前提下,降低了算法復雜度。通過對SC譯碼和SCL譯碼的性能進行了仿真分析,結(jié)果表明,隨著搜索寬度L的增加,極化碼的譯碼性更優(yōu),但復雜度也隨著增加。因此關于SCL的復雜度和數(shù)據(jù)吞吐量是下一步研究方向。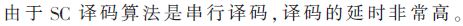



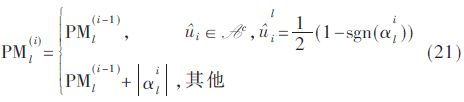
-
二進制
+關注
關注
2文章
795瀏覽量
41643 -
編碼技術
+關注
關注
1文章
35瀏覽量
11047 -
極化碼
+關注
關注
0文章
5瀏覽量
4168
原文標題:【學術論文】簡化的極化碼譯碼算法
文章出處:【微信號:ChinaAET,微信公眾號:電子技術應用ChinaAET】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
開關電源恒功率控制的輸入電壓補償方法
怎么設計一種基于C805lF020和Zigbee無線網(wǎng)絡的汽車測試系統(tǒng)?
電容器充電放電質(zhì)量變化實驗證明了愛因斯坦質(zhì)能公式E=mc2有
基于改進遺傳算法的路網(wǎng)路徑優(yōu)化方法
基于SOPC技術的PET瓶缺陷檢測系統(tǒng)設計
費馬大定理的證明
基于粒子群算法的波導縫隙天線的優(yōu)化設計

如何利用區(qū)塊鏈進行存在性證明?
難以證明又無法推翻的黎曼猜想被證明了嗎?
中科院以內(nèi)部討論組的形式做了關于證明黎曼猜想的報告
區(qū)塊鏈技術已經(jīng)從五個方面的應用領域中證明了其潛力
如何實現(xiàn)PBFT的數(shù)學證明
AI系統(tǒng)在外部驗證測試中證明了自己的才能
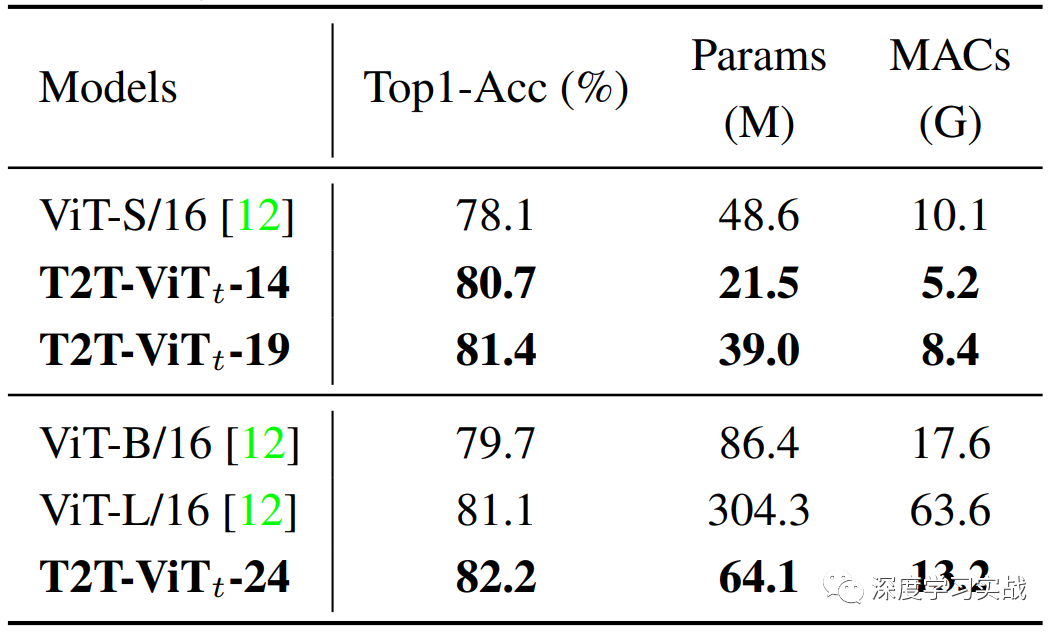
一種可以編碼局部信息的結(jié)構(gòu)T2T module,并證明了T2T的有效性




 用數(shù)學證明的方法證明了簡化算法的可行性
用數(shù)學證明的方法證明了簡化算法的可行性











評論