▌關于交叉熵在loss函數中使用的理解

交叉熵（cross entropy）是深度學習中常用的一個概念，一般用來求目標與預測值之間的差距。以前做一些分類問題的時候，沒有過多的注意，直接調用現成的庫，用起來也比較方便。最近開始研究起對抗生成網絡（GANs），用到了交叉熵，發現自己對交叉熵的理解有些模糊，不夠深入。遂花了幾天的時間從頭梳理了一下相關知識點，才算透徹的理解了，特地記錄下來，以便日后查閱。

信息論

交叉熵是信息論中的一個概念，要想了解交叉熵的本質，需要先從最基本的概念講起。

1 信息量

首先是信息量。假設我們聽到了兩件事，分別如下：

事件A：巴西隊進入了2018世界杯決賽圈。

事件B：中國隊進入了2018世界杯決賽圈。

僅憑直覺來說，顯而易見事件B的信息量比事件A的信息量要大。究其原因，是因為事件A發生的概率很大，事件B發生的概率很小。所以當越不可能的事件發生了，我們獲取到的信息量就越大。越可能發生的事件發生了，我們獲取到的信息量就越小。那么信息量應該和事件發生的概率有關。

假設X是一個離散型隨機變量，其取值集合為χ,概率分布函數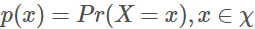，定義事件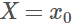的信息量為：

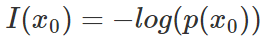
由于是概率所以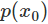的取值范圍是[0,1],繪制為圖形如下：?

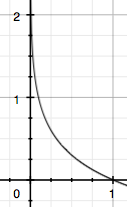
可見該函數符合我們對信息量的直覺

2 熵

考慮另一個問題，對于某個事件，有n種可能性，每一種可能性都有一個概率p(xi)。

這樣就可以計算出某一種可能性的信息量。舉一個例子，假設你拿出了你的電腦，按下開關，會有三種可能性，下表列出了每一種可能的概率及其對應的信息量

注：文中的對數均為自然對數

我們現在有了信息量的定義，而熵用來表示所有信息量的期望，即：

其中n代表所有的n種可能性，所以上面的問題結果就是

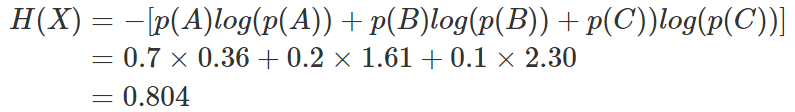
然而有一類比較特殊的問題，比如投擲硬幣只有兩種可能，字朝上或花朝上。買彩票只有兩種可能，中獎或不中獎。我們稱之為0-1分布問題（也叫二項分布），對于這類問題，熵的計算方法可以簡化為如下算式：

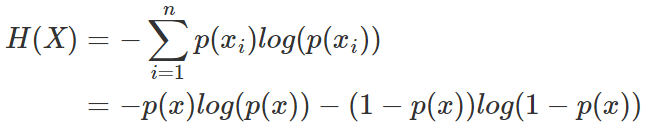
3 相對熵（KL散度）

相對熵又稱KL散度,如果我們對于同一個隨機變量 x 有兩個單獨的概率分布 P(x) 和 Q(x)，我們可以使用 KL 散度（Kullback-Leibler (KL) divergence）來衡量這兩個分布的差異

維基百科對相對熵的定義

In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P來描述目標問題，而不是用Q來描述目標問題，得到的信息增量。

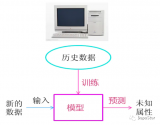
在機器學習中，P往往用來表示樣本的真實分布，比如[1,0,0]表示當前樣本屬于第一類。Q用來表示模型所預測的分布，比如[0.7,0.2,0.1]

直觀的理解就是如果用P來描述樣本，那么就非常完美。而用Q來描述樣本，雖然可以大致描述，但是不是那么的完美，信息量不足，需要額外的一些“信息增量”才能達到和P一樣完美的描述。如果我們的Q通過反復訓練，也能完美的描述樣本，那么就不再需要額外的“信息增量”，Q等價于P。

KL散度的計算公式：

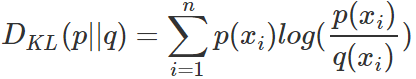
（3.1）

n為事件的所有可能性。

DKL的值越小，表示q分布和p分布越接近。

4 交叉熵

對式3.1變形可以得到：

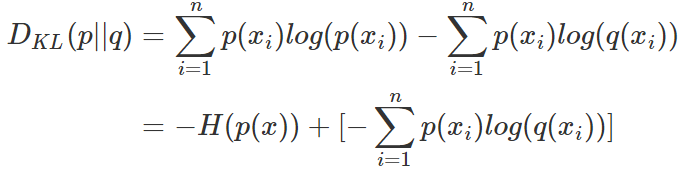
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

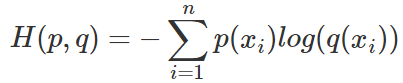
在機器學習中，我們需要評估label和predicts之間的差距，使用KL散度剛剛好，即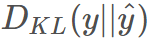，由于KL散度中的前一部分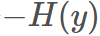不變，故在優化過程中，只需要關注交叉熵就可以了。所以一般在機器學習中直接用交叉熵做loss，評估模型。

▌機器學習中交叉熵的應用

1 為什么要用交叉熵做loss函數？

在邏輯回歸問題中，常常使用MSE（Mean Squared Error）作為loss函數，比如：

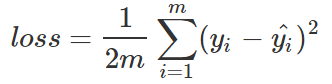
這里的m表示m個樣本的，loss為m個樣本的loss均值。

MSE在邏輯回歸問題中比較好用，那么在分類問題中還是如此么？

讓我們來看一下不同loss的函數曲線：

首先所有節點輸出都用的softmax

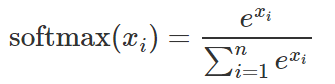
分別拿一個樣本來做示例，首先是使用MSE的loss

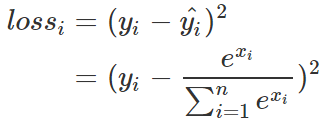
其中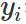和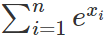都是常數，loss簡化為：?

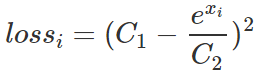
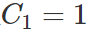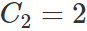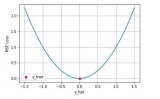
取,繪圖如下

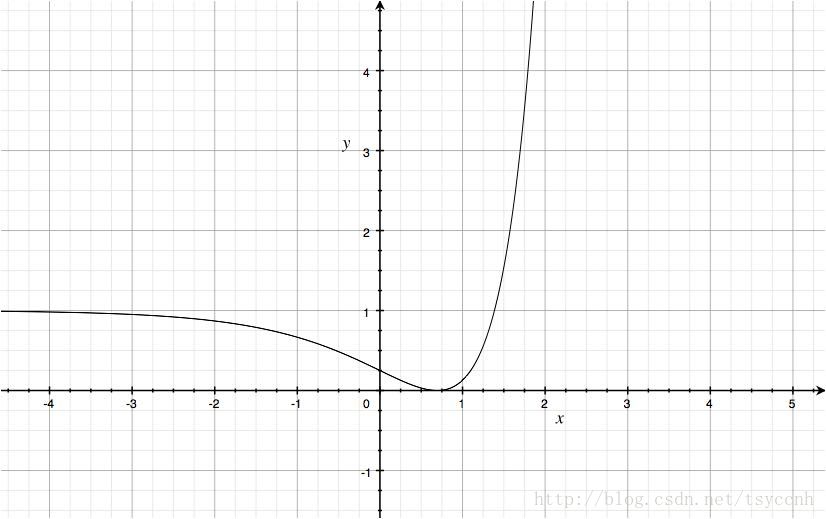
顯然，這個函數是非凸的，對優化問題來講，不太好優化，容易陷入局部極值點。

再來看使用交叉熵的loss

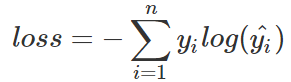
由于one-hot標簽的特殊性，一個1，剩下全是0，loss可以簡化為：

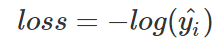
繪制曲線如下：

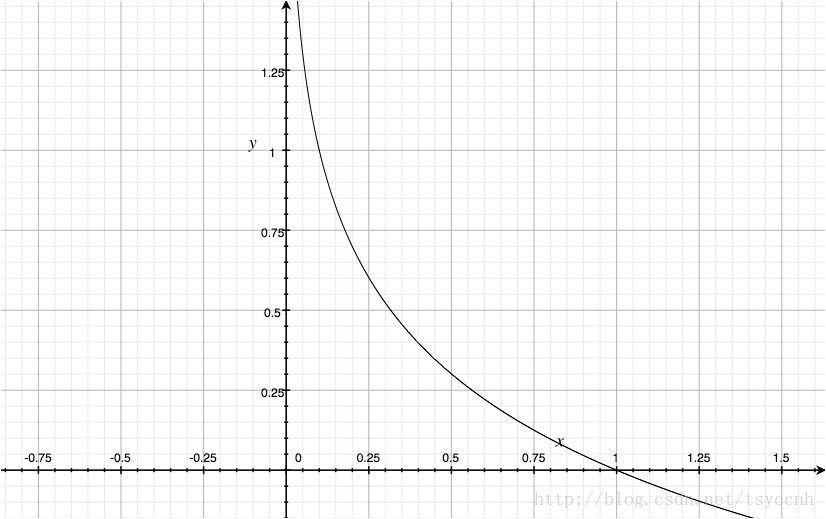
曲線是一個凸函數，自變量的取值范圍是[0,1]。凸函數便于梯度下降反向傳播，便于優化。所以一般針對分類問題采用交叉熵作為loss函數

2 交叉熵在單分類問題中的使用

這里的單類別是指，每一張圖像樣本只能有一個類別，比如只能是狗或只能是貓。

交叉熵在單分類問題上基本是標配的方法

上式為一張樣本的loss計算方法。式2.1中n代表著n種類別。

舉例說明,比如有如下樣本

對應的標簽和預測值

那么

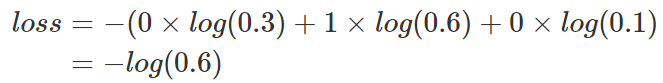
對應一個batch的loss就是

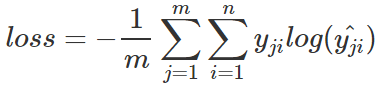
m為當前batch的樣本數

3 交叉熵在多分類問題中的使用

這里的多類別是指，每一張圖像樣本可以有多個類別，比如同時包含一只貓和一只狗。

和單分類問題的標簽不同，多分類的標簽是n-hot。

比如下面這張樣本圖，即有青蛙，又有老鼠，所以是一個多分類問題。

對應的標簽和預測值

值得注意的是，這里的Pred不再是通過softmax計算的了，這里采用的是sigmoid。將每一個節點的輸出歸一化到[0,1]之間。所有Pred值的和也不再為1。換句話說，就是每一個Label都是獨立分布的，相互之間沒有影響。所以交叉熵在這里是單獨對每一個節點進行計算，每一個節點只有兩種可能值，所以是一個二項分布。前面說過對于二項分布這種特殊的分布，熵的計算可以進行簡化。

同樣的，交叉熵的計算也可以簡化，即

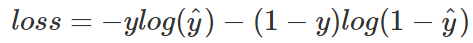
注意，上式只是針對一個節點的計算公式。這一點一定要和單分類loss區分開來。

例子中可以計算為：

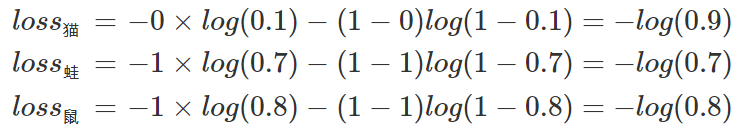
單張樣本的loss即為loss=loss貓+loss蛙+loss鼠

每一個batch的loss就是：

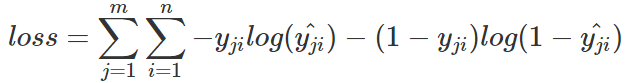
式中m為當前batch中的樣本量，n為類別數。

▌總結

路漫漫，要學的東西還有很多啊。