近日，加拿大猶太綜合醫(yī)院Lady Davis Institute的生物統(tǒng)計學(xué)家Alexia Jolicoeur-Martineau發(fā)表了一篇令人矚目的論文，引起“GAN之父”Ian Goodfellow的注意。在論文中，她指出現(xiàn)有的標(biāo)準(zhǔn)GAN（SGAN）還缺少一個基本屬性，即訓(xùn)練生成器時，我們不僅應(yīng)該提高偽數(shù)據(jù)是真實數(shù)據(jù)的概率，還應(yīng)該降低實際數(shù)據(jù)是真實數(shù)據(jù)的概率。這個屬性是一個重要基礎(chǔ)，它也是所有GAN都應(yīng)該遵守的。

在標(biāo)準(zhǔn)生成對抗網(wǎng)絡(luò)（SGAN）中，判別器負(fù)責(zé)估計輸入數(shù)據(jù)是真實數(shù)據(jù)的概率，根據(jù)這個數(shù)值，我們再訓(xùn)練生成器以提高偽數(shù)據(jù)是真實數(shù)據(jù)的概率。但本文認(rèn)為，判別器在提高“偽數(shù)據(jù)為真”的概率的同時，也應(yīng)該降低“實際數(shù)據(jù)為真”的概率，原因有三：

mini-batch中一半的數(shù)據(jù)是偽數(shù)據(jù)，這個先驗會帶來不合邏輯的結(jié)果；

在最小化散度（divergence minimization）的過程中，兩個概率不是同步變化；

實驗證實，經(jīng)過相對判別器誘導(dǎo)，SGAN的性能可以媲美基于IPM的GAN（WGAN、WGAN-GP等），而后者實際上已經(jīng)具有相對判別器的雛形，因此也更穩(wěn)定。

本文提出相對GAN（RGAN），并在它的基礎(chǔ)上又提出了一個變體——相對均值GAN（RaGAN），變體用平均估計計算判別器概率。此外，論文還顯示基于IPM的GAN其實是RGAN的子集。

通過比較，文章發(fā)現(xiàn)：(1)相比非相對GAN，RGAN和RaGAN更穩(wěn)定，產(chǎn)出的數(shù)據(jù)樣本質(zhì)量更高；(2)在RaGAN上加入梯度懲罰后，它能生成比WGAN-GP質(zhì)量更高的數(shù)據(jù)，同時訓(xùn)練時長僅為原先的1/5；(3)RaGAN能夠基于非常小的樣本（N = 2011）生成合理的高分辨率圖像（256x256），撇開做不到的GAN和LSGAN，這些圖像在質(zhì)量上也明顯優(yōu)于WGAN-GP和SGAN生成的歸一化圖像。

背景簡介

GAN是Ian Goodfellow等人在2014年提出的新型神經(jīng)網(wǎng)絡(luò)，它一經(jīng)面世就收獲大量關(guān)注，并在學(xué)界持續(xù)發(fā)酵。本文把最原始的GAN稱為標(biāo)準(zhǔn)GAN，也就是SGAN，它由一個生成器G和一個判別器D構(gòu)成，前者負(fù)責(zé)生成偽圖像，后者負(fù)責(zé)評估這個偽圖像是真實圖像的概率，然后輸出結(jié)果幫助生成器繼續(xù)訓(xùn)練，直到最后生成判別器都難辨真假的偽圖。

從計算角度看，GAN的生成器和判別器如下所示。其中f1,f2, g1, g2都是輸入標(biāo)量-輸出標(biāo)量的函數(shù)，P表示真實數(shù)據(jù)分布（xr實際數(shù)據(jù)），Q表示偽數(shù)據(jù)分布（xf偽數(shù)據(jù)），Pz是以0為中心的多元正態(tài)分布，方差為1，D(x)是判別器在x出的評估值。

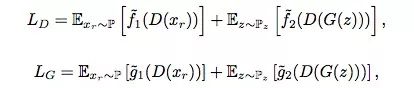
一般形式

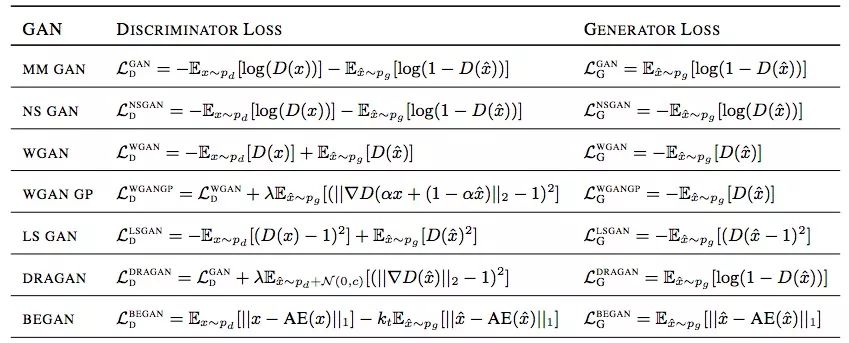
獨立形式：谷歌論文Are GANs Created Equal?

對于生成器，SGAN提出了兩種損失函數(shù)：saturating和non-saturating。其中前者不穩(wěn)定，后者較穩(wěn)定。如果GAN能100%分類真?zhèn)螖?shù)據(jù)，那saturating函數(shù)的梯度是0，non-saturating的梯度雖然不為0，但它是易變的（volatile）。這意味著如果學(xué)習(xí)率過高，判別器很可能會“放棄”學(xué)習(xí)，導(dǎo)致模型性能很差，這種現(xiàn)象在高維數(shù)據(jù)中尤為明顯。

雖然近幾年許多研究人員提出了很多新的損失函數(shù)，但它們相比SGAN沒有太多根本上的進(jìn)展，因此大多數(shù)GAN可以用non-saturating和saturating函數(shù)簡單地分成兩類：g1=? f1and g2=? f2，saturating；g1=f1and g2=f2，non-saturating。從本質(zhì)上來說，它們有一定的相通之處，為了后面方便對比，本文假設(shè)所有GAN都用non-saturating損失函數(shù)。

另外，一些研究人員發(fā)現(xiàn)把IPM（Integral probability metrics積分概率指標(biāo)）用于GAN可以大幅提高最終結(jié)果，但至于IPM為什么能得到這樣的效果，他們并沒有給出說明。而根據(jù)本文的研究，IPM GAN背后起作用的正是相對判別器。

SGAN遺漏的關(guān)鍵元素

本文論證的過程分為兩塊，一是直接分析“降低實際圖像是真實圖像概率”的必要性，二是用提出的RGAN和RaGAN和上述GAN做對比。本章是第一部分。

先驗知識

這塊內(nèi)容比較簡單。經(jīng)過足夠訓(xùn)練后，判別器如果性能過關(guān)，那它就應(yīng)該能正確區(qū)分大多數(shù)圖像的真?zhèn)涡裕褜嶋H圖像歸類為真實圖像，把偽圖像歸類為非真實圖像。而生成器的目標(biāo)是“愚弄”判別器，讓后者把更多的偽圖像分類為真實圖像，所以它會把一半實際圖像和一半偽圖像輸入判別器，期待從中學(xué)到更多真實圖像的分布。

雖然聽起來很有道理，但這是不合邏輯的。如果實際數(shù)據(jù)和偽數(shù)據(jù)看起來差不多，那大多數(shù)圖像的評估都符合C(xf) ≈ C(xr)。這時，如果判別器事先知道輸入圖像中一半真一半假，那它會認(rèn)為每張圖像為真的概率是0.5；如果判別器事先不知道，那它很可能就直接輸出D(x) ≈ 1。

如果生成器的學(xué)習(xí)率設(shè)得很高/迭代次數(shù)很多，再加上判別器輸出了個約等于1的概率，這時生成器“眼里”的實際數(shù)據(jù)和偽數(shù)據(jù)是不平等的，它會認(rèn)為偽數(shù)據(jù)更真實，C(xf) > C(xr)。而如果是堅信有一半偽數(shù)據(jù)的判別器，它會被迫把實際圖像分類成偽數(shù)據(jù)，背離正確分類的目標(biāo)。

最小化散度

在SGAN中，我們認(rèn)為判別器損失函數(shù)等于Jensen-Shannon散度（JSD）。因此，計算JSD可以等同為計算這個式子的最大值：

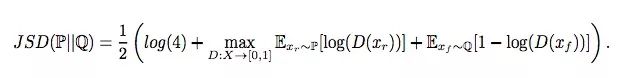
對于xr∈P和xf∈Q，如果D(xr) = D(xf) = 0.5，JSD最小化；如果D(xr) = 1，D(xf) = 0，JSD最大化。

如果我們想在JSD的最大值和最小值之間得出一個最小化的散度，這相當(dāng)于D(xr)的閾值是(0.5, 1)，D(xf)的閾值是(0, 0.5)。但如下圖所示，當(dāng)我們執(zhí)行最小化時，變化的只有D(xf)，而對實際圖像計算出的概率D(xr)卻沒有發(fā)生改變，這不合理。

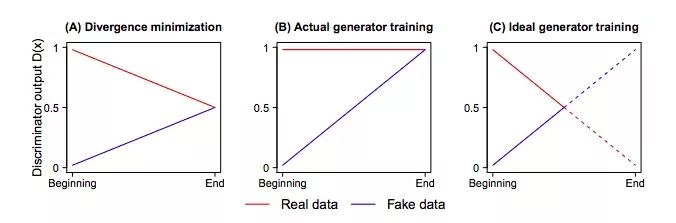
梯度

下面是SGAN和IPM GAN的損失函數(shù)對比：

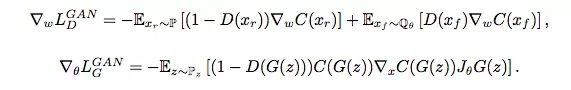
SGAN

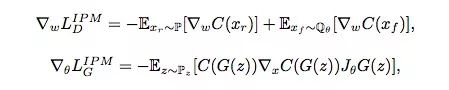
基于IPM的GAN

從這幾個方程可以看出，當(dāng)同時滿足以下幾點時，SGAN和 IPM GAN的結(jié)果是差不多的：

SGAN的判別器：D(xr) = 0，D(xf) = 1；

SGAN的生成器：D(xf) = 0；

C(x)∈F。

換句話說，如果生成器能直接影響判別器，那SGAN和基于IPM的GAN可以性能相近。對于后者，GAN在計算判別器損失函數(shù)梯度時會同時考慮實際數(shù)據(jù)和偽數(shù)據(jù)，但SGAN的D(xr)是不會隨著D(xf)變化而變化的，它會停止學(xué)習(xí)，轉(zhuǎn)而更關(guān)注偽數(shù)據(jù)。另一方面，如果D(xr)會隨D(xf)的上升而下降，這就意味著真實數(shù)據(jù)會被納入梯度計算中，這也是基于IPM的GAN更穩(wěn)定，而SGAN更容易崩潰的原因。

實驗對比

簡而言之，相對的GAN和普通GAN的區(qū)別如下所示。

標(biāo)準(zhǔn)GAN（SGAN）的判別器：

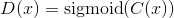
相對標(biāo)準(zhǔn)GAN（RSGAN）的判別器：

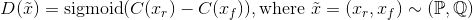
相對均值標(biāo)準(zhǔn)GAN（RaSGAN）的判別器：

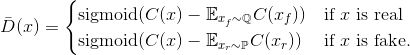
翻譯后的論文圖

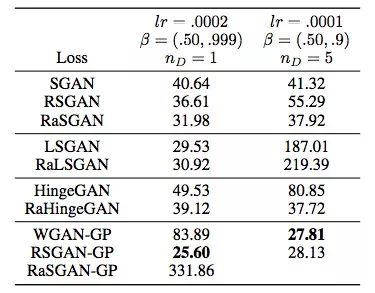
CIFAR-10上的FID值對比，RSGAN表現(xiàn)出眾

在LSGAN中引入相對判別器后生成的128×128貓圖，F(xiàn)ID值僅為15.85

WGAN-GP生成的256×256貓圖，F(xiàn)ID>100