非參數回歸(nonparametric regression)是一種在實踐中很有吸引力的方法,因為它非常靈活,對未知回歸函數的先驗結構假定限制相對寬松。然而,相應的代價是它需要大量標注數據,且隨著維度的增加而指數級增長——所謂維度的詛咒(curse of dimensionality)。標注數據極為耗時耗力,而在很多場景下,序信息(ordinal information)的獲取則相對而言成本較低。有鑒于此,CMU的研究人員Yichong Xu等提出了一種半監督算法排序回歸(Ranking-Regression),結合少量標注樣本,加上大量未標注樣本的序信息,逃脫維度的詛咒。
非參數方法
在監督學習問題中,我們有一些標注過的數據(觀測),然后尋找一個能夠較好地擬合這些數據的函數。
給定一些數據點,尋找擬合這些數據點的函數,我們首先想到的就是線性回歸:
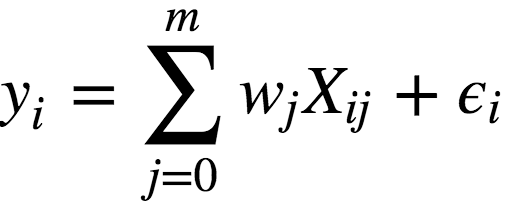
其中:
y為因變量(即目標變量);
w為模型的參數;
X為觀測及其特征矩陣;
?為對應于隨機、不可預測的模型錯誤的變量。
我們可以看到,線性回歸的過程,其實就是找出能夠最好地擬合觀測的參數w,因此,線性回歸屬于參數方法。
然而,線性回歸假定線性模型可以很好地擬合數據,這一假定未必成立。很多數據之間的關系是非線性的,而且很難用線性關系逼近。在這種情況下,我們需要用其他模型才能較好地擬合數據,比如,多項式回歸。
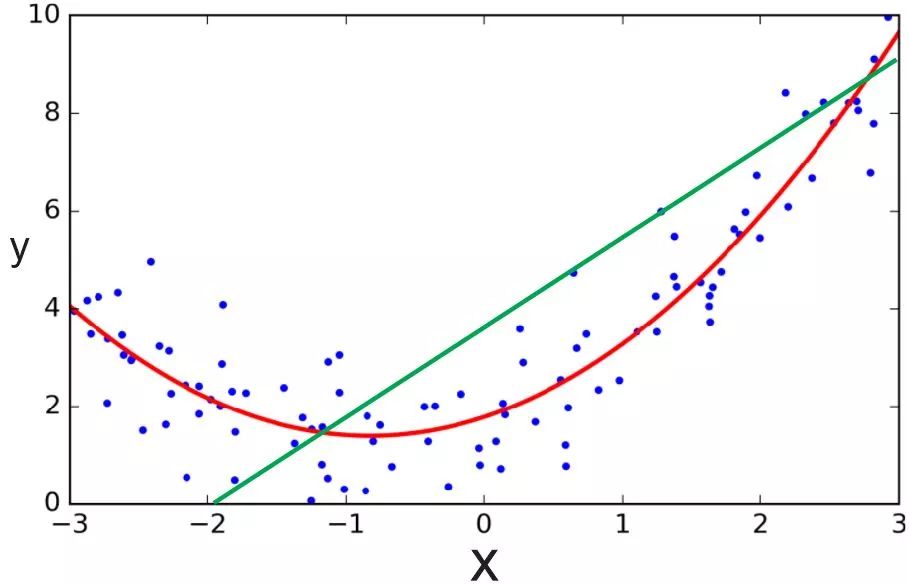
綠線為線性回歸,紅線為多項式回歸;圖片來源:ardianumam.wordpress.com
無論是線性回歸,還是多項式回歸,預先都對模型的結構有比較強的假定,例如數據可以通過線性函數或多項式函數來擬合,而這些假定不一定成立。因此,許多場景下,我們需要使用非參數回歸,也就是說,我們不僅需要找到回歸函數的參數,還需要找到回歸函數的結構。
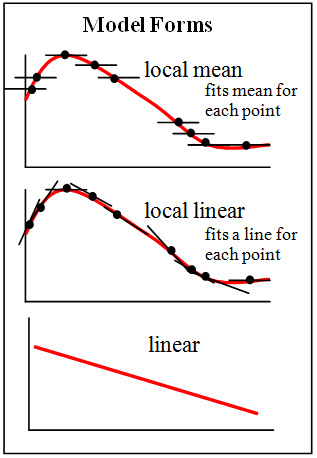
圖片來源:Brmccune;許可: CC BY-SA 3.0
例如,通常用于分類的K近鄰算法,其實還可以用于回歸。用于回歸的K近鄰算法,其基本流程和一般的用于分類的K近鄰算法差不多,唯一的區別是,分類時,目標變量的分類為它的最近鄰中最常見的分類(眾數),而回歸時,目標變量的值為它的最近鄰的均值(或中位數)。用于回歸的K近鄰算法,就是一種非參數回歸方法。
當然,非參數方法的靈活性不是沒有代價的。由于不僅回歸函數的參數未知,回歸函數的結構也未知,相比參數方法,我們需要更多的標注數據來訓練,以得到較好的結果。而隨著維度的增加,我們需要的標注數據的數量呈指數級增長。這也正是我們前面提到的維度的詛咒。前面我們舉了K近鄰作為非線性回歸的例子,而K近鄰正因受維度詛咒限制而出名。
有鑒于此,許多研究致力于通過給非參數回歸增加結構上的限制來緩解這一問題,例如,稀疏性或流形的限制(很多時候,高維數據空間是稀疏的,有時高維數據甚至基本上處于一個低維流形之上)。這是一件很有意思的事情。在實踐中,之所以選用非參數回歸,正是看重其靈活性,對擬合函數的結構沒有很強的假定。然而,當非參數回歸遇到維度詛咒的時候,我們又退回一步,通過加強結構上的假定來緩解維度詛咒問題。
而CMU的研究人員Yichong Xu、Hariank Muthakana、Sivaraman Balakrishnan、Aarti Singh、 Artur Dubrawski則采用了另外的做法,使用具有序信息的較大數據集補充帶標注的較小數據集,緩解非參數回歸在高維度下的問題。這一做法在實踐中意義很大,因為相對標簽而言,序信息的收集成本要低很多。例如,在臨床上,精確地評估單個患者的健康狀況可能比較困難,但是比較兩個患者誰更健康,則比較容易,也比較精確。
排序回歸算法
研究人員提出的排序回歸(Ranking-Regression)算法(以下簡稱R2),其基本直覺是根據序信息推斷未標注數據點的值。具體而言,根據序信息排序數據點,之后應用保序回歸(isotonic regression),然后根據已標注數據點和序信息推斷未標注數據點的值。經過以上過程之后,就可以用最近鄰算法估計新數據點的值了。
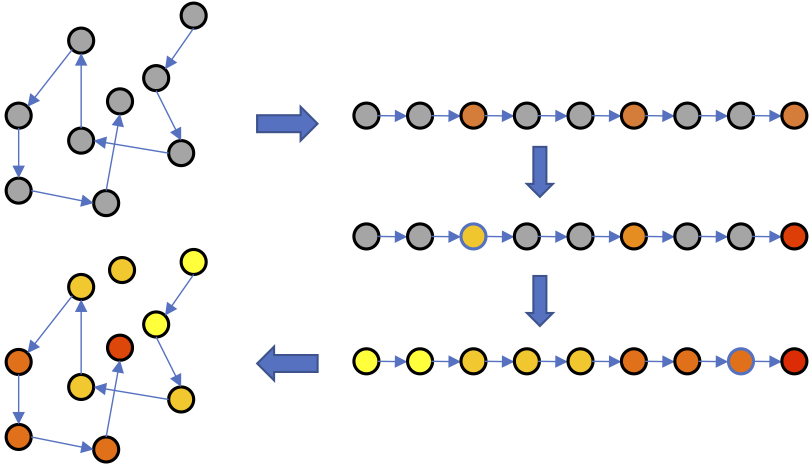
算法示意圖
上為R2算法示意圖。當然,如果你更習慣看偽代碼的話:

R2的上下界
顯然,用序信息代替標簽,有以次充好之嫌。因此,研究人員研究了R2算法的誤差上下界。
正如之前提到的,非參數回歸對結構的假定比較寬松,但也并不是毫無限制的。研究人員采用了經典的非參數回歸限制:
未標簽數據集{X1, ..., Xn}中,Xi∈ X ? [0,1]d,且Xi均勻獨立抽取自分布Px。而Px滿足其密度p(x)對x ∈ [0,1]d而言是有界的,即 0 < pmin?<= p(x) <= pmax。
回歸函數f同樣也是有界的([-M, M]),并且是赫爾德連續的,在0 < s <= 1時,
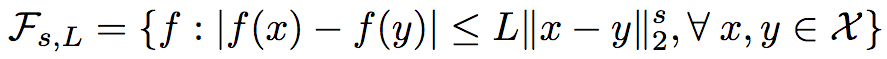
在滿足以上條件的條件下,研究人員證明了R2得出的回歸函數的均方誤差上界為:
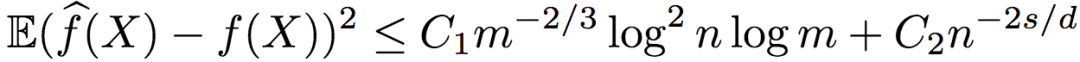
其中,C1、C2為大于0的常數。
而回歸函數的均方誤差下界為:
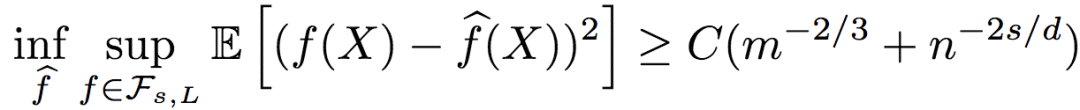
其中,C為大于0的常數。
由誤差上下界可知,基于序信息的排序回歸效果不錯,從對數因子上來說是最優的。
另外,從R2誤差的上界來看,只有序信息(n)依賴于維度d(不等式右側第二項),而標注信息并不依賴維度d(不等式右側第一項),也就是說,R2逃脫了維度的詛咒。
限于篇幅,這里就不介紹了證明過程了。上下界的證明思路,分別見論文的3.1小節和3.2小節;詳細證明過程,分別見論文的附錄B、C。
含噪聲的序信息
雖然之前說過序信息相對容易取得,也比較容易保持精確,但實際數據難免會有噪聲——錯誤的序信息。之前的結論都是在序信息不含噪聲的前提下得出的,那么,當序信息有噪聲的時候,情況又是怎么樣的呢?
研究人員進一步推導了序信息包含噪聲的情況。當然,噪聲是控制在一定范圍之內的。假定根據含噪序信息所得到的排序與真實排序之間的Kendall-Tau距離不超過vn2(n代表只有序信息的未標注數據),則R2的均方誤差的上界為:
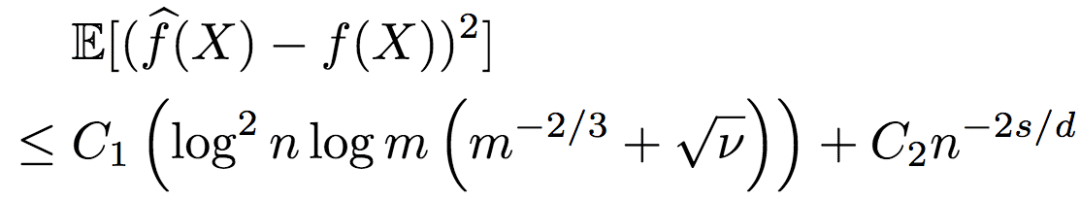
下界為:
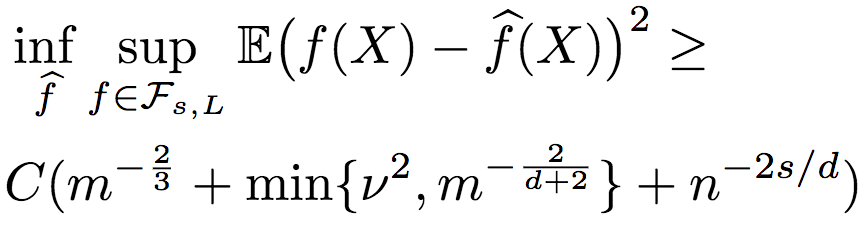
由此可知,R2的魯棒性相當好。當有足夠的序信息時,即使序信息包含一些噪聲,標注數據仍然不依賴于維度,也就是說,R2仍能逃脫維度的詛咒。
同樣,我們這里不給出具體的證明過程。請參考論文4.1、4.2小節了解證明思路,論文附錄D、F了解詳細證明過程。
另外,研究人員還進一步證明了(證明過程見附錄E),存在逼近函數f滿足
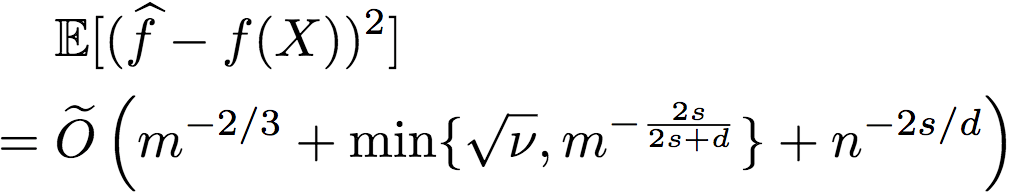
這就意味著,當噪聲過大(v過大)時,通過使用交叉驗證過程(R2和忽略序信息的簡單非參數回歸器),我們可以選擇較好的回歸方法,從而取得較優的表現。事實上,當我們有足夠標簽時,即使序信息非常噪雜,以上比率仍能收斂至0.
含噪聲的成對比較
有的時候,序信息是以成對比較(pairwise comparison)(數據點兩兩之間的大小)的形式取得的。當不含噪聲的時候,成對比較和之前提到的標準排序形式是等價的。但有噪聲的情況卻有所不同。研究人員證明了,在序信息為含噪聲的成對比較時,逼近函數的均方誤差的上界為:
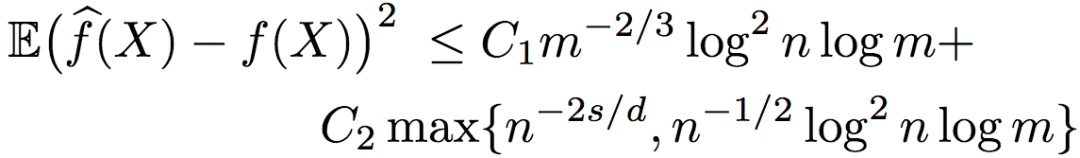
其中,C1和C2為大于0的常數。
由上式可知,當維度d >= 4s時,誤差取決于n-2s/d,并且,在這一設定下,基于含噪聲的成對比較的排序回歸,同樣從對數因子上來說是最優的。
試驗
為了驗證理論結果以及測試R2的實際表現,研究人員進行了一些試驗:
在模擬數據上進行試驗,這樣可以充分控制噪聲
在UCI數據集上進行試驗,通過標簽模擬排序
試驗R2在實際應用中的表現
在所有試驗中,研究人員對比了R2和K近鄰算法的表現。之所以選擇K近鄰,是因為K近鄰在理論上接近最優,并在實踐中應用廣泛。理論上說,有m個標注樣本時,k的最優值為m2/(d+2)。然而,對研究人員考慮的所有m、d值而言,m2/(d+2)非常小(< 5)。因此,研究人員的試驗中選用的是一組常量k值(不隨m改變)。每個試驗重復了20次,并對均方誤差取平均值。
模擬數據
研究人員采用如下方法生成了數據:令d = 8,均勻取樣X自[0, 1]d。目標函數為:
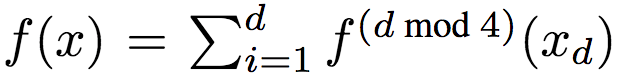
其中,xd為x的第d維,且
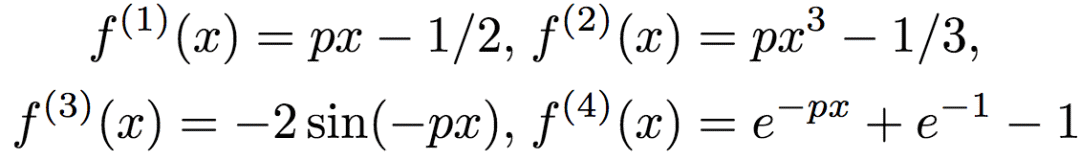
其中,p隨機均勻取樣自[0, 10]。研究人員調整了f(x),使其均值為0,方差為單位方差。通過y = f(x) + ε,ε ~ N(0, 0.52)生成標簽。
研究人員為訓練集和測試集各生成了1000個樣本。
研究人員測試了R2的兩個變體,1-NN和5-NN,在算法的最后一步分別使用1、5個最近鄰。5-NN并不影響之前理論分析部分的上下界,然而,從經驗出發,研究人員發現5-NN提升了表現。
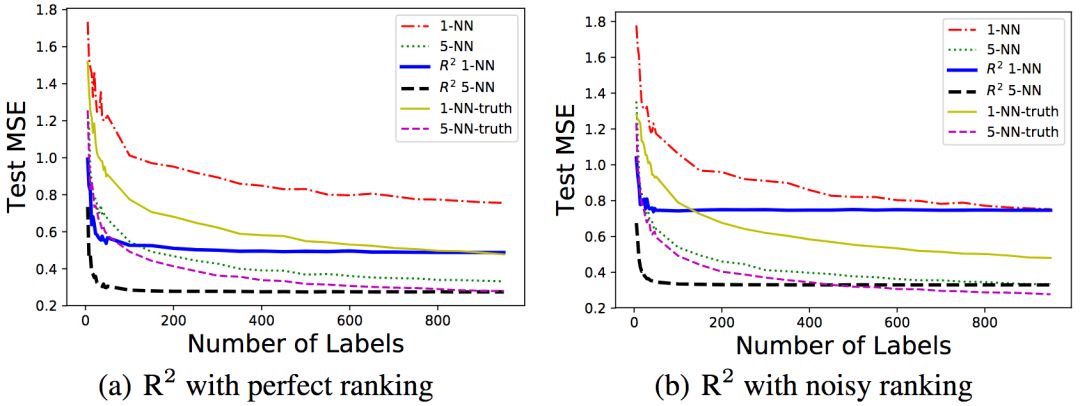
左:序信息無噪聲;右:序信息有噪聲
從上圖可以看到,無論序信息是否有噪聲,R2的表現都很好。
為了研究序信息噪聲的影響,研究人員在固定標注/排序樣本數100/1000的情況下,改變了序信息噪聲的等級。對噪聲水平σ,序信息通過y' = f(x) + ε'生成,其中ε' ~ N(0, σ2)。
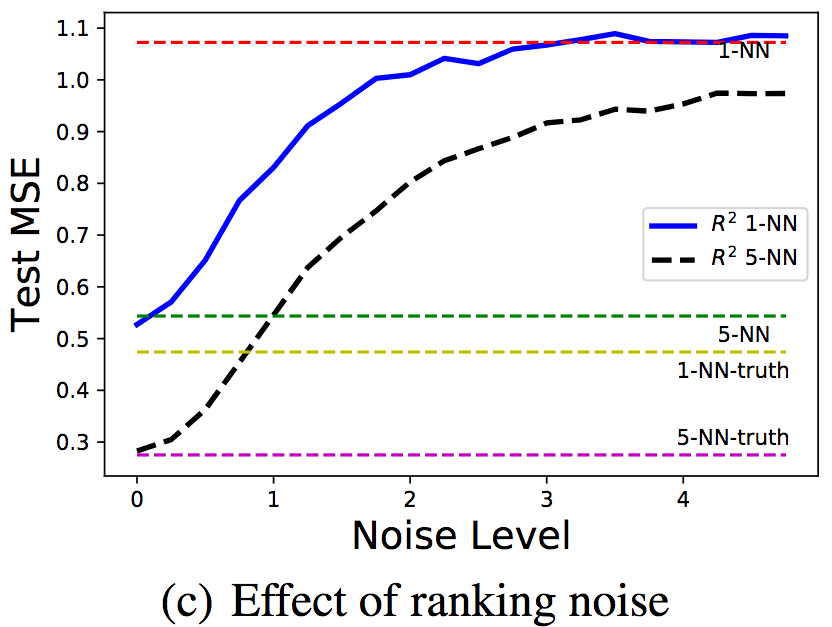
可以看到,隨著噪聲水平的升高,均方誤差也相應升高了。
UCI數據集
研究人員在兩個UCI回歸數據集上進行了試驗。這兩個數據集分別為Boston-Housing(波士頓房價)和diabetes(糖尿病)。序信息是通過數據集標簽生成的。
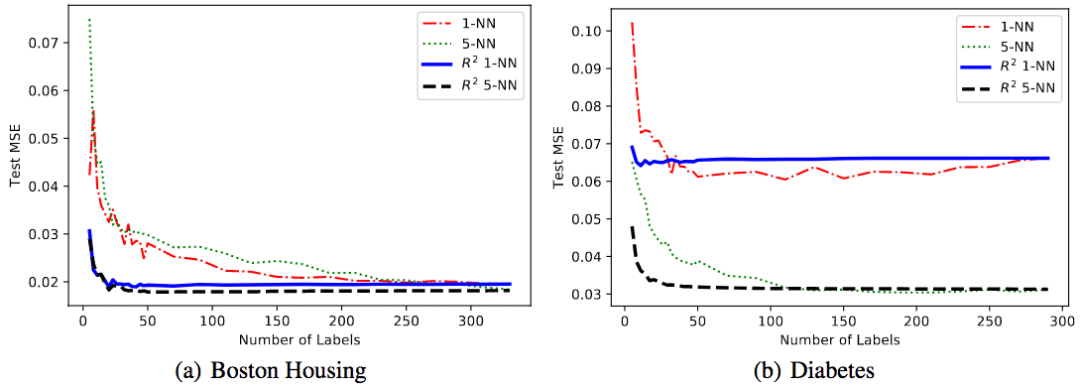
可以看到,相比不使用序信息的基線,R2在兩個數據集上的表現都更好。
根據肖像預測年齡
為了進一步在實踐中驗證R2算法,研究人員考慮了根據肖像估計人員年齡的任務。
研究人員使用了APPA-REAL數據集,該數據集包含7591張圖像,每張圖像都有相應的生物學年齡和表觀年齡。生物學年齡為實際年齡,表觀年齡基于眾包收集。根據多人的估計的平均值得到表觀年齡(平均有38個不同的估計者)。APPA-REAL同時提供了表觀年齡估計的標準差。數據集分為三部分,4113張訓練圖像、1500張驗證圖像、1978張測試圖像,研究人員的試驗只使用了訓練和驗證樣本。
研究人員使用FaceNet的最后一層從每張圖像中提取了128個維度的特征,并縮放每項特征使每個樣本X ∈ [0, 1]d。研究人員使用了5-NN和10-NN。除了像之前的試驗一樣,使用不包含序信息的5-NN、10-NN作為基線外,還比較了核支持向量回歸(SVR)的表現。SVR的參數配置為scikit-learn的標準配置,懲罰參數C = 1,RBF核,tolerance值為0.1.
研究人員試驗了兩個任務:
第一個任務的目標是預測生物學年齡。標簽為生物學年齡,而序信息基于表觀年齡生成。這是為了模擬現實場景,有一小部分樣本的真實年齡信息,但希望通過眾包的方式收集更多樣本的年齡信息。而在眾包時,讓人對樣本的長幼進行排序,要比直接估計年齡要容易一點,也精確一點。
第二個任務的目標是預測表觀年齡。在這一任務中,標簽和排序根據APPA-REAL提供的標準差生成。具體而言,標簽取樣自一個高斯分布,其均值等于表觀年齡,標準差為數據集提供的標準差。排序的生成分兩步,首先根據同樣的分布生成標簽,然后根據標簽排序。這是為了模擬現實場景中,讓人同時估計樣本的年齡,并對樣本的長幼進行排序。注意,在真實應用中,相比試驗,排序的噪聲會低一點。
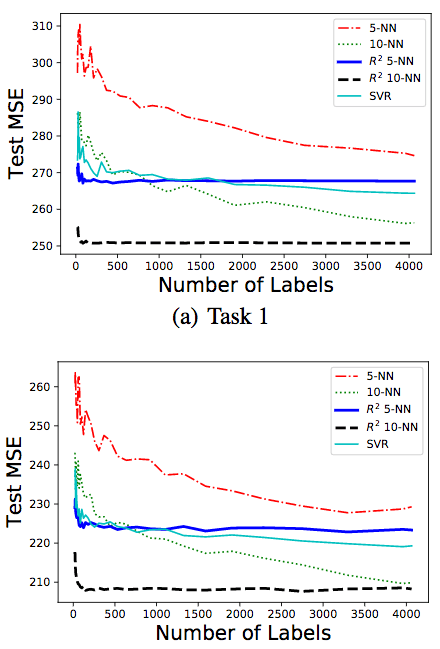
結果如上圖所示。我們可以看到,10-NN版本的R2的表現最好。而當樣本數少于500時,R2的10-NN版本和5-NN版本均優于其他算法。
結語
論文可通過預印本文庫獲取:arXiv:1806.03286
另外,本文作者將在ICML 2018上做口頭報告(Wed Jul 11th 11:00 -- 11:20 AM @ A6)。
-
函數
+關注
關注
3文章
4327瀏覽量
62573 -
線性
+關注
關注
0文章
198瀏覽量
25145 -
線性回歸
+關注
關注
0文章
41瀏覽量
4306
原文標題:排序回歸:基于序信息擺脫非參數回歸的維度詛咒
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
半監督典型相關分析算法
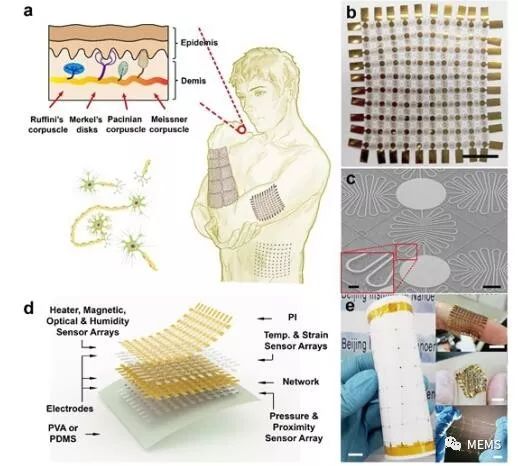
以色列研究人員開發出了一種能夠識別不同刺激的新型傳感系統
研究人員們提出了一系列新的點云處理模塊

研究人員推出了一種新的基于深度學習的策略
一種基于光滑表示的半監督分類算法

一種基于DE和ELM的半監督分類方法





 CMU的研究人員Yichong Xu等提出了一種半監督算法排序回歸
CMU的研究人員Yichong Xu等提出了一種半監督算法排序回歸












評論