函數逼近是機器學習中許多問題的核心，DeepMind的最新研究結合了神經網絡和隨機過程的優點，提出神經過程模型，在多任務上實現了很好的性能和高計算效率。

函數逼近（Function approximation）是機器學習中許多問題的核心，在過去十年來，這個問題的一種非常流行的方法是深度神經網絡。高級神經網絡由黑盒函數逼近器構成，它們學習從大量訓練數據點參數化單個函數。因此，網絡的大部分工作負載都落在訓練階段，而評估和測試階段則被簡化為快速的前向傳播。雖然高的測試時間性能對于許多實際應用是有價值的，但是在訓練之后就無法更新網絡的輸出，這可能是我們不希望的。例如，元學習（Meta-learning）是一個越來越受歡迎的研究領域，解決的正是這種局限性。

作為神經網絡的一種替代方案，還可以對隨機過程進行推理以執行函數回歸。這種方法最常見的實例是高斯過程（ Gaussian process, GP）,這是一種具有互補性質的神經網絡模型：GP不需要昂貴的訓練階段，可以根據某些觀察結果對潛在的ground truth函數進行推斷，這使得它們在測試時非常靈活。

此外，GP在未觀察到的位置表示無限多不同的函數，因此，在給定一些觀察結果的基礎上，它能捕獲其預測的不確定性。但是，GP在計算上是昂貴的：原始GP對數據點數量是3次方量級的scale，而當前最優的逼近方法是二次逼近。此外，可用的kernel通常以其函數形式受到限制，需要一個額外的優化過程來為任何給定的任務確定最合適的kernel及其超參數。

因此，將神經網絡和隨機過程推理結合起來，彌補兩種方法分別具有的一些缺點，這作為一種潛在解決方案越來越受到關注。在這項工作中，DeepMind研究科學家Marta Garnelo等人的團隊提出一種基于神經網絡并學習隨機過程逼近的方法，他們稱之為神經過程（Neural Processes, NPs）。NP具有GP的一些基本屬性，即它們學習在函數之上建模分布，能夠根據上下文的觀察估計其預測的不確定性，并將一些工作從訓練轉移到測試時間，以實現模型的靈活性。

更重要的是，NP以一種計算效率非常高的方式生成預測。給定n個上下文點和m個目標點，一個經過訓練的NP的推理對應于一個深度神經網絡的前向傳遞，它以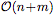scale，而不是像經典GP那樣以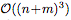。此外，該模型通過直接從數據中學習隱式內核（implicit kernel）來克服許多函數設計上的限制。

本研究的主要貢獻是：

提出神經過程（Neural Processes），這是一種結合了神經網絡和隨機過程的優點的模型。

我們將神經過程（NP）與元學習（meta-learning）、深層潛變量模型（deep latent variable models）和高斯過程（Gaussian processes）的相關工作進行了比較。鑒于NP與這些領域多有相關，它們讓許多相關主題之間可以進行比較。

我們通過將NP應用于一系列任務，包括一維回歸、真實的圖像補完、貝葉斯優化和contextual bandits來證明了NP的優點和能力。

神經過程模型

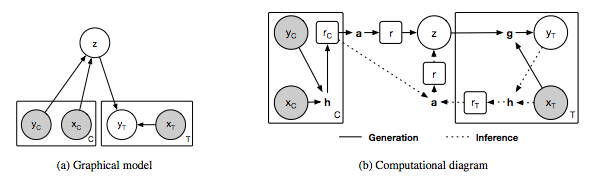
圖1：神經過程模型。

（a）neural process的圖模型，x和y分別對應于y = f(x)的數據，C和T分別表示上下文點和目標點的個數，z表示全局潛變量。灰色背景表示觀察到變量。

（b）neural process的實現示意圖。圓圈中的變量對應于(a)中圖模型的變量，方框中的變量表示NP的中間表示，粗體字母表示以下計算模塊：h - encoder, a - aggregator和g - decoder。在我們的實現中，h和g對應于神經網絡，a對應于均值函數。實線表示生成過程，虛線表示推理過程。

在我們的NP實現中，我們提供了兩個額外的需求：上下文點的順序和計算效率的不變性（invariance）。

最終的模型可歸結為以下三個核心組件（見圖1b）：

從輸入空間到表示空間的編碼器（encoder）h，輸入是成對的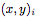上下文值，并為每對生成一個表示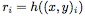。我們把h參數化為一個神經網絡。

聚合器（aggregator）a，匯總編碼器的輸入。

條件解碼器（conditional decoder）g，它將采樣的全局潛變量z以及新的目標位置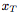作為輸入，并為對應的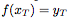的值輸出預測。

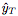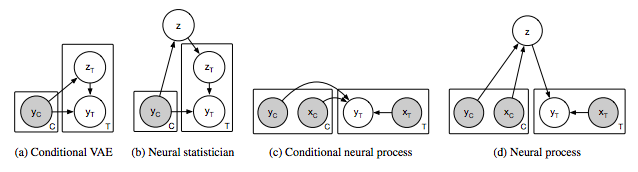
圖2：相關模型(a-c)和神經過程(d)的圖模型。灰色陰影表示觀察到變量。C表示上下文變量，T表示目標變量，即給定C時要預測的變量。

結果

圖4. MNIST和CelebA上的像素化回歸

左邊的圖展示了一張圖像完成像素化可以框定為一個2-D回歸任務，其中f(像素坐標)=像素亮度。右邊的圖展示了圖像實現MNIST和CelebA的結果。頂部的圖像對應提供給模型的上下文節點。為了能夠更清晰的展現，未被觀察到的點在MNIST和CelebA中分別標記為藍色和白色。在給定文本節點的情況下，每一行對應一個不同的樣本。隨著文本節點的增加，預測像素越來越接近底層像素，且樣本間的方差逐漸減小。

圖5. 用神經過程對1-D目標函數進行湯普森抽樣

這些圖展示了5次迭代優化的過程。每個預測函數（藍色）是通過對一個潛變量（latent variable）的采樣來繪制的，其中該變量的條件是增加文本節點（黑色）的數量。底層的ground truth函數被表示為一條黑色虛線。紅色三角形表示下一個評估點（evaluation point），它對應于抽取的NP曲線的最小值。下一個迭代中的紅色圓圈對應于這個評估點，它的底層ground truth指將作為NP的一個新文本節點。

表1. 使用湯普森抽樣對貝葉斯優化

優化步驟的平均數需要達到高斯過程生成的1-D函數的全局最小值。這些值是通過隨機搜索采取步驟數來標準化的。使用恰當的核（kernel）的高斯過程的性能等同于性能的上限。

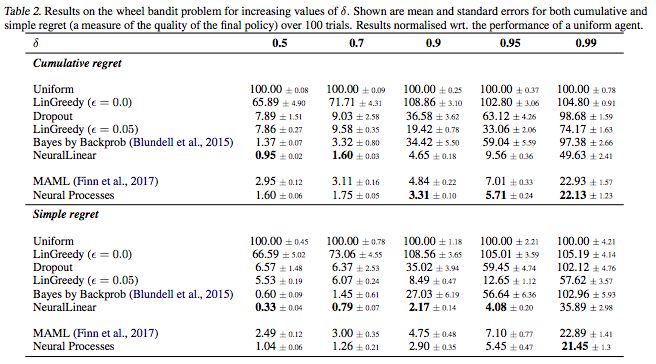
表2. 增加δ值后wheel bandit問題的結果

結果表示的是超過100次的累加regret和簡單regret的平均誤差和標準誤差。結果歸一化了一個統一體（uniform agent）的性能。

討論

我們介紹了一組結合隨機過程和神經網絡優點的模型，叫做神經過程。NPs學會在函數上表示分布，并且測試時根據一些文本輸入做出靈活的預測。NPs不需要親自編寫內核，而是直接從數據中學習隱式度量（implicit measure）。

我們將NPs應用于一些列回歸任務，以展示它們的靈活性。本文的目的是介紹NPs，并將它與目前正在進行的研究做對比。因此，我們呈現的任務是雖然種類很多，但是維數相對較低。將NPs擴展到更高的維度，可能會大幅度降低計算復雜度和數據驅動表示（data driven representations）。