▌引子
最近開始拾起來看一些 NLP 相關的東西,特別是深度學習在 NLP 上的應用,發現采樣方法在很多模型中應用得很多,因為訓練的時候如果預測目標是一個詞,直接的 softmax 計算量會根據單詞數量的增長而增長。恰好想到最開始深度學習在 DBN 的時候采樣也發揮了關鍵的作用,而自己對采樣相關的方法了解不算太多,所以去學習記錄一下,經典的統計的方法確實巧妙,看起來非常有收獲。
本篇文章先主要介紹一下經典的采樣方法如 Inverse Sampling、Rejective Sampling 以及 Importance Sampling 和它在 NLP 上的應用,后面還會有一篇來嘗試介紹 MCMC 這一組狂炫酷拽的算法。才疏學淺,行文若有誤望指正。
▌Why Sampling
采樣是生活和機器學習算法中都會經常用到的技術,一般來說采樣的目的是評估一個函數在某個分布上的期望值,也就是
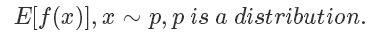
比如我們都學過的拋硬幣,期望它的結果是符合一個伯努利分布的,定義正面的概率為 p ,反面概率為 1-p 。最簡單地使 f(x)=x,在現實中我們就會通過不斷地進行拋硬幣這個動作,來評估這個概率p。
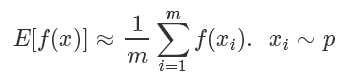
這個方法也叫做蒙特卡洛法(Monte Carlo Method),常用于計算一些非常復雜無法直接求解的函數期望。
對于拋硬幣這個例子來說:
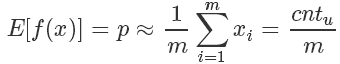
其期望就是拋到正面的計數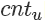 除以總次數 m。?
除以總次數 m。?
而我們拋硬幣的這個過程其實就是采樣,如果要用程序模擬上面這個過程也很簡單,因為伯努利分布的樣本很容易生成:
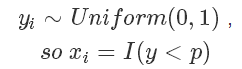
而在計算機中的隨機函數一般就是生成 0 到 1 的均勻分布隨機數。
▌Sampling Method
可以看到蒙特卡洛法其實就是按一定的概率分布中獲取大量樣本,用于計算函數在樣本的概率分布上的期望。其中最關鍵的一個步驟就是如何按照指定的概率分布 p 進行樣本采樣,拋硬幣這個 case 里伯努利分布是一個離散的概率分布,它的概率分布一般用概率質量函數(pmf)表示,相對來說比較簡單,而對于連續概率分布我們需要考慮它的概率密度函數(pdf):
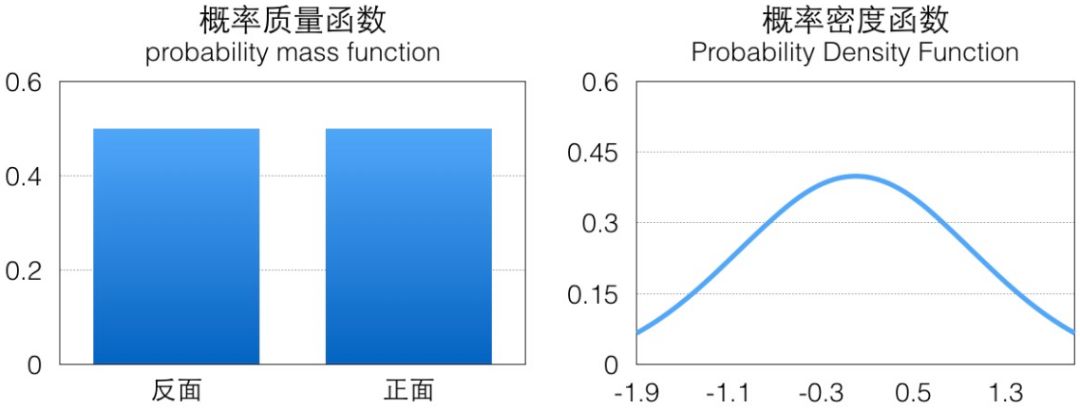
比如上圖示例分別是標準正態分布概率密度函數,它們的面積都是 1(這是概率的定義),如果我們可以按照相應概率分布生成很多樣本,那這些樣本繪制出來的直方圖應該跟概率密度函數是一致的。
而在實際的問題中,p 的概率密度函數可能會比較復雜,我們由淺入深,看看如何采樣方法如何獲得服從指定概率分布的樣本。
▌Inverse Sampling
對于一些特殊的概率分布函數,比如指數分布:
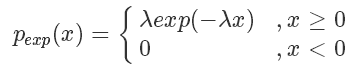
我們可以定義它的概率累積函數(Cumulative distribution function),也就是(ps.這個’F’和前面的’f’函數并沒有關系)
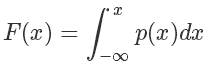
從圖像上看就是概率密度函數小于 x 部分的面積。這個函數在 x≥0 的部分是一個單調遞增的函數(在定義域上單調非減),定義域和值域是[0,+∞)→[0,1),畫出來大概是這樣子的一個函數,在 p(x) 大的地方它增長快(梯度大),反之亦然:
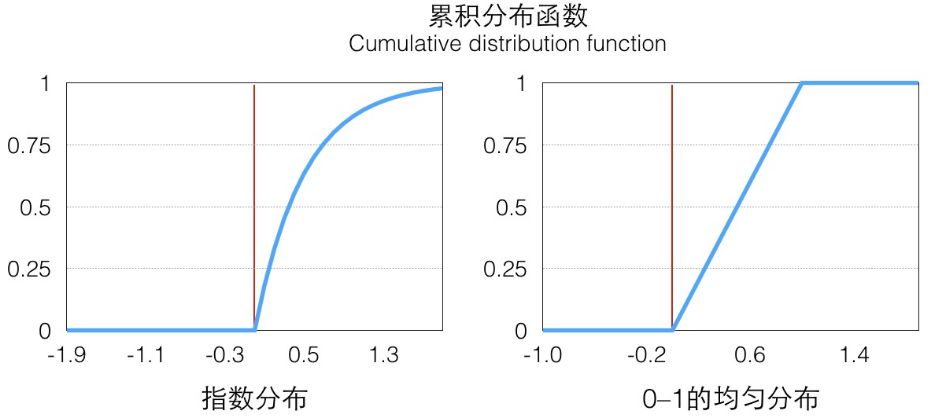
因為它是唯一映射的(在>0的部分,接下來我們只考慮這一部分),所以它的反函數可以表示為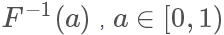 ,值域為[0,+∞)
,值域為[0,+∞)
因為F單調遞增,所以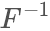 也是單調遞增的:?
也是單調遞增的:?
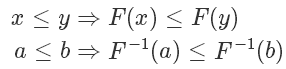
利用反函數的定義,我們有:
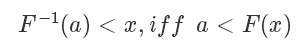
我們定義一下 [0,1] 均勻分布的 CDF,這個很好理解:
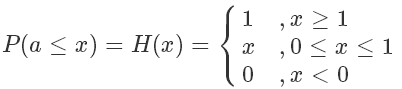
所以
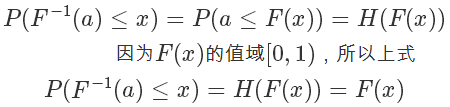
根據 F(x) 的定義,它是 exp 分布的概率累積函數,所以上面這個公式的意思是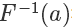 符合 exp 分布,我們通過 F 的反函數將一個 0 到 1 均勻分布的隨機數轉換成了符合 exp 分布的隨機數,注意,以上推導對于 cdf 可逆的分布都是一樣的,對于 exp 來說,它的反函數的形式是:?
符合 exp 分布,我們通過 F 的反函數將一個 0 到 1 均勻分布的隨機數轉換成了符合 exp 分布的隨機數,注意,以上推導對于 cdf 可逆的分布都是一樣的,對于 exp 來說,它的反函數的形式是:?
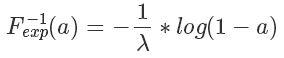
具體的映射關系可以看下圖(a),我們從 y 軸 0-1 的均勻分布樣本(綠色)映射得到了服從指數分布的樣本(紅色)。
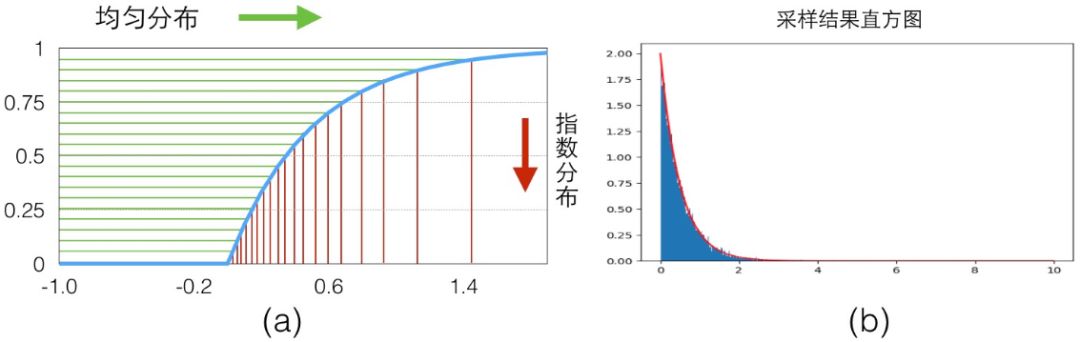
我們寫一點代碼來看看效果,最后繪制出來的直方圖可以看出來就是 exp 分布的圖,見上圖(b),可以看到隨著采樣數量的變多,概率直方圖和真實的 CDF 就越接近:
defsampleExp(Lambda=2,maxCnt=50000):ys=[]standardXaxis=[]standardExp=[]foriinrange(maxCnt):u=np.random.random()y=-1/Lambda*np.log(1-u)#F-1(X)ys.append(y)foriinrange(1000):t=Lambda*np.exp(-Lambda*i/100)standardXaxis.append(i/100)standardExp.append(t)plt.plot(standardXaxis,standardExp,'r')plt.hist(ys,1000,normed=True)plt.show()
▌Rejective Sampling
我們在學習隨機模擬的時候通常會講到用采樣的方法來計算 π 值,也就是在一個 1×1 的范圍內隨機采樣一個點,如果它到原點的距離小于 1,則說明它在1/4 圓內,則接受它,最后通過接受的占比來計算 1/4 圓形的面積,從而根據公式反算出預估的ππ值,隨著采樣點的增多,最后的結果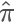 會越精準。?
會越精準。?

上面這個例子里說明一個問題,我們想求一個空間里均勻分布的集合面積,可以嘗試在更大范圍內按照均勻分布隨機采樣,如果采樣點在集合中,則接受,否則拒絕。最后的接受概率就是集合在‘更大范圍’的面積占比。
當我們重新回過頭來看想要 sample 出來的樣本服從某一個分布 p,其實就是希望樣本在其概率密度函數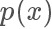 高的地方出現得更多,所以一個直覺的想法,我們從均勻分布隨機生成一個樣本?
高的地方出現得更多,所以一個直覺的想法,我們從均勻分布隨機生成一個樣本?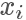 ,按照一個正比于?
,按照一個正比于?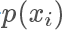 的概率接受這個樣本,也就是說雖然是從均勻分布隨機采樣,但留下的樣本更有可能是?
的概率接受這個樣本,也就是說雖然是從均勻分布隨機采樣,但留下的樣本更有可能是?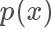 高的樣本。
高的樣本。
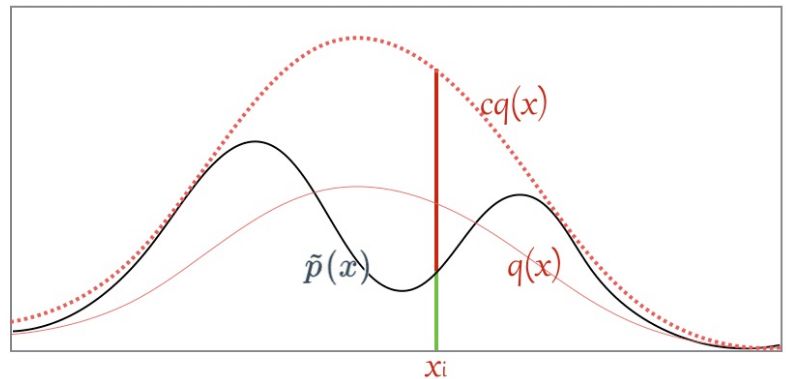
這樣的思路很自然,但是否是對的呢。其實這就是 Rejective Sampling 的基本思想,我們先看一個很 intuitive 的圖
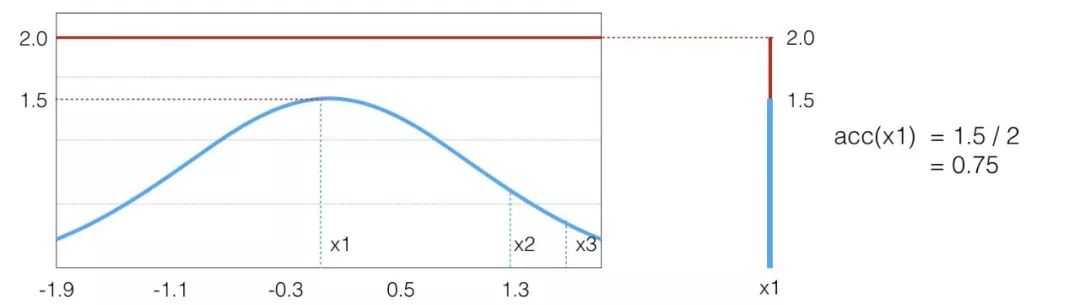
假設目標分布的 pdf 最高點是 1.5,有三個點它們的 pdf 值分別是
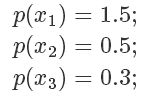
因為我們從 x 軸上是按均勻分布隨機采樣的,所以采樣到三個點的概率都一樣,也就是
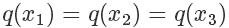
接下來需要決定每個點的接受概率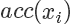 ,它應該正比于?
,它應該正比于?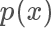 ,當然因為是概率值也需要小于等于 1.?
,當然因為是概率值也需要小于等于 1.?
我們可以畫一根 y=2 的直線,因為整個概率密度函數都在這根直線下,我們設定
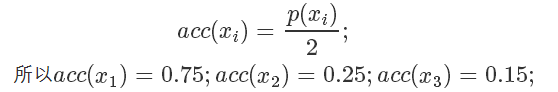
我們要做的就是生成一個 0-1的隨機數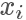 ,如果它小于接受概率?
,如果它小于接受概率?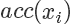 ,則留下這個樣本。因為?
,則留下這個樣本。因為?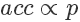 ,所以可以看到因為?
,所以可以看到因為?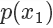 是?
是?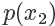 的3倍,所以?
的3倍,所以?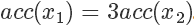 。同樣采集 100 次,最后留下來的樣本數期望也是 3 倍。這根本就是概率分布的定義!
。同樣采集 100 次,最后留下來的樣本數期望也是 3 倍。這根本就是概率分布的定義!
我們將這個過程更加形式化一點,我們我們又需要采樣的概率密度函數
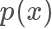 ,但實際情況我們很有可能只能計算出?
,但實際情況我們很有可能只能計算出?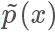 ,有
,有
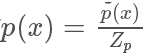
我們需要找一個可以很方便進行采樣的分布函數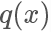 并使?
并使?
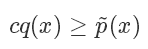
其中 c 是需要選擇的一個常數。然后我們從 q 分布中隨機采樣一個樣本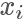 ,并以?
,并以?
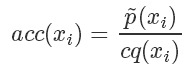
的概率決定是否接受這個樣本。重復這個過程就是「拒絕采樣」算法了。
在上面的例子我們選擇的 q 分布是均勻分布,所以從圖像上看其 pdf 是直線,但實際上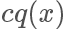 和?
和?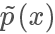 越接近,采樣效率越高,因為其接受概率也越高:?
越接近,采樣效率越高,因為其接受概率也越高:?
▌Importance Sampling
上面描述了兩種從另一個分布獲取指定分布的采樣樣本的算法,對于1.在實際工作中,一般來說我們需要 sample 的分布都及其復雜,不太可能求解出它的反函數,但 p(x) 的值也許還是可以計算的。對于2.找到一個合適的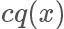
那我們回過頭來看我們sample的目的:其實是想求得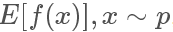 ,也就是?
,也就是?
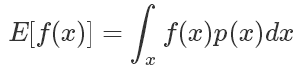
如果符合 p(x) 分布的樣本不太好生成,我們可以引入另一個分布 q(x),可以很方便地生成樣本。使得
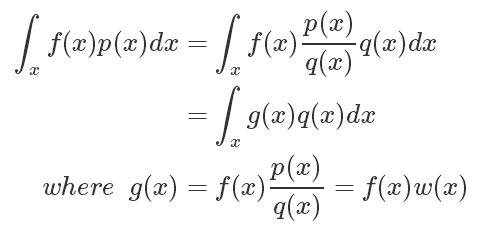
我們將問題轉化為了求 g(x) 在 q(x) 分布下的期望!!!
我們稱其中的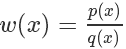 叫做?Importance Weight.
叫做?Importance Weight.
▌Importance Sample 解決的問題
首先當然是我們本來沒辦法 sample from p,這個是我們看到的,IS 將之轉化為了從 q 分布進行采樣;同時 IS 有時候還可以改進原來的 sample,比如說:
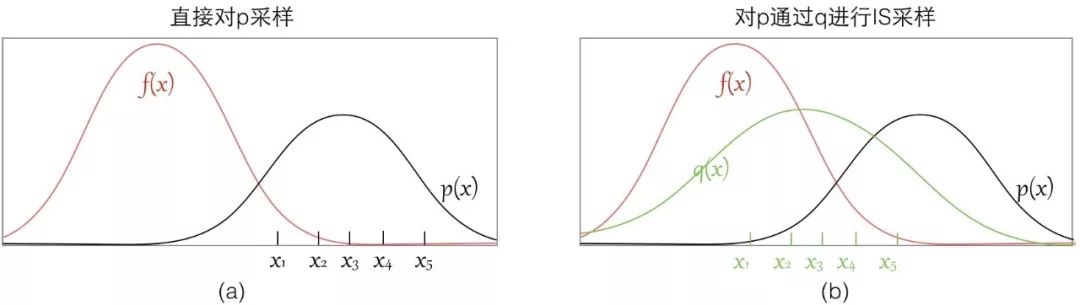
可以看到如果我們直接從 p 進行采樣,而實際上這些樣本對應的 f(x) 都很小,采樣數量有限的情況下很有可能都無法獲得 f(x) 值較大的樣本,這樣評估出來的期望偏差會較大;
而如果我們找到一個 q 分布,使得它能在 f(x)*p(x) 較大的地方采集到樣本,則能更好地逼近 [Ef(x)],因為有 Importance Weight 控制其比重,所以也不會導致結果出現過大偏差。
所以選擇一個好的p也能幫助你sample出來的效率更高,要使得 f(x)p(x)較大的地方能被 sample出來。
▌無法直接求得p(x)的情況
上面我們假設 g(x) 和 q(x) 都可以比較方便地計算,但有些時候我們這個其實是很困難的,更常見的情況市我們能夠比較方便地計算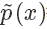 和?
和?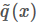
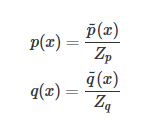
其中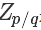 是一個標準化項(常數),使得?
是一個標準化項(常數),使得?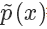 或者?
或者?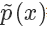 等比例變化為一個概率分布,你可以理解為 softmax 里面那個除數。也就是說?
等比例變化為一個概率分布,你可以理解為 softmax 里面那個除數。也就是說?
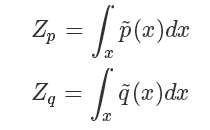
這種情況下我們的 importance sampling 是否還能應用呢?
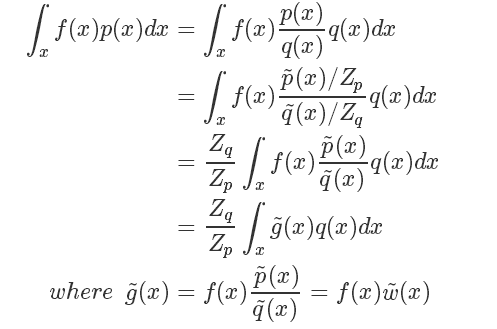
而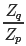 我們直接計算并不太好計算,而它的倒數:?
我們直接計算并不太好計算,而它的倒數:?
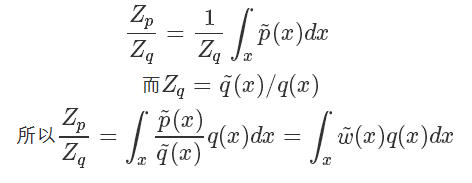
因為我們家設能很方便地從 q 采樣,所以上式其實又被轉化成了一個蒙特卡洛可解的問題,也就是
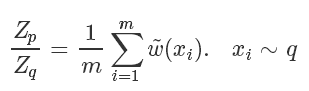
最終最終,原來的蒙特卡洛問題變成了:
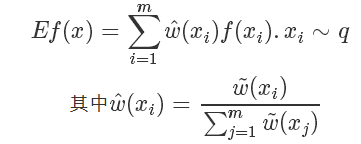
所以我們完全不用知道 q(x) 確切的計算值,就可以近似地從中得到在 q 分布下 f(x) 的取值!!amazing!
▌Importance Sampling在深度學習里面的應用
在深度學習特別是NLP的Language Model中,訓練的時候最后一層往往會使用 softmax 函數并計算相應的梯度。
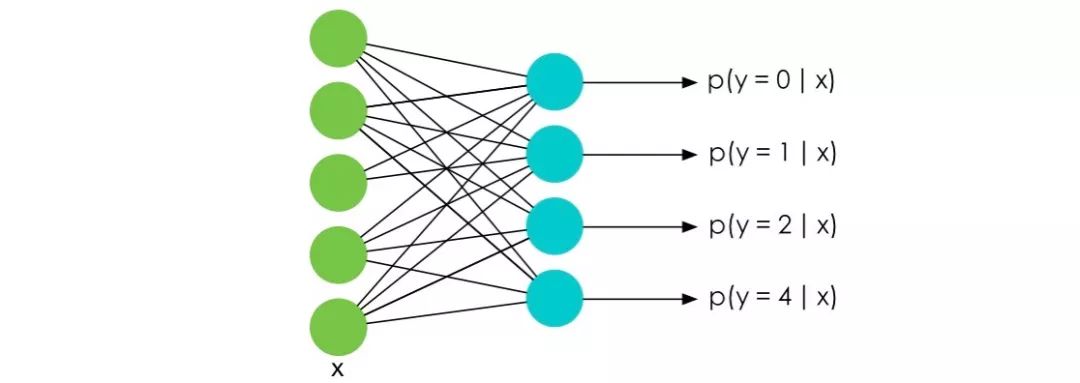
而我們知道 softmax 函數的表達式是:
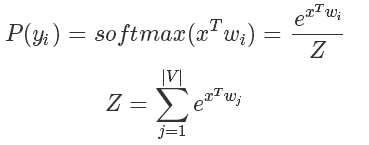
要知道在 LM 中 m 的大小是詞匯的數量決定的,在一些巨大的模型里可能有幾十萬個詞,也就意味著計算Z的代價十分巨大。
而我們在訓練的時候無非是想對 softmax 的結果進行求導,也就是說
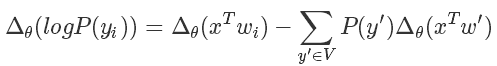
后面那一塊,我們好像看到了熟悉的東西,沒錯這個形式就是為采樣量身定做似的。
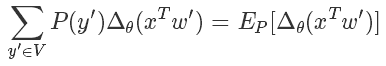
經典的蒙特卡洛方法就可以派上用途了,與其枚舉所有的詞,我們只需要從 V 里 sample 出一些樣本詞,就可以近似地逼近結果了。
同時直接從 P 中 sample 也不可取的,而且計算 P是非常耗時的事情(因為需要計算Z),我們一般只能計算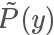 ,而且直接從 P 中 sample 也不可取,所以我們選擇另一個分布 Q 進行 Importance Sample 即可。
,而且直接從 P 中 sample 也不可取,所以我們選擇另一個分布 Q 進行 Importance Sample 即可。
一般來說可能選擇的 Q 分布是簡單一些的 n-gramn 模型。下面是論文中的算法偽代碼,基本上是比較標準的流程(論文圖片的符號和上面的描述稍有出入,理解一下過程即可):

References
【1】mathematicalmonk’s machine learning course on y2b. machine learing
【2】Pattern Recognition And Machine Learning
【3】Adaptive Importance Sampling to Accelerate Trainingof a Neural Probabilistic Language Model.Yoshua Bengio and Jean-Sébastien Senécal.
?
采樣方法 2
▌引子
在上面我們講到了拒絕采樣、重要性采樣一系列的蒙特卡洛采樣方法,但這些方法在高維空間時都會遇到一些問題,因為很難找到非常合適的可采樣Q分布,同時保證采樣效率以及精準度。
本文將會介紹采樣方法中最重要的一族算法,MCMC(Markov Chain Monte Carlo),在之前我們的蒙特卡洛模擬都是按照如下公式進行的:
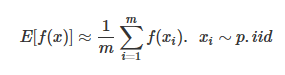
我們的x都是獨立采樣出來的,而在MCMC中,它變成了
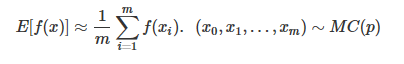
其中的MC(p)就是我們本文的主角之一,馬爾可夫過程(Markov Process)生成的馬爾可夫鏈(Markov Chain)。
▌Markov Chain(馬爾可夫鏈)
在序列的算法(一·a)馬爾可夫模型中(https://blog.csdn.net/dark_scope/article/details/61417336)我們就說到了馬爾可夫模型的馬爾可夫鏈,簡單來說就是滿足馬爾可夫假設
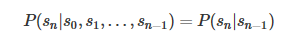
的狀態序列,由馬爾可夫過程(Markov Process)生成。
一個馬爾可夫過程由兩部分組成,一是狀態集合Ω,二是轉移概率矩陣T。
其流程是:選擇一個初始的狀態分布π0,然后進行狀態的轉移:
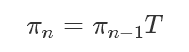
得到的π0,π1,π2 ...πn 狀態分布序列。
注意:我們在這里講的理論和推導都是基于離散變量的,但其實是可以直接推廣到連續變量。
馬爾可夫鏈在很多場景都有應用,比如大名鼎鼎的 pagerank 算法,都用到了類似的轉移過程;
馬爾可夫鏈在某種特定情況下,有一個奇妙的性質:在某種條件下,當你從一個分布π0開始進行概率轉移,無論你一開始π0 的選擇是什么,最終會收斂到一個固定的分布π,叫做穩態(steady-state)。
穩態滿足條件:
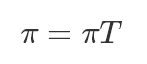
這里可以參考《LDA數學八卦0.4.2》的例子,非常生動地描述了社會階層轉化的一個例子,也對MCMC作了非常好的講解
書歸正傳,回到我們采樣的場景,我們知道,采樣的難點就在于概率密度函數過于復雜而無法進行有效采樣,如果我們可以設計一個馬爾可夫過程,使得它最終收斂的分布是我們想要采樣的概率分布,不就可以解決我們的問題了么。
前面提到了在某種特定情況下,這就是所有MCMC算法的理論基礎ErgodicTheorem:
如果一個離散馬爾可夫鏈(x0,x1...xm)是一個與時間無關的 Irreducible 的離散,并且有一個穩態分布π,則:

它需要滿足的條件有這樣幾個,我們直接列在這里,不作證明:????????????????
1.Time homogeneous: 狀態轉移與時間無關,這個很好理解。2.Stationary Distribution: 最終是會收斂到穩定狀態的。3.Irreducible: 任意兩個狀態之間都是可以互相到達的。4.Aperiodic:馬爾可夫序列是非周期的,我們所見的絕大多數序列都是非周期的。
雖然這里要求是離散的馬爾可夫鏈,但實際上對于連續的場景也是適用的,只是轉移概率矩陣變成了轉移概率函數。
▌MCMC
在上面馬爾可夫鏈中我們的所說的狀態都是某個可選的變量值,比如社會等級上、中、下,而在采樣的場景中,特別是多元概率分布,并不是量從某個維度轉移到另一個維度,比如一個二元分布,二維平面上的每一個點都是一個狀態,所有狀態的概率和為 1! 這里比較容易產生混淆,一定小心。
在這里我們再介紹一個概念:
Detail balance:一個馬爾可夫過程是細致平穩的,即對任意 a,b 兩個狀態:
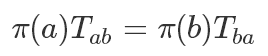
細致平穩條件也可以推導出一個非周期的馬爾可夫鏈是平穩的,因為每次轉移狀態i從狀態j獲得的量與 j 從 i 獲得的量是一樣的,那毫無疑問最后πT=π.
所以我們的目標就是需要構造這樣一個馬爾可夫鏈,使得它最后能夠收斂到我們期望的分布π,而我們的狀態集合其實是固定的,所以最終目標就是構造一個合適的 T,就大功告成了。
一般來說我們有:
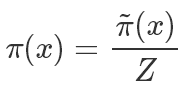
其中Z是歸一化參數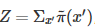 ,因為我們通常能夠很方便地計算分子
,因為我們通常能夠很方便地計算分子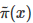 ,但是分母的計算因為要枚舉所有的狀態所以過于復雜而無法計算。我們希望最終采樣出來的樣本符合?π 分布。
,但是分母的計算因為要枚舉所有的狀態所以過于復雜而無法計算。我們希望最終采樣出來的樣本符合?π 分布。
▌Metropolis
原理描述
Metropolis 算法算是 MCMC 的開山鼻祖了,它這里假設我們已經有了一個狀態轉移概率函數T來表示轉移概率,T(a,b) 表示從 a 轉移到 b 的概率(這里T的選擇我們稍后再說),顯然通常情況下一個T是不滿足細致平穩條件的:
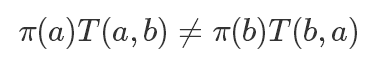
所以我們需要進行一些改造,加入一項Q使得等式成立:
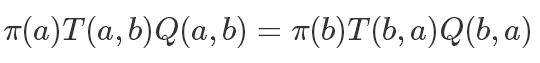
基于對稱的原則,我們直接讓
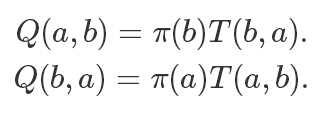
所以我們改造后的滿足細致平穩條件的轉移矩陣就是:
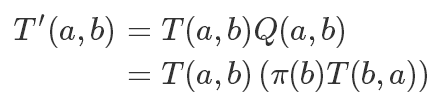
在 Metropolis 算法中,這個加入的這個 Q 項是此次轉移的接受概率,是不是和拒絕采樣有點神似。

但這里還有一個問題,我們的接受概率 Q 可能會非常小,而且其中還需要精確計算出π(x′),這個我們之前提到了是非常困難的,再回到我們的細致平穩條件:
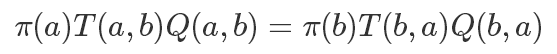
如果兩邊同時乘以一個數值,它也是成立的,比如
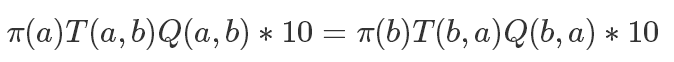
所以我們可以同步放大Q(a,b)和Q(b,a),使得其中最大的一個值為1,也就是說:
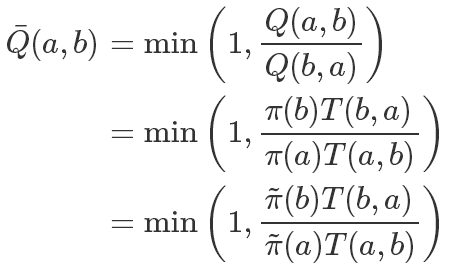
這樣在提高接受率的同時,因為除式的存在我們還可以約掉難以計算的 Z。

代碼實驗
我們之前提到狀態轉移函數T的選擇,可以看到如果我們選擇一個對稱的轉移函數,即T(a,b)=T(b,a),上面的接受概率還可以簡化為
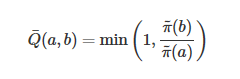
這也是一般 Metropolis 算法中采用的方法,T使用一個均勻分布即可,所有狀態之間的轉移概率都相同。
實驗中我們使用一個二元高斯分布來進行采樣模擬
其概率密度函數這樣計算的,x是一個二維坐標:
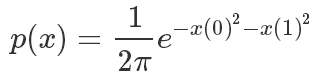
defget_p(x):#模擬pi函數return1/(2*PI)*np.exp(-x[0]**2-x[1]**2)defget_tilde_p(x):#模擬不知道怎么計算Z的PI,20這個值對于外部采樣算法來說是未知的,對外只暴露這個函數結果returnget_p(x)*20
每輪采樣的函數:
defdomain_random():#計算定義域一個隨機值returnnp.random.random()*3.8-1.9defmetropolis(x):new_x=(domain_random(),domain_random())#新狀態#計算接收概率acc=min(1,get_tilde_p((new_x[0],new_x[1]))/get_tilde_p((x[0],x[1])))#使用一個隨機數判斷是否接受u=np.random.random()ifu
然后就可以完整地跑一個實驗了:
deftestMetropolis(counts=100,drawPath=False):plotContour()#可視化#主要邏輯x=(domain_random(),domain_random())#x0xs=[x]#采樣狀態序列foriinrange(counts):xs.append(x)x=metropolis(x)#采樣并判斷是否接受#在各個狀態之間繪制跳轉的線條幫助可視化ifdrawPath:plt.plot(map(lambdax:x[0],xs),map(lambdax:x[1],xs),'k-',linewidth=0.5)##繪制采樣的點plt.scatter(map(lambdax:x[0],xs),map(lambdax:x[1],xs),c='g',marker='.')plt.show()pass
可以看到采樣結果并沒有想象的那么密集,因為雖然我們提高了接受率,但還是會拒絕掉很多點,所以即使采樣了5000次,繪制的點也沒有密布整個畫面。
▌Gibbs Sampling
算法分析
通過分析 Metropolis 的采樣軌跡,我們發現前后兩個狀態之間并沒有特別的聯系,新的狀態都是從 T 采樣出來的,而因為原始的分布很難計算,所以我們選擇的T是均勻分布,因此必須以一個概率進行拒絕,才能保證最后收斂到我們期望的分布。
如果我們限定新的狀態只改變原狀態的其中一個維度,即
只改變了其中第 j 個維度,則有
其中
結論很清晰:這樣一個轉移概率函數T是滿足細致平穩條件的,而且和Metropolis里面不同:它不是對稱的。
我們能夠以 1 為概率接受它的轉移結果。
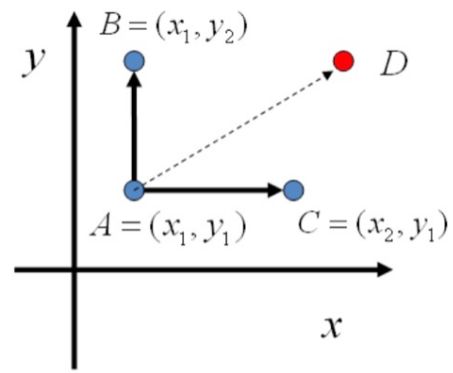
以一個二元分布為例,在平面上:
A 只能跳轉到位于統一條坐標線上的 B,C 兩個點,對于 D,它無法一次轉移到達,但是可以通過兩次變換到達,仍然滿足Irreducible的條件。
這樣構造出我們需要的轉移概率函數T之后,就直接得到我們的 Gibbs 采樣算法了:
代碼實驗
想必大家發現了,如果要寫代碼,我們必須要知道如何從
在我們之前實驗的場景(二元正態分布),確實也能精確地寫出這個概率分布的概率密度函數(也是一個正態分布)。
但退一步想,現在我們只關心一元的采樣了,所以其實是有很多方法可以用到的,比如拒絕采樣等等。
而最簡單的,直接在這一維度上隨機采幾個點,然后按照它們的概率密度函數值為權重選擇其中一個點作為采樣結果即可。
代碼里這樣做的目的主要是為了讓代碼足夠簡單,只依賴一個均勻分布的隨機數生成器。
defpartialSampler(x,dim):xes=[]fortinrange(10):#隨機選擇10個點xes.append(domain_random())tilde_ps=[]fortinrange(10):#計算這10個點的未歸一化的概率密度值tmpx=x[:]tmpx[dim]=xes[t]tilde_ps.append(get_tilde_p(tmpx))#在這10個點上進行歸一化操作,然后按照概率進行選擇。norm_tilde_ps=np.asarray(tilde_ps)/sum(tilde_ps)u=np.random.random()sums=0.0fortinrange(10):sums+=norm_tilde_ps[t]ifsums>=u:returnxes[t]
主程序的結構基本上和之前是一樣的,
defgibbs(x):rst=np.asarray(x)[:]path=[(x[0],x[1])]fordiminrange(2):#維度輪詢,這里加入隨機也是可以的。new_value=partialSampler(rst,dim)rst[dim]=new_valuepath.append([rst[0],rst[1]])#這里最終只畫出一輪輪詢之后的點,但會把路徑都畫出來returnrst,pathdeftestGibbs(counts=100,drawPath=False):plotContour()x=(domain_random(),domain_random())xs=[x]paths=[x]foriinrange(counts):xs.append([x[0],x[1]])x,path=gibbs(x)paths.extend(path)#存儲路徑ifdrawPath:plt.plot(map(lambdax:x[0],paths),map(lambdax:x[1],paths),'k-',linewidth=0.5)plt.scatter(map(lambdax:x[0],xs),map(lambdax:x[1],xs),c='g',marker='.')plt.show()
采樣的結果:
??????????????
其轉移的路徑看到都是與坐標軸平行的直線,并且可以看到采樣 5000 詞的時候跟 Metropolis 相比密集了很多,因為它沒有拒絕掉的點。
▌后注
本文我們講述了MCMC里面兩個最常見的算法Metropolis和Gibbs Sampling,以及它們各自的實現
從采樣路徑來看:
Metropolis 是完全隨機的,以一個概率進行拒絕;
而 Gibbs Sampling 則是在某個維度上進行轉移。
如果我們仍然希望最后使用獨立同分布的數據進行蒙特卡洛模擬,只需要進行多次 MCMC,然后拿每個 MCMC 的第 n 個狀態作為一個樣本使用即可。
完整的代碼見鏈接:
https://github.com/justdark/dml/blob/master/dml/tool/mcmc.py
因為從頭到尾影響分布的只有get_p()函數,所以如果我們想對其他分布進行實驗,只需要改變這個函數的定義就好了,比如說我們對一個相關系數為0.5 的二元正態分布,只需要修改 get_p() 函數:
defget_p(x):return1/(2*PI*math.sqrt(1-0.25))*np.exp(-1/(2*(1-0.25))*(x[0]**2-x[0]*x[1]+x[1]**2))
就可以得到相應的采樣結果:
而且因為這里并不要求p是一個歸一化后的分布,可以嘗試任何>0的函數,比如
defget_p(x):returnnp.sin(x[0]**2+x[1]**2)+1
也可以得到采樣結果:
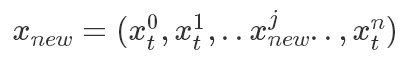
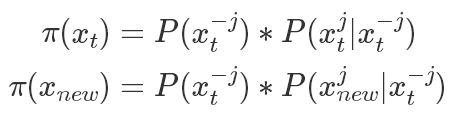
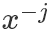 表示除了第j元其他的變量。?所以有(以
表示除了第j元其他的變量。?所以有(以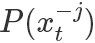 為橋梁作轉換很好得到):?
為橋梁作轉換很好得到):?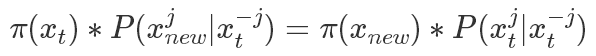


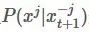 進行采樣,這是一個后驗的概率分布,在很多應用中是能夠定義出函數表達的。
進行采樣,這是一個后驗的概率分布,在很多應用中是能夠定義出函數表達的。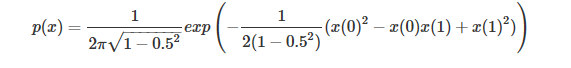
-
函數
+關注
關注
3文章
4333瀏覽量
62686 -
采樣
+關注
關注
1文章
121瀏覽量
25572 -
機器學習
+關注
關注
66文章
8422瀏覽量
132714
原文標題:一文了解采樣方法
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
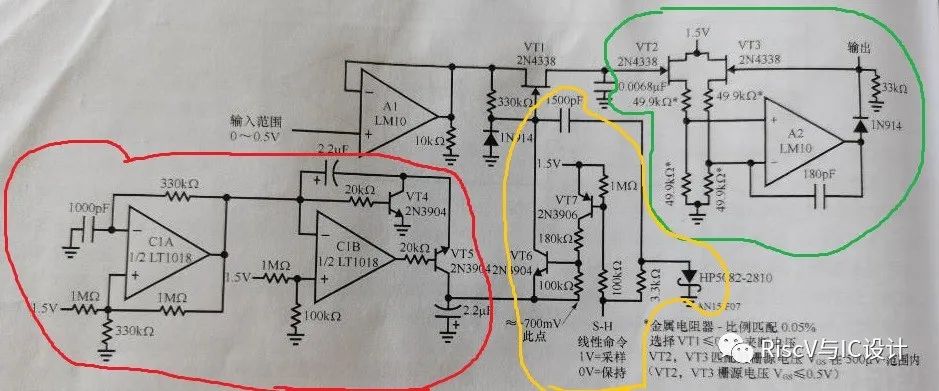
傳統的模擬電壓采樣保持電路方案

STM32F中AD采樣的方法有哪些
用于圖像分類的有偏特征采樣方法
空間曲線基于內在幾何量的均勻采樣方法

隨機采樣方法拒絕采樣思想





 經典的采樣方法有哪些?
經典的采樣方法有哪些?











評論