電動機械是現代工業社會的重要支柱。在這類種類繁多的機械設備中,發電機或電動機一類的旋轉機械應用最為廣泛。COMSOL Multiphysics 中的旋轉機械,磁物理場接口即旨在模擬這些系統。請跟隨我們一起探討旋轉機械的模擬過程,并了解使用此功能詳細的最佳做法。
旋轉機械的幾何
任何一種旋轉磁力機械都包含兩個零件:定子和轉子,中間有空氣縫隙將其分隔開,并驅使轉子旋轉。因為有限元方法不支持旋轉,所以旋轉機械,磁接口利用移動網格的方法模擬這種旋轉。
直流換向電機的幾何,其中包含兩個永磁體和一個旋轉繞組。
這種機械的幾何切割(通常沿著空氣縫隙)成兩部分:一部分包含定子,另一部分包含轉子。之后這兩部分分別進行網格剖分。在模擬過程中,含有定子的部分保持靜止,含有轉子的部分則旋轉。這兩部分以及相應的網格一直在切割邊界相接觸。
幾何必須包含兩磁體間的空氣縫隙。紅色表示一條可能的切割邊界。
默認情況下,幾何序列的最后一步是形成聯合體、合并所有幾何對象并作為一個對象進行網格剖分,最終完成定型。在分別對這兩部分進行網格剖分之前,必須通過形成裝配使對象定型。首先利用并集與其他操作,為靜止部分和旋轉部分分別創建一個幾何對象。隨后對幾何序列的定型節點選擇形成裝配。定型過程中,一致對會自動創建在定義下,表示這兩個對象的共同(接觸)邊界。
直流電機的網格放大圖。旋轉部分和靜止部分已分別進行了網格剖分,在圖中顯示為兩側不同的網格節點位置。邊界高亮顯示為藍色,包含在一致對中。在旋轉過程中,這兩部分的網格彼此滑動,在一致對上保持接觸。
現在就可以使用旋轉機械,磁接口定義系統的動力學了。使用指定旋轉特征指定旋轉角(可指定為與時間相關),或使用指定旋轉速度特征輸入一個恒定的角速度。應用以上任一個特征后,COMSOL Multiphysics 軟件將對選定域啟用移動網格功能,同時設置合適的電磁場變換。
“指定旋轉”特征或“指定旋轉速度”特征必須應用到包含轉子的旋轉部分。
切割處會怎樣變化呢?從物理角度而言,空氣縫隙處的電磁場是連續的,并假定材料均勻。與其他內部邊界不同的是,一致對處的磁場不會自動連續。要強制其連續,須對一致對使用連續性對特征。
混合公式
旋轉機械,磁接口通過求解 Maxwell 方程計算電磁場的分布。在各個物理場確定后,就能計算出大部分相關的物理量(如施加的扭矩)。在瞬態分析中,這個接口應用了準靜態近似,這一方法會忽略位移電流密度,或者近似認為機械的電容效應可忽略。完成近似處理后,機械中的全部電流要么是外加的(也就是通過勵磁繞組),要么是機械的導電部件感應產生的渦流。不導電部分(如空氣間隙)不會產生任何電流密度。
該接口使用兩種方法求解 Maxwell 方程:矢量勢公式和標量勢公式。第一種方法引入矢量場 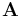
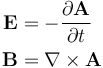
有了 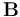
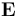
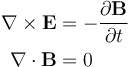
要求解的安培定律為:
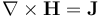
矢量勢公式用于磁場物理場接口。
標量勢公式僅適用于電流密度為零的區域。針對本文討論的旋轉機械,我們引入了標量場 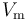
與矢量勢公式相比,標量勢公式引入的自由度較少,因此求解的問題“更簡單”。當然,其缺點也很明顯,只能用在無電流區域。通常,因為這個缺陷,標量勢公式只適用于非常特殊的情況,如永磁體的穩態研究等。不過,由于應用了準靜態近似,標量勢公式還能用于瞬態分析中的非傳導區域。
在三維模型的情況中,標量勢方法具有另一個重要的優點。當與連續性特征這樣的成對特征配合使用時,這個公式能確保磁通密度的耦合更加精確,而磁通密度正是磁力機械模擬的核心。
這兩個公式可以一起使用,即將矢量勢公式用于傳導域或導電域,標量勢公式用于空氣縫隙和非傳導域。因此稱為混合公式,在三維模型中,由于標量公式提高了成對耦合的精度,所以這種方法特別有用。在二維模型中,對于平面內的磁場,用于矢量勢和標量勢的離散化方式很相似。所以在二維平面內的情況中不必使用混合公式。
旋轉機械,磁接口默認將安培定律特征(即矢量勢公式)應用到所有域,因為這是最通用的公式。將磁通量守恒特征(實現標量勢公式)應用到空氣縫隙和其他非傳導性區域等無電流的域內,以替代安培定律。使用混合公式邊界特征后會在標量勢區域和矢量勢區域間的界面上應用適當的條件。請注意,連續性對特征會耦合一致對兩側的相關變量,所以要確保兩側使用了相同的公式。為提高數值穩定性,將磁標勢場度規修復特征應用于全部矢量勢域,這是磁場接口中常見的做法。
“安培定律”特征僅應用于包含導電繞組的旋轉部分的內部。注意,選定區域小于整個旋轉部分,旋轉部分延伸到切割邊界。要提高精度,在一致對條件附近使用標量勢公式。
混合公式非常簡單明了,但請牢記它的數學背景和局限性。判斷是否適用的最重要條件,也是最易出錯的條件,即標量勢只能表示不旋轉的磁場(無旋磁場)。在實際情況中,標量勢區域不可能存在完全圍住(“鎖住”)電流的閉合曲線。
其原因來自標量勢的定義和 Maxwell 方程。在使用標量勢公式的區域,沿閉合曲線的磁場積分始終為零,因為磁場是標量勢的梯度。與此同時,通過安培定律,我們知道沿閉合曲線的磁場積分必須等于該曲線圍住的總電流。因此,除非圍住的電流恰好為零,否則不會有解(也不可能有標量勢的配置)。如果我們試圖用 COMSOL Multiphysics 求解一個不滿足此條件的問題,那么求解器不會收斂。下圖闡明了這個概念,其中藍色表示矢量勢區域,灰色圍住的是標量勢區域。
標量勢區域中一條閉合曲線“鎖住”導電(電流返回路徑在幾何之外)的標量勢區域。此模型可能無解。
下圖為有效幾何,其中標量勢區域簡單相連,意味著全程沒有矢量勢“漏洞”。
相對運動和框架
對于旋轉機械而言,定子和轉子的相對運動是機械運行的核心。相對運動物體的電磁問題并非不值一提,事實上,一百多年以前,正是這個問題推動了相對論的發展。
通常而言,解決這類問題的第一步是選擇表述方程時所用的框架。框架即選擇坐標系以及選擇空間每一點的軸。一個很自然的選擇是固定的笛卡爾坐標系,有時稱為“實驗室”框架,在 COMSOL Multiphysic 中稱為空間框架。在這個框架中,靜止部分固定不動,旋轉部分運動。
另一個可能的選擇是,將笛卡爾坐標系應用到空間的每一點,如同空間框架中的那樣,不過隨后要使坐標系跟隨旋轉點運動。在這個框架中,構成機械的材料始終靜止(框架本身隨之運動),所以稱為材料框架。在機械的靜止部分,空間框架和材料框架重合,因為這部分沒有任何運動。而在旋轉部分,材料框架相對于空間框架發生旋轉。只要應用適當的變換,這兩種框架產生的結果完全相同。
默認情況下,材料框架的坐標系為大寫字母 (X, Y, Z),空間框架的坐標系為小寫字母 (x,y, z)。坐標系的名稱表示特定框架內矢量的分量;例如,電場分量在空間框架中表示為 Ex、Ey 和 Ez,在材料框架中表示為 EX、EY 和 EZ。
這一問題會自動用公式表示,并通過材料框架中的物理場求解。至于后處理,觀察空間框架中的變量和各個物理場通常很有趣,因為定子始終靜止,它與這幾個物理量形成了鮮明的對比。因此,物理場會自動變換,并在空間框架中定義所有矢量場。空間變量和材料變量在表達式列表中表示為帶括號的框架,如下圖所示。

矢量物理量定義為空間框架和材料框架中的分量。
從材料框架變換到空間框架時,大多數矢量物理量僅進行旋轉,而模保持不變。但電磁場,尤其是電場卻并非如此,因為它們遵循洛倫茲變換規則進行變換。對于非相對論速度,用以下公式將這兩個框架內的物理場關聯起來:
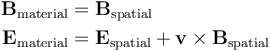
我們先觀察二維發電機的幾何。下圖中,紅線將旋轉部分和靜止部分分隔開。深色域表示轉子中的永磁體,淺色域表示可飽和鐵,銅域表示發電機的繞組。白色域表示空氣。
傳導性材料“觀察到”材料框架中的電場,驅動電流密度。總之,這個電場與空間框架中的電場完全不同,如下圖所示。
左圖:旋轉時空間框架中電場的平面外分量(單位: V/m)。轉子中的磁體相對于實驗室框架內的定子發生運動,因此產生感應電場。右圖:材料框架中電場的平面外分量(單位 :V/m)。因為旋轉部分的框架中磁體靜止,所以不會產生明顯的感應電場。靜止部分的電場在材料框架和空間框架中完全相同。
設置求解器
求解器必須按照預期的仿真進行專門設置。穩態研究可用于模擬穩態條件下(即轉子固定且瞬態效應消失后)旋轉機械的行為。瞬態步驟則研究旋轉時發生的情況。
使用瞬態步驟時,很重要的一點是指定正確的初始值,該值須經調查符合實際情況。如果這是研究的第一步,那么可以從初始值特征(默認設置為零)獲取磁場的初始值。另一種方法是,在瞬態研究步驟之前求解“穩態”步驟,以使瞬態仿真的初始值不為零。
總之,如果激勵“已激活”(例如發電機中的永磁體),則添加穩態步驟,這與激勵在瞬態研究開始時才“打開”完全不同。在例如直流換向電機這樣具有兩種激勵形式的模型中,一定要禁用會導致“穩態”步驟中產生瞬態激勵的特征,也就是說,如果仿真的目的是模擬瞬態激勵“打開”時的行為,則禁用這樣的特征。
總結
模擬旋轉機械在本質上是一個高級的、具有挑戰性的主題。在本文中,我們展示了旋轉磁力機械模擬時涉及的一些概念,以及處理此類有趣應用的步驟和最佳做法。旋轉機械,磁接口和磁場接口構成了這一功能的核心,是分析和優化復雜系統的強大工具。
-
直流電機
+關注
關注
36文章
1710瀏覽量
70237 -
網格
+關注
關注
0文章
139瀏覽量
16026 -
旋轉機械
+關注
關注
1文章
27瀏覽量
11337
原文標題:使用 COMSOL Multiphysics 模擬三維旋轉機械
文章出處:【微信號:COMSOL-China,微信公眾號:COMSOL】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
邏輯電平的一些基本概念詳細說明

TensorFlow主題演講中涉及的一些更新總結
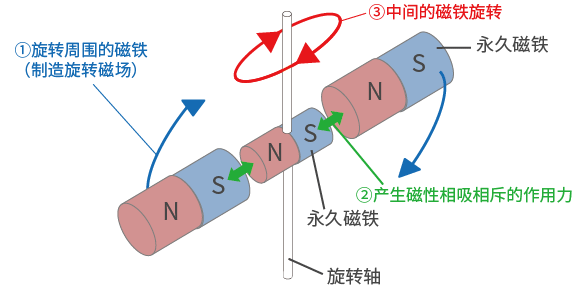
電機旋轉借助磁鐵、磁力




 旋轉磁力機械模擬時涉及的一些概念
旋轉磁力機械模擬時涉及的一些概念










評論