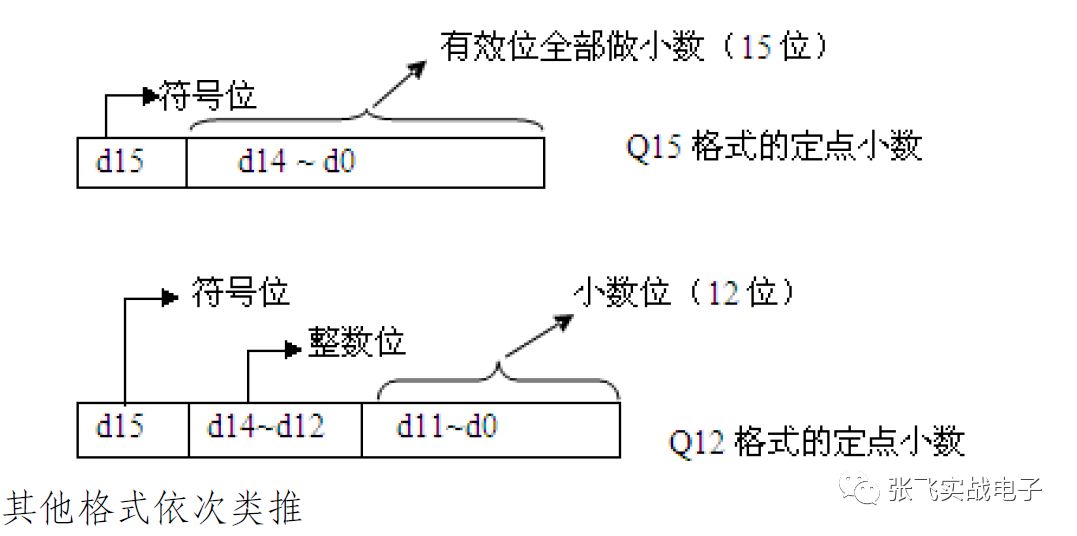
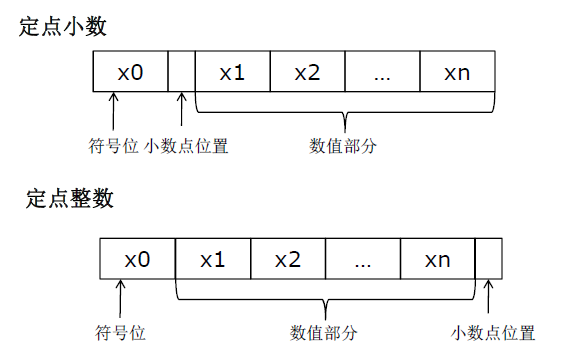
許多MCU 芯片只支持整數運算，如果要在這些芯片上進行小數運算，定點運算應該是最佳選擇了；此外即使芯片支持浮點數，定點小數運算也是最佳的速度選擇。所謂定點小數運算，就是將小數點位置固定，用整數的方式來進行運算；由于小數點的位置是固定的，所以就沒有必要儲存它。既然沒有儲存小數點的位置，那么計算機當然就不知道小數點的位置，所以這個小數點的位置是我們寫程序的人自己需要牢記的。那么，如何將小數表示成整數呢？

處理器整數以二進制形式存儲，首先要了解如何將小數轉換成二進制！假定MCU 是16位，因最高位是符號位，那么有效位就只有15位(不考慮符號則16位)。即小數點之后可以有0~15 位。我們把小數點之后有n位叫做Qn，例如小數點之后有12位叫做Q12 格式的定點小數，而Q0就是我們所說的整數:

以Q12 格式為例，Q12 的正數的最大值是0111.111111111111，第一個0是符號位，后面的數都是1，那么這個數是十進制的多少呢？ 請看下面的運算：

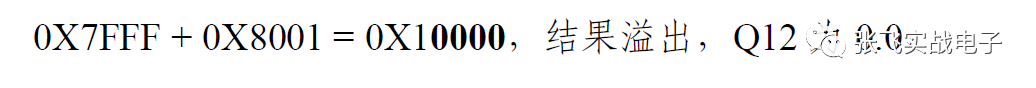
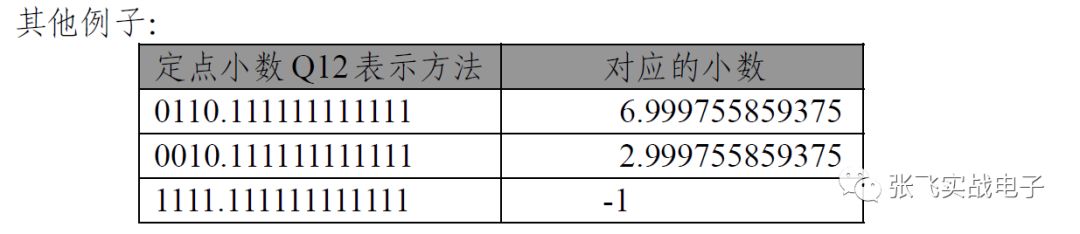
對于Qn格式的定點小數的表達的數值就它的整數值除以2^Qn。在計算機中還是以整數來運算，我們把它想象成實際所表達的值的時候，進行這個運算。反過來把一個實際所要表達的值x 轉換Qn 型的定點小數的時候，就是x*(2^ Qn)了。例如0.2 的Q12 型定點小數為：0.2*(2^12) =819.2，由于這個數要用整數儲存， 所以是819 即0x0333。因為舍棄了小數部分，所以0x0333 不是精確的0.2，實際上它是819/2^12=0.199951171875，非常接近0.2 了。

因此我們可以歸納出一個公式，假定x 表示實際的小數， q表示這小數在MCU 中的Qn 型定點小數，則有：

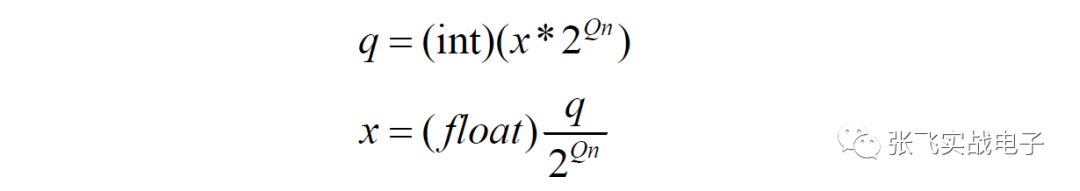
由以上公式我們可以很快得出定點小數運算法則：

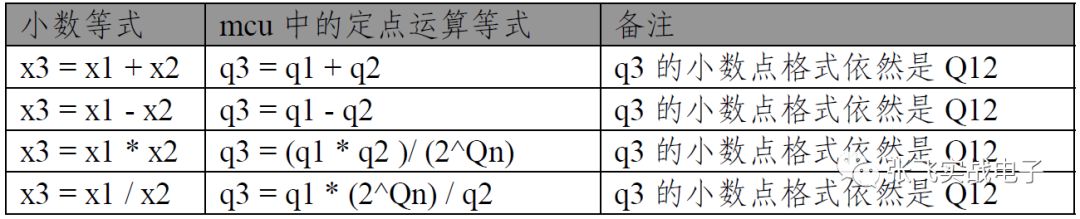
加減法和一般的整數運算相同，而乘除法的時候，為了使得結果的小數點位不移動，對數值進行了移動（乘除2^Qn實際是將被乘除數左或右移動n位）：

q3 = q1 * q2 / (2^Qn) ---> q3 = (q1 * q2 )>>Qn

用c語言來寫定點小數的乘法就是：

short q1,q2,q3;

....

q3=((long q1) * (long q2)) >> n;

由于/ 2^Qn 和* 2^Qn可以簡單的用移位來計算，所以定點小數的運算比浮點小數要快得多。下面我們用一個例子來驗證一下上面的公式：用Q12來計算2.1 * 2.2，先把2.1, 2.2轉換為Q12 定點小數：

2.1 * 2^12 = 8601.6 = 8602

2.2 * 2^12 = 9011.2 = 9011

(8602 * 9011) >> 12 = 18923

18923 的實際值是18923/(2^12) = 4.619873046875 和實際的結果4.62相差0.000126953125，對于一般的計算已經足夠精確了。好了，話不投機半句多，說了這么多，最終還是要用實例代碼來形象的指出如何實現定點運算。

MCU 實例

用碩呈16BIT-MCU 實現一組數據乘以0.492，這組數據是：

100*0.492=49.2

105*0.492=51.66

147*0.492=72.324

350*0.492=172.2

860*0.492=423.12

458*0.492=225.336

步驟一，先確定小數，0.492屬于小于“1”的小數；且乘數與被乘數符號都為正，為了提高精度，可以考慮使用Q16 格式；因此將0.492轉換成定點小數有：

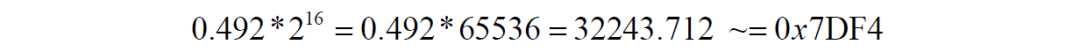
步驟二，編寫如下代碼：

在地址0x00F0 處，設定運算為無符號乘以無符號運算。

地址0x00F1 處，將Q16 小數送入MX 寄存器。

地址0x00f4~0x00f8 處，利用循環計算出_MUL_表格中列出的數據，并將結果存到I0指向的緩沖中（MR1 是計算結果的整數位，MR0 是計算結果的小數低位）。

計算結果請查閱以下表格：

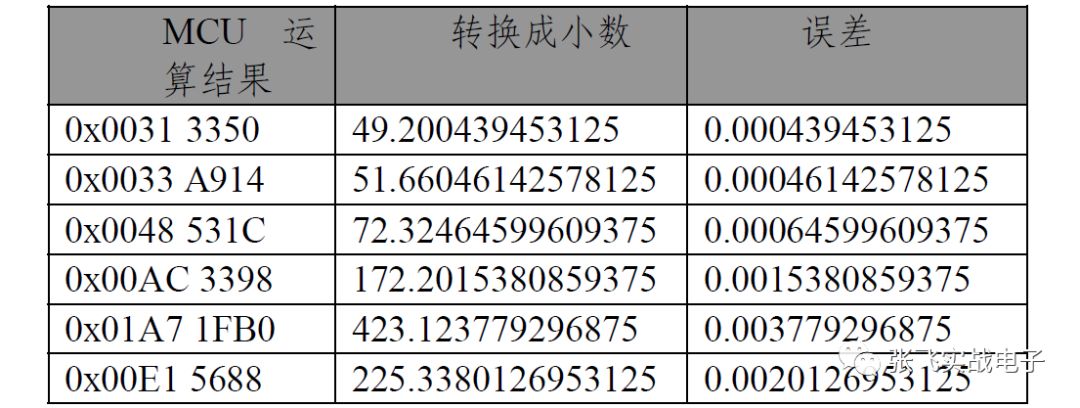
如果運算不需要小數部分（即運算結果取整），則"MCU 運算結果"中的數值均需要向右移動16位去掉小數部分；在代碼中，用戶可以直接取MR1的數字做為整數結果（假如不考慮四舍五入）。