編者按:機器學習開放課程第七課,Snap軟件工程師Sergey Korolev講解了主成分分析降維方法和常用聚類方法。
對CIFAR-10應用t-SNE可視化技術(L2距離)
歡迎來到開放機器學習課程的第七課!
在這節課中,我們將討論主成分分析(PCA)和聚類(clustering)這樣的無監督學習方法。你將學習為何以及如何降低原始數據的維度,還有分組類似數據點的主要方法。
概覽
介紹
主成分分析
直覺、理論、應用問題
用例
聚類分析
K均值
近鄰傳播
譜聚類
凝聚聚類
精確性測度
作業七
相關資源
介紹
和分類、回歸方法相比,無監督學習算法的主要特性是輸入數據是未標注過的(即沒有給定的標簽或分類),算法在沒有任何鋪助的條件下學習數據的結構。這帶來了兩點主要不同。首先,它讓我們可以處理大量數據,因為數據不需要人工標注。其次,評估無監督算法的質量比較難,因為缺乏監督學習所用的明確的優秀測度。
無監督學習中最常見的任務之一是降維。一方面,降維可能有助于可視化數據(例如,t-SNE方法);另一方面,它可能有助于處理數據的多重共線性,為監督學習方法(例如,決策樹)準備數據。
主成分分析
直覺、理論、應用問題
主成分分析是最簡單、最直觀、最頻繁使用的降維方法之一,投射數據至其正交特征子空間。
更一般地說,所有觀測可以被看成位于初始特征空間的一個子空間上的橢圓,該子空間的新基底與橢圓軸對齊。這一假定讓我們移除高度相關的特征,因為基底向量是正交的。在一般情況下,所得橢圓的維度和初始空間的維度相當,但假定數據位于一個維度較小的子空間讓我們可以在新投影(子空間)上移除“過多的”空間。我們以“貪婪”方式達成這一點,通過識別散度最大之處循序選擇每個橢圓軸。
讓我們看下這一過程的數學:
為了將數據的維度從n降至k(k <= n),我們以散度降序給軸列表排序,并移除其中最大的k項。
我們從計算初始特征的散度和協方差開始。這通常基于協方差矩陣達成。根據協方差的定義,兩項特征的協方差據下式計算:
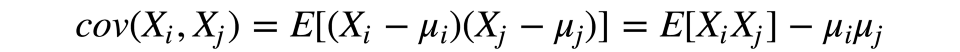
其中,μ是第i項特征的期望值。值得注意的是,協方差是對稱的,一個向量自身的協方差等于其散度。
因此,在對角特征的散度上,協方差是對稱的。非對角值為相應特征對的協方差。若X是觀測的矩陣,則協方差矩陣為:
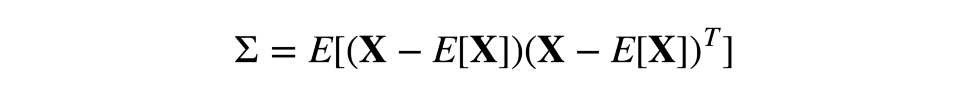
快速溫習:作為線性操作的矩陣,有本征值和本征向量。它們非常方便,因為它們描述了我們的空間在應用線性操作時不會翻轉只會拉伸的部分;本征向量保持相同的方向,但是根據相應的本征值拉伸。形式化地說,矩陣M、本征向量w、本征值λ滿足如下等式:
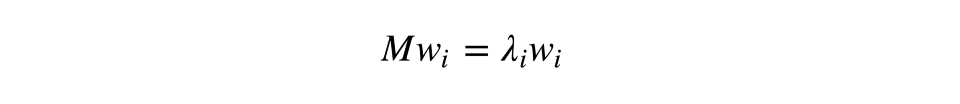
樣本X的協方差矩陣可以寫成轉置矩陣X和X自身的乘積。據Rayleigh quotient,樣本的最大差異沿該矩陣的本征向量分布,且和最大本征值相一致。因此,我們打算保留的數據主成分不過是對應矩陣的k個最大本征值的本征向量。
下面的步驟要容易理解一點。我們將數據X矩陣乘以其成分,以得到我們的數據在選中的成分的正交基底上的投影。如果成分的數目小于初始空間維數,記住我們在應用這一轉換的過程中會丟失一點信息。
用例
讓我們看兩個例子。
iris數據集
首先我們先來查看下iris樣本:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set(style='white')
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
from sklearn import decomposition
from sklearn import datasets
from mpl_toolkits.mplot3d importAxes3D
# 加載數據集
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 創建美觀的3D圖
fig = plt.figure(1, figsize=(6, 5))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla()
for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 0].mean(),
X[y == label, 1].mean() + 1.5,
X[y == label, 2].mean(), name,
horizontalalignment='center',
bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
# 變動標簽的順序
y_clr = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y_clr, cmap=plt.cm.spectral)
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([]);
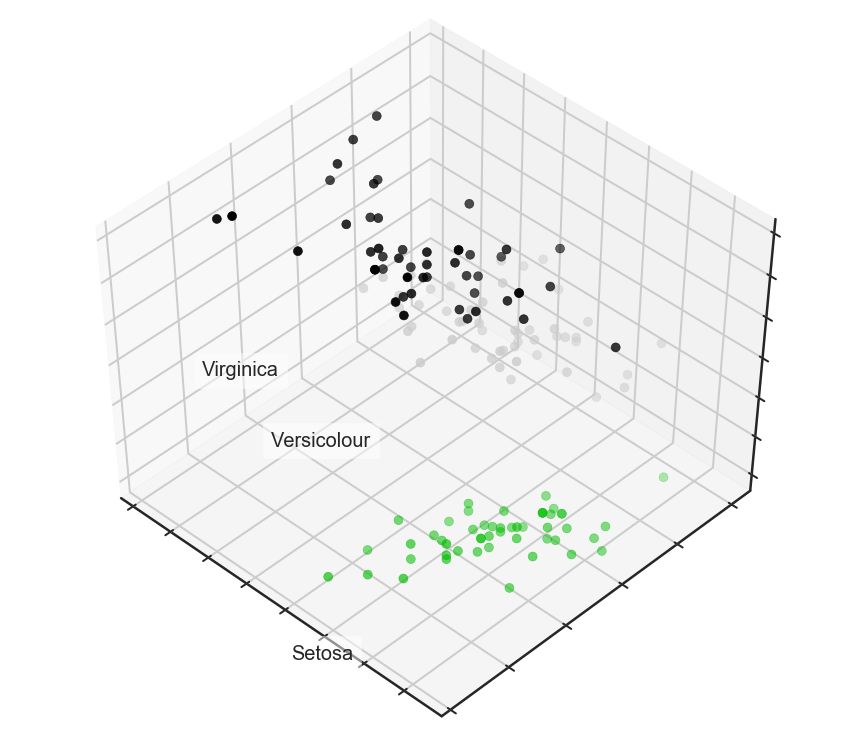
下面讓我們看看PCA將如何提高一個不能很好地擬合所有訓練數據的簡單模型的結果:
from sklearn.tree importDecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, roc_auc_score
# 切分訓練集、測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3,
stratify=y,
random_state=42)
# 深度為2的決策樹
clf = DecisionTreeClassifier(max_depth=2, random_state=42)
clf.fit(X_train, y_train)
preds = clf.predict_proba(X_test)
print('Accuracy: {:.5f}'.format(accuracy_score(y_test,
preds.argmax(axis=1))))
Accuracy: 0.88889
讓我們再試一次,不過這回我們將把維數降到2:
# 使用sklearn提供的PCA
pca = decomposition.PCA(n_components=2)
X_centered = X - X.mean(axis=0)
pca.fit(X_centered)
X_pca = pca.transform(X_centered)
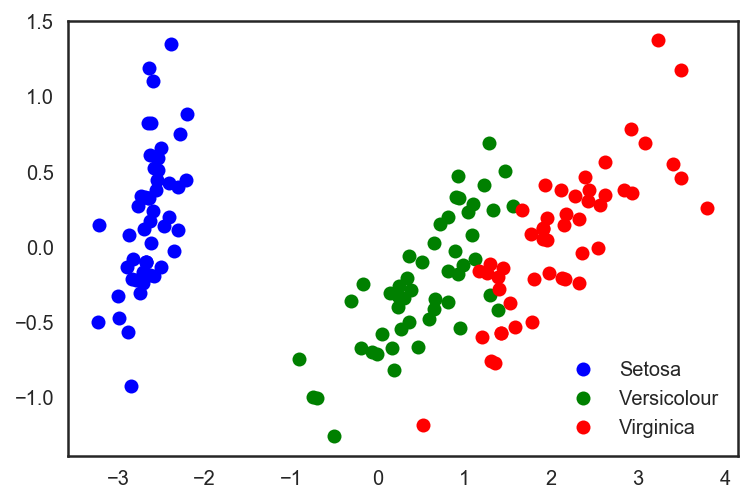
# 繪制PCA結果
plt.plot(X_pca[y == 0, 0], X_pca[y == 0, 1], 'bo', label='Setosa')
plt.plot(X_pca[y == 1, 0], X_pca[y == 1, 1], 'go', label='Versicolour')
plt.plot(X_pca[y == 2, 0], X_pca[y == 2, 1], 'ro', label='Virginica')
plt.legend(loc=0);
# 分割測試集、訓練集,同時應用PCA
X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=.3,
stratify=y,
random_state=42)
clf = DecisionTreeClassifier(max_depth=2, random_state=42)
clf.fit(X_train, y_train)
preds = clf.predict_proba(X_test)
print('Accuracy: {:.5f}'.format(accuracy_score(y_test,
preds.argmax(axis=1))))
Accuracy: 0.91111
在這個例子中,精確度的增加并不明顯。但對其他高維數據集而言,PCA可以戲劇性地提升決策樹和其他集成方法的精確度。
現在,讓我們查看下可以通過每個選中成分解釋的方差百分比。
for i, component in enumerate(pca.components_):
print("{} component: {}% of initial variance".format(i + 1,
round(100 * pca.explained_variance_ratio_[i], 2)))
print(" + ".join("%.3f x %s" % (value, name)
for value, name in zip(component,
iris.feature_names)))
1 component: 92.46% of initial variance 0.362 x sepal length (cm) + -0.082 x sepal width (cm) + 0.857 x petal length (cm) + 0.359 x petal width (cm)
2 component: 5.3% of initial variance 0.657 x sepal length (cm) + 0.730 x sepal width (cm) + -0.176 x petal length (cm) + -0.075 x petal width (cm)
手寫數字數據集
讓我們看下之前在第3課中用過的手寫數字數據集。
digits = datasets.load_digits()
X = digits.data
y = digits.target
讓我們從可視化數據開始。獲取前10個數字。我們使用由每個像素的亮度值構成的8x8矩陣表示數字。每個矩陣壓扁至由64個數字構成的向量,這樣我們就得到了數據的特征版本。
# f, axes = plt.subplots(5, 2, sharey=True, figsize=(16,6))
plt.figure(figsize=(16, 6))
for i in range(10):
plt.subplot(2, 5, i + 1)
plt.imshow(X[i,:].reshape([8,8]), cmap='gray');
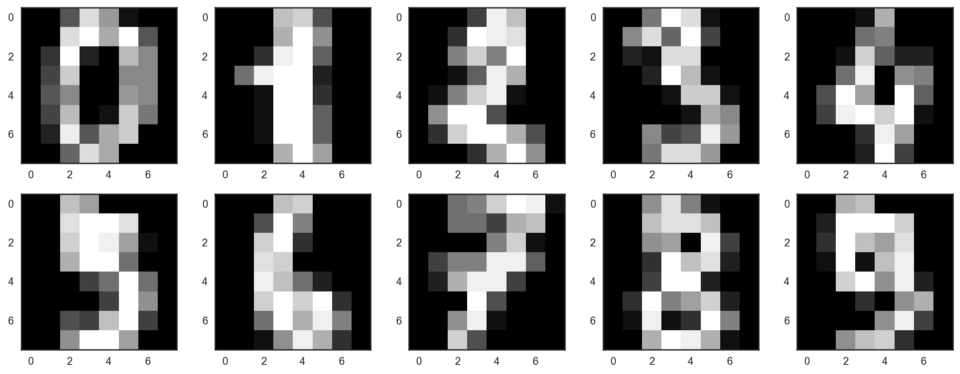
我們的數據有64個維度,不過我們將降維至2維。我們將看到,即使僅有2個維度,我們也可以清楚地看到數字分離為聚類。
pca = decomposition.PCA(n_components=2)
X_reduced = pca.fit_transform(X)
plt.figure(figsize=(12,10))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y,
edgecolor='none', alpha=0.7, s=40,
cmap=plt.cm.get_cmap('nipy_spectral', 10))
plt.colorbar()
plt.title('MNIST. PCA projection');
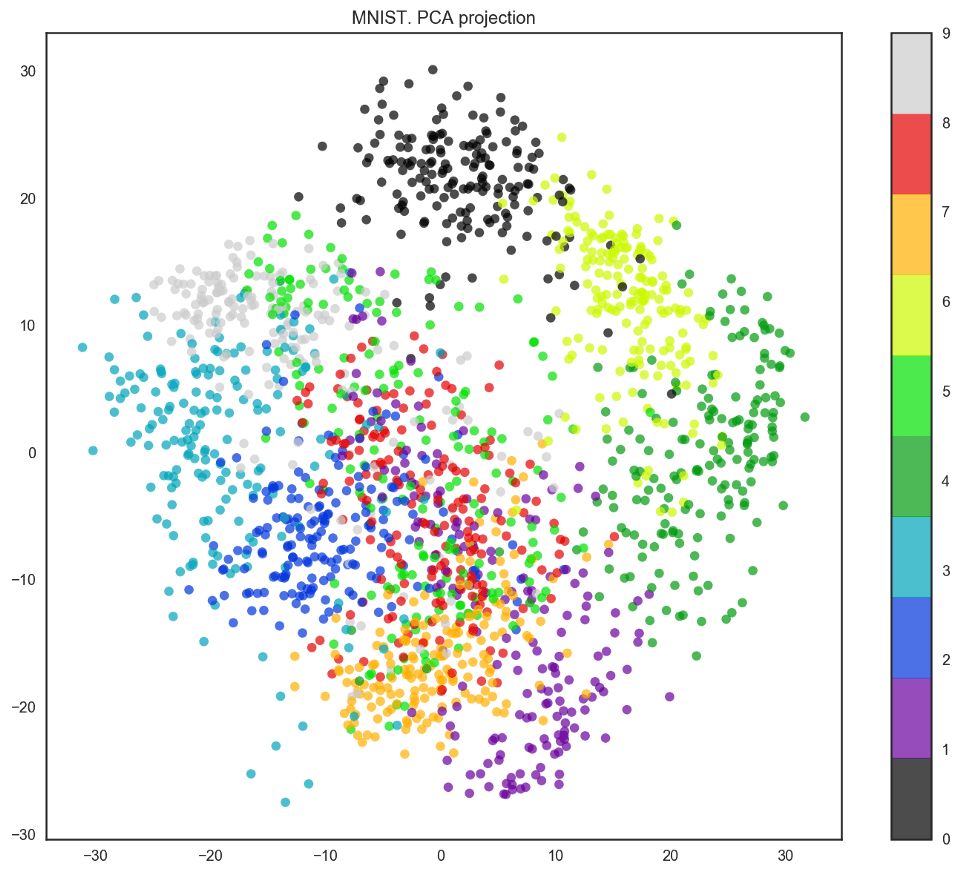
事實上,t-SNE的效果要更好,因為PCA有線性限制,而t-SNE沒有。然而,即使在這樣一個小數據集上,t-SNE算法的計算時間也明顯高于PCA。
from sklearn.manifold import TSNE
tsne = TSNE(random_state=17)
X_tsne = tsne.fit_transform(X)
plt.figure(figsize=(12,10))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y,
edgecolor='none', alpha=0.7, s=40,
cmap=plt.cm.get_cmap('nipy_spectral', 10))
plt.colorbar()
plt.title('MNIST. t-SNE projection');
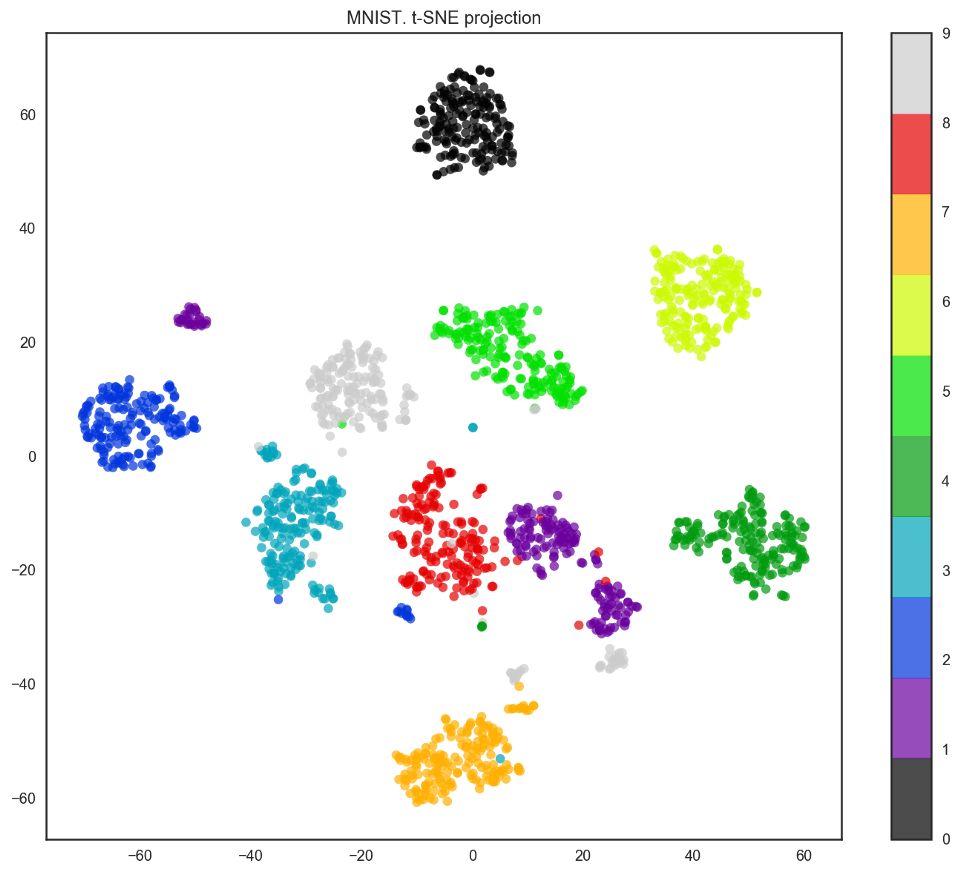
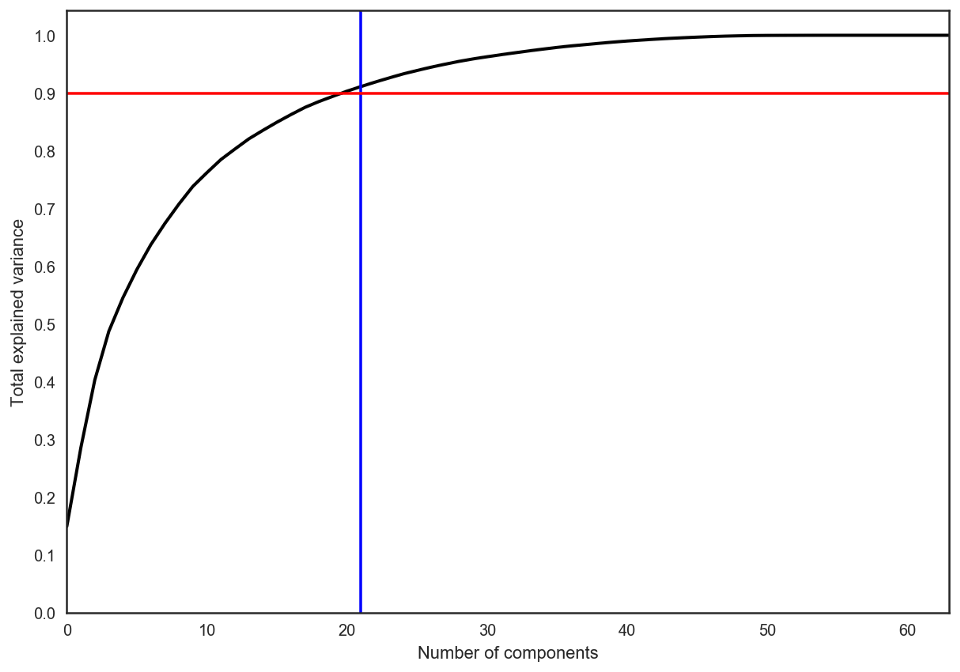
在實踐中,我們選擇的主成分數目會滿足我們可以解釋90%的初始數據散度(通過explained_variance_ratio)。在這里,這意味著我們將保留21個主成分;因此,我們將維度從64降至21.
pca = decomposition.PCA().fit(X)
plt.figure(figsize=(10,7))
plt.plot(np.cumsum(pca.explained_variance_ratio_), color='k', lw=2)
plt.xlabel('Number of components')
plt.ylabel('Total explained variance')
plt.xlim(0, 63)
plt.yticks(np.arange(0, 1.1, 0.1))
plt.axvline(21, c='b')
plt.axhline(0.9, c='r')
plt.show();
聚類
聚類背后的主要思路相當直截了當。基本上,我們這樣對自己說:“我這里有這些數據點,并且我們可以看到它們的分組。如果能更具體地描述這些就好了,同時,當出現新數據點時,將它分配給正確的分組。”這個通用的想法鼓勵探索多種多樣的聚類算法。
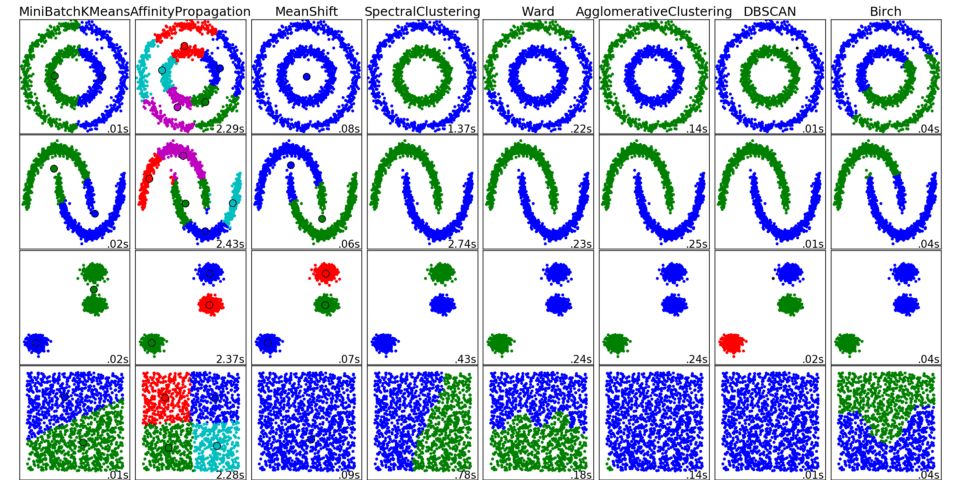
scikit-learn中的不同聚類算法的結果
下面列出的算法沒有覆蓋所有聚類方法,但它們是最常用的聚類方法。
K均值
在所有聚類算法中,K均值是最流行的,也是最簡單的。它的基本步驟為:
選定你認為最優的聚類數k。
在數據空間中隨機初始化k點作為“中心點”。
將每個觀測分配至最近的中心點。
將中心點更新為所有分配至同一中心點的觀測的中心。
重復第3、4步,重復固定次數,或直到所有中心點穩定下來(即在第4步中沒有變化)。
這一算法很容易描述和可視化。
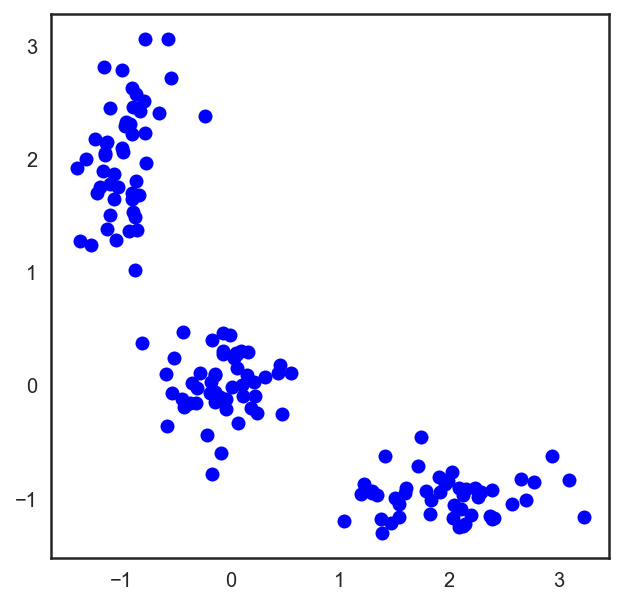
# 讓我們從分配3個聚類的點開始。
X = np.zeros((150, 2))
np.random.seed(seed=42)
X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50)
X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50)
X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50)
X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50)
plt.figure(figsize=(5, 5))
plt.plot(X[:, 0], X[:, 1], 'bo');
# Scipy有一個函數,接受2個元組,返回兩者之間的距離
from scipy.spatial.distance import cdist
# 隨機分配3個中心點
np.random.seed(seed=42)
centroids = np.random.normal(loc=0.0, scale=1., size=6)
centroids = centroids.reshape((3, 2))
cent_history = []
cent_history.append(centroids)
for i in range(3):
# 計算數據點至中心點的距離
distances = cdist(X, centroids)
# 檢查哪個是最近的中心點
labels = distances.argmin(axis=1)
# 根據點的距離標記數據點
centroids = centroids.copy()
centroids[0, :] = np.mean(X[labels == 0, :], axis=0)
centroids[1, :] = np.mean(X[labels == 1, :], axis=0)
centroids[2, :] = np.mean(X[labels == 2, :], axis=0)
cent_history.append(centroids)
# 讓我們繪制K均值步驟
plt.figure(figsize=(8, 8))
for i in range(4):
distances = cdist(X, cent_history[i])
labels = distances.argmin(axis=1)
plt.subplot(2, 2, i + 1)
plt.plot(X[labels == 0, 0], X[labels == 0, 1], 'bo', label='cluster #1')
plt.plot(X[labels == 1, 0], X[labels == 1, 1], 'co', label='cluster #2')
plt.plot(X[labels == 2, 0], X[labels == 2, 1], 'mo', label='cluster #3')
plt.plot(cent_history[i][:, 0], cent_history[i][:, 1], 'rX')
plt.legend(loc=0)
plt.title('Step {:}'.format(i + 1));

這里,我們使用了歐幾里得距離,不過算法可以通過任何其他測度收斂。你不僅可以改動步驟的數目,或者收斂標準,還可以改動數據點和聚類中心點之間的距離衡量方法。
這一算法的另一項“特性”是,它對聚類中心點的初始位置敏感。你可以多次運行該算法,接著平均所有中心點結果。
選擇K均值的聚類數
和分類、回歸之類的監督學習任務不同,聚類需要花更多心思在選擇優化標準上。使用K均值時,我們通常優化觀測及其中心點的平方距離之和。
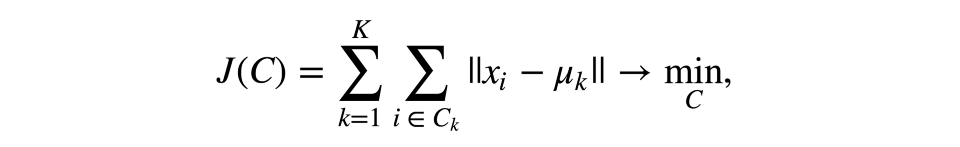
其中C為冪為K的聚類集合,μ為聚類中心點。
這個定義看起來很合理——我們想要觀測盡可能地接近其中心點。但是,這里有一個問題——當中心點的數量等于觀測的數量時,將達到最優值,所以最終你得到的每個觀測自成一個聚類。
為了避免這一情形,我們應該選擇聚類數,使這一數字之后的函數J(C)下降得不那么快。形式化一點來說:
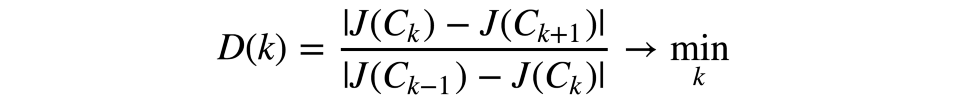
讓我們來看一個例子。
from sklearn.cluster importKMeans
inertia = []
for k in range(1, 8):
kmeans = KMeans(n_clusters=k, random_state=1).fit(X)
inertia.append(np.sqrt(kmeans.inertia_))
plt.plot(range(1, 8), inertia, marker='s');
plt.xlabel('$k$')
plt.ylabel('$J(C_k)$');
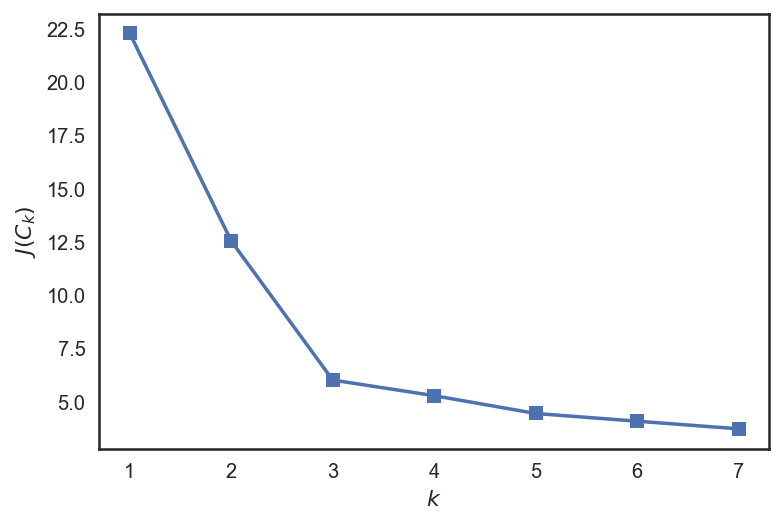
我們可以看到,J(C)在3之前下降得很快,在此之后變化不大。這意味著,聚類的最佳數字是3.
問題
K均值內在地是NP-hard的。對d維、k聚類、n觀測而言,算法復雜度為O(n(dk+1))。有一些啟發式的算法可以緩解這一問題;例如MiniBatch K均值,分批次處理數據,而不是一下子擬合整個數據集,接著通過對之前的步驟取平均數移動中心點。
scikit-learn的實現有一些優勢,例如可以使用n_init函數參數聲明初始化數,讓我們識別更有魯棒性的中心點。此外,算法可以并行運行,以減少計算時間。
近鄰傳播
近鄰傳播是聚類算法的另一個例子。和K均值不同,這一方法不需要我們事先設定聚類的數目。這一算法的主要思路是我們將根據觀測的相似性(或者說,它們“符合”彼此的程度)聚類數據。
讓我們定義一種相似性測度,對觀測x、y、z而言,若x更接近y,而非z,那么s(x, y) > s(x, z)。s的一個簡單例子是負平方距離s(x, y) = - ||x-y||2。
現在讓我們通過兩個矩陣來描述“相符程度”。其中一個矩陣ri,k將決定,相比七塔寺所有可能的“角色模型”,第k個觀測是第i個觀測的“角色模型”的合適程度。另一個矩陣ai,k將決定,第i個觀測選擇第k個觀測作為“角色模型”的合適程度。這可能聽起來有點困惑,但如果你自己想一個例子實際操作一下,就要好理解得多。
矩陣根據如下規則依次更新:
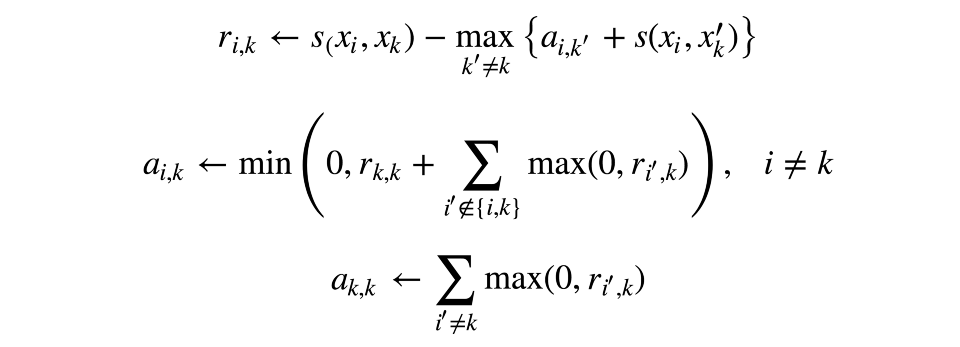
譜聚類
譜聚類組合了上面描述過的一些方法,創建了一種更強勁的聚類方法。
首先,該算法需要我們定義觀測的相似性矩陣——鄰接矩陣。這一步可以使用和近鄰傳播類似的方法做到,所以矩陣A將儲存相應數據點之間的負平方距離。該矩陣描繪了一整張圖,其中觀測為頂點,每對觀測之間的估計相似值為這對頂點間的邊。就上面定義的測度和二維觀測而言,這是相當直觀的——如果兩個觀測之間的邊最短,那么這兩個觀測相似。我們將把圖分割為兩張子圖,滿足以下條件:每張子圖中的每個觀測和這張子圖中的另一個觀測相似。形式化地說,這是一個Normalized cuts問題;建議閱讀以下論文了解具體細節:
http://people.eecs.berkeley.edu/%7Emalik/papers/SM-ncut.pdf
凝聚聚類
在不使用固定聚類數目的聚類算法中,該算法是最簡單、最容易理解的。
這一算法相當簡單:
剛開始,每個觀測自成其聚類
根據聚類中心兩兩距離降序排列
合并最近的兩個相鄰聚類,然后重新計算中心
重復第2、3步直到所有數據合并為一個聚類
搜索最近聚類有多種方法:
單鏈(Single linkage)
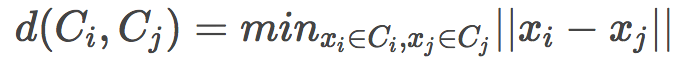
全鏈(Complete linkage)
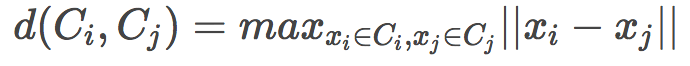
平均鏈(Average linkage)
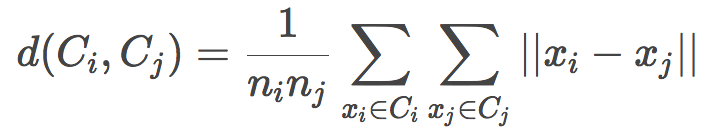
中心鏈(Centroid linkage)
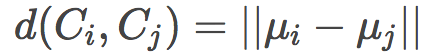
其中,第三個方法是最有效率的做法,因為它不需要在每次聚類合并后重新計算距離。
凝聚聚類的結果可以可視化為美觀的聚類樹(樹枝形結構聯系圖),幫助識別算法應該停止的時刻,以得到最有結果。有很多Python工具可以構建這樣的樹枝形結構聯系圖。
讓我們考慮之前的K均值聚類一節中所用的例子:
from scipy.cluster import hierarchy
from scipy.spatial.distance import pdist
X = np.zeros((150, 2))
np.random.seed(seed=42)
X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50)
X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50)
X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50)
X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50)
distance_mat = pdist(X) # pdist計算上三角距離矩陣
Z = hierarchy.linkage(distance_mat, 'single') # linkage為凝聚聚類算法
plt.figure(figsize=(10, 5))
dn = hierarchy.dendrogram(Z, color_threshold=0.5)
精確性測度
和分類相反,很難評估聚類所得結果的質量。這里,測度無法依賴于標簽,只能取決于分割的質量。其次,當我們進行聚類時,我們通常不具備觀測的真實標簽。
質量測度分為內、外部。外部測度使用關于已知真實分割的信息,而內部測度不使用任何外部信息,僅基于初始數據評估聚類的質量。聚類的最優數目通常根據某些內部測度決定。
所有下面的測度都包含在sklearn.metrics中。
調整蘭德指數(ARI)
這里,我們假定目標的真實標簽是已知的。令N為樣本中的觀測數,a為標簽相同、位于同一聚類中的觀測對數,b為標簽不同、位于不同聚類中的觀測數。蘭德指數可由下式得出:
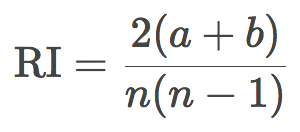
換句話說,蘭德指數評估分割后的聚類結果和初始標簽一致的比例。為了讓任意觀測數、聚類數的蘭德指數接近零,我們有必要縮放其大小,由此得到了調整蘭德指數:
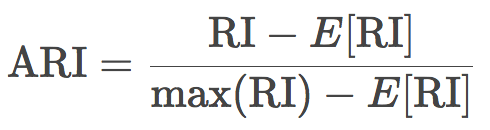
這一測度是對稱的,不受標簽排列的影響。因此,該指數是不同樣本分割距離的衡量。ARI的取值范圍是[-1, 1],負值意味著分割更獨立,正值意味著分割更一致(ARI = 1意味著分割完全一致)。
調整互信息(AMI)
這一測度和ARI相似。它也是對稱的,不受標簽的具體值及排列的影響。它由熵函數定義,將樣本分割視作離散分布。MI指數定義為兩個分布的互信息,這兩個分布對應于樣本分割聚類。直觀地說,互信息衡量兩個聚類分割共享的信息量,即,關于其中之一的信息在多大程度上可以降低另一個的不確定性。
AMI的定義方式和ARI類似。這讓我們可以避免因聚類數增長而導致的MI指數增長。AMI的取值范圍為[0, 1]。接近零意味著分割更獨立,接近1意味著分割更相似(AMI = 1意味著完全一致)。
同質性、完整性、V-measure
形式化地說,這些測度同樣基于熵函數和條件熵函數定義,將樣本分割視作離散分布:
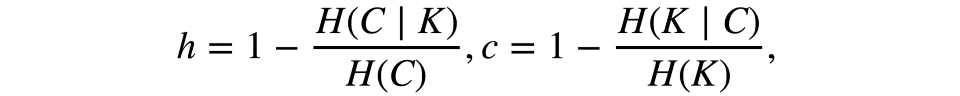
其中K為聚類結果,C為初始分割。因此,h評估是否每個聚類由相同分類目標組成,而c評估相同分類買的物品分屬聚類的匹配程度。這些測度不是對稱的。兩者的取值范圍均為[0, 1],接近1的值暗示更精確的聚類結果。這些測度的值不像ARI或AMI一樣縮放過,因此取決于聚類數。當一個隨機聚類結果的聚類數足夠大,而目標數足夠小時,這一測度的值不會接近零。在這樣的情形下,使用ARI要更合理。然而,當觀測數大于100而聚類數小于10時,這一問題并不致命,可以忽略。
V-measure結合了h和c,為h和c的調和平均數:v = (2hc)/(h + c)。它是對稱的,衡量兩個聚類結果的一致性。
輪廓
和之前描述的測度都不一樣,輪廓系數(silhouette coefficient)無需目標真實標簽的知識。它讓我們僅僅根據未標注的初始樣本和聚類結果估計聚類的質量。首先,為每項觀測計算輪廓系數。令a為某目標到同一聚類中的其他目標的平均距離,又令b為該目標到最近聚類(不同于該目標所屬聚類)中的目標的平均距離,則該目標的輪廓系數為:
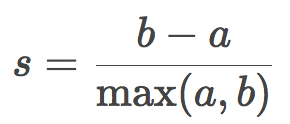
樣本的輪廓系數為樣本中所有數據點的輪廓系數的均值。該系數的取值范圍為[-1, 1],輪廓系數越高,意味著聚類的結果越好。
輪廓系數有助于確定聚類數k的最佳值:選取最大化輪廓系數的聚類數。
作為總結,讓我們看看這些測度在MNIST手寫數字數據集上的效果如何:
from sklearn import metrics
from sklearn import datasets
import pandas as pd
from sklearn.cluster importKMeans, AgglomerativeClustering, AffinityPropagation, SpectralClustering
data = datasets.load_digits()
X, y = data.data, data.target
algorithms = []
algorithms.append(KMeans(n_clusters=10, random_state=1))
algorithms.append(AffinityPropagation())
algorithms.append(SpectralClustering(n_clusters=10, random_state=1,
affinity='nearest_neighbors'))
algorithms.append(AgglomerativeClustering(n_clusters=10))
data = []
for algo in algorithms:
algo.fit(X)
data.append(({
'ARI': metrics.adjusted_rand_score(y, algo.labels_),
'AMI': metrics.adjusted_mutual_info_score(y, algo.labels_),
'Homogenity': metrics.homogeneity_score(y, algo.labels_),
'Completeness': metrics.completeness_score(y, algo.labels_),
'V-measure': metrics.v_measure_score(y, algo.labels_),
'Silhouette': metrics.silhouette_score(X, algo.labels_)}))
results = pd.DataFrame(data=data, columns=['ARI', 'AMI', 'Homogenity',
'Completeness', 'V-measure',
'Silhouette'],
index=['K-means', 'Affinity',
'Spectral', 'Agglomerative'])
results
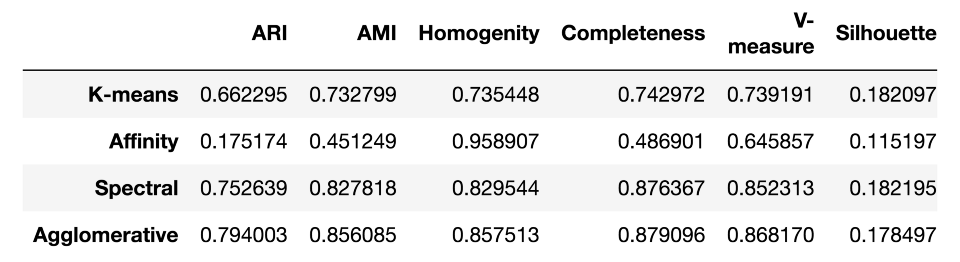
-
聚類
+關注
關注
0文章
146瀏覽量
14212 -
降維
+關注
關注
0文章
10瀏覽量
7643 -
機器學習
+關注
關注
66文章
8406瀏覽量
132567
原文標題:機器學習開放課程(七):無監督學習:PCA和聚類
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于Contourlet變換和主成分分析的高光譜數據噪聲消除
主成分分析的圖像壓縮與重構
改進主成分分析貝葉斯判別方法
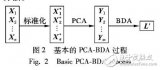




 主成分分析降維方法和常用聚類方法
主成分分析降維方法和常用聚類方法










評論