1、FFM理論
在CTR預估中,經常會遇到one-hot類型的變量,one-hot類型變量會導致嚴重的數據特征稀疏的情況,為了解決這一問題,在上一講中,我們介紹了FM算法。這一講我們介紹一種在FM基礎上發展出來的算法-FFM(Field-aware Factorization Machine)。
FFM模型中引入了類別的概念,即field。還是拿上一講中的數據來講,先看下圖:
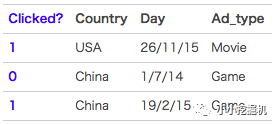
在上面的廣告點擊案例中,
“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”這三個特征都是代表日期的,可以放到同一個field中。同理,Country也可以放到一個field中。簡單來說,同一個categorical特征經過One-Hot編碼生成的數值特征都可以放到同一個field,包括用戶國籍,廣告類型,日期等等。
在FFM中,每一維特征 xi,針對其它特征的每一種field fj,都會學習一個隱向量 v_i,fj。因此,隱向量不僅與特征相關,也與field相關。也就是說,“Day=26/11/15”這個特征與“Country”特征和“Ad_type"特征進行關聯的時候使用不同的隱向量,這與“Country”和“Ad_type”的內在差異相符,也是FFM中“field-aware”的由來。
假設樣本的 n個特征屬于 f個field,那么FFM的二次項有 nf個隱向量。而在FM模型中,每一維特征的隱向量只有一個。FM可以看作FFM的特例,是把所有特征都歸屬到一個field時的FFM模型。根據FFM的field敏感特性,可以導出其模型方程。
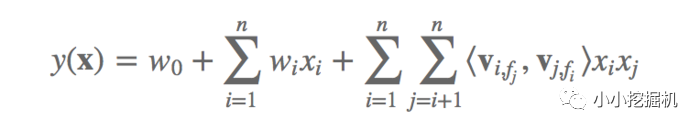
可以看到,如果隱向量的長度為 k,那么FFM的二次參數有 nfk 個,遠多于FM模型的 nk個。此外,由于隱向量與field相關,FFM二次項并不能夠化簡,其預測復雜度是 O(kn^2)。
下面以一個例子簡單說明FFM的特征組合方式。輸入記錄如下:

這條記錄可以編碼成5個特征,其中“Genre=Comedy”和“Genre=Drama”屬于同一個field,“Price”是數值型,不用One-Hot編碼轉換。為了方便說明FFM的樣本格式,我們將所有的特征和對應的field映射成整數編號。
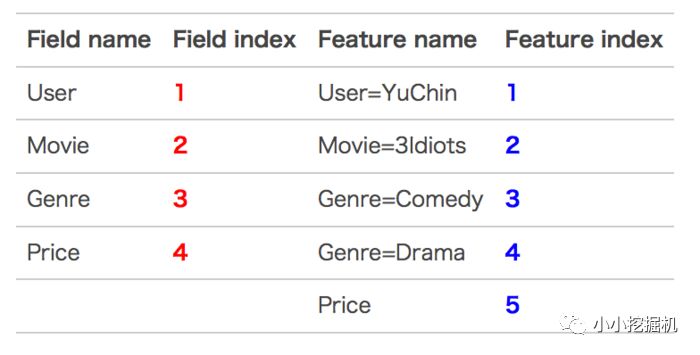
那么,FFM的組合特征有10項,如下圖所示。

其中,紅色是field編號,藍色是特征編號。
2、FFM實現細節
這里講得只是一種FFM的實現方式,并不是唯一的。
損失函數
FFM將問題定義為分類問題,使用的是logistic loss,同時加入了正則項
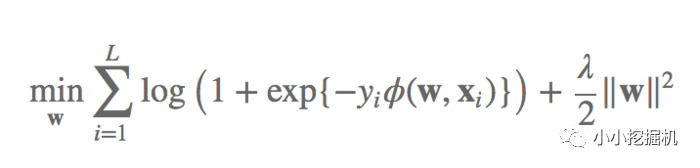
什么,這是logisitc loss?第一眼看到我是懵逼的,邏輯回歸的損失函數我很熟悉啊,不是長這樣的啊?其實是我目光太短淺了。邏輯回歸其實是有兩種表述方式的損失函數的,取決于你將類別定義為0和1還是1和-1。大家可以參考下下面的文章:https://www.cnblogs.com/ljygoodgoodstudydaydayup/p/6340129.html。當我們將類別設定為1和-1的時候,邏輯回歸的損失函數就是上面的樣子。
隨機梯度下降
訓練FFM使用的是隨機梯度下降方法,即每次只選一條數據進行訓練,這里還有必要補一補梯度下降的知識,梯度下降是有三種方式的,截圖取自參考文獻3:
總給人一種怪怪的感覺。batch為什么是全量的數據呢,哈哈。
3、tensorflow實現代碼
本文代碼的github地址:https://github.com/princewen/tensorflow_practice/tree/master/recommendation-FFM-Demo
這里我們只講解一些細節,具體的代碼大家可以去github上看:
生成數據這里我沒有找到合適的數據,就自己產生了一點數據,數據涉及20維特征,前十維特征是一個field,后十維是一個field:
def gen_data(): labels = [-1,1] y = [np.random.choice(labels,1)[0] for _ in range(all_data_size)] x_field = [i // 10 for i in range(input_x_size)] x = np.random.randint(0,2,size=(all_data_size,input_x_size)) return x,y,x_field
定義權重項在ffm中,有三個權重項,首先是bias,然后是一維特征的權重,最后是交叉特征的權重:
def createTwoDimensionWeight(input_x_size,field_size,vector_dimension): weights = tf.truncated_normal([input_x_size,field_size,vector_dimension]) tf_weights = tf.Variable(weights) return tf_weights def createOneDimensionWeight(input_x_size): weights = tf.truncated_normal([input_x_size]) tf_weights = tf.Variable(weights) return tf_weights def createZeroDimensionWeight(): weights = tf.truncated_normal([1]) tf_weights = tf.Variable(weights) return tf_weights
計算估計值估計值的計算這里不能項FM一樣先將公式化簡再來做,對于交叉特征,只能寫兩重循環,所以對于特別多的特征的情況下,真的計算要爆炸呀!
def inference(input_x,input_x_field,zeroWeights,oneDimWeights,thirdWeight): """計算回歸模型輸出的值""" secondValue = tf.reduce_sum(tf.multiply(oneDimWeights,input_x,name='secondValue')) firstTwoValue = tf.add(zeroWeights, secondValue, name="firstTwoValue") thirdValue = tf.Variable(0.0,dtype=tf.float32) input_shape = input_x_size for i in range(input_shape): featureIndex1 = I fieldIndex1 = int(input_x_field[I]) for j in range(i+1,input_shape): featureIndex2 = j fieldIndex2 = int(input_x_field[j]) vectorLeft = tf.convert_to_tensor([[featureIndex1,fieldIndex2,i] for i in range(vector_dimension)]) weightLeft = tf.gather_nd(thirdWeight,vectorLeft) weightLeftAfterCut = tf.squeeze(weightLeft) vectorRight = tf.convert_to_tensor([[featureIndex2,fieldIndex1,i] for i in range(vector_dimension)]) weightRight = tf.gather_nd(thirdWeight,vectorRight) weightRightAfterCut = tf.squeeze(weightRight) tempValue = tf.reduce_sum(tf.multiply(weightLeftAfterCut,weightRightAfterCut)) indices2 = [I] indices3 = [j] xi = tf.squeeze(tf.gather_nd(input_x, indices2)) xj = tf.squeeze(tf.gather_nd(input_x, indices3)) product = tf.reduce_sum(tf.multiply(xi, xj)) secondItemVal = tf.multiply(tempValue, product) tf.assign(thirdValue, tf.add(thirdValue, secondItemVal)) return tf.add(firstTwoValue,thirdValue)
定義損失函數損失函數我們就用邏輯回歸損失函數來算,同時加入正則項:
lambda_w = tf.constant(0.001, name='lambda_w') lambda_v = tf.constant(0.001, name='lambda_v') zeroWeights = createZeroDimensionWeight() oneDimWeights = createOneDimensionWeight(input_x_size) thirdWeight = createTwoDimensionWeight(input_x_size, # 創建二次項的權重變量 field_size, vector_dimension) # n * f * k y_ = inference(input_x, trainx_field,zeroWeights,oneDimWeights,thirdWeight) l2_norm = tf.reduce_sum( tf.add( tf.multiply(lambda_w, tf.pow(oneDimWeights, 2)), tf.reduce_sum(tf.multiply(lambda_v, tf.pow(thirdWeight, 2)),axis=[1,2]) ) ) loss = tf.log(1 + tf.exp(input_y * y_)) + l2_norm train_step = tf.train.GradientDescentOptimizer(learning_rate=lr).minimize(loss)
訓練接下來就是訓練了,每次只用喂一個數據就好:
input_x_batch = trainx[t] input_y_batch = trainy[t] predict_loss,_, steps = sess.run([loss,train_step, global_step], feed_dict={input_x: input_x_batch, input_y: input_y_batch})
跑的是相當的慢,我們來看看效果吧:
-
編碼
+關注
關注
6文章
946瀏覽量
54869 -
函數
+關注
關注
3文章
4338瀏覽量
62734 -
代碼
+關注
關注
30文章
4799瀏覽量
68728
原文標題:推薦系統遇上深度學習(二)--FFM模型理論和實踐
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
D類放大器原理及EMI抑制
UCC28600準諧振反激節制IC 引腳功能
分立器件的實現的細節
FM和FFM原理的探索和應用的經驗
現階段對尾氣的處理方法
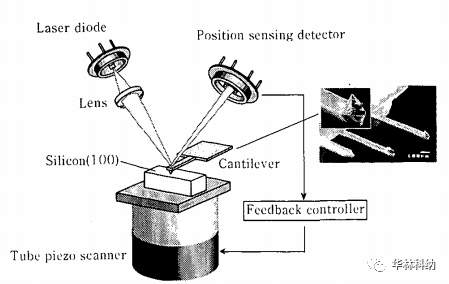
利用FFM機制進行的極微細機械加工
華為EUV光刻解決相干光無法勻光問題
ATV 320同步與異步電機變頻器編程手冊
大模型部署框架FastLLM實現細節解析





 FFM理論與FFM實現細節
FFM理論與FFM實現細節











評論