1、決策樹模型與學(xué)習(xí)
決策樹(decision tree)算法基于特征屬性進(jìn)行分類,其主要的優(yōu)點:模型具有可讀性,計算量小,分類速度快。決策樹算法包括了由Quinlan提出的ID3與C4.5,Breiman等提出的CART。其中,C4.5是基于ID3的,對分裂屬性的目標(biāo)函數(shù)做出了改進(jìn)。
決策樹模型
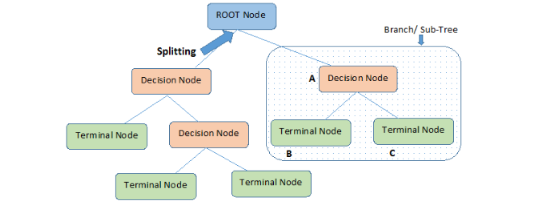
決策樹是一種通過對特征屬性的分類對樣本進(jìn)行分類的樹形結(jié)構(gòu),包括有向邊與三類節(jié)點:
根節(jié)點(root node),表示第一個特征屬性,只有出邊沒有入邊;
內(nèi)部節(jié)點(internal node),表示特征屬性,有一條入邊至少兩條出邊
葉子節(jié)點(leaf node),表示類別,只有一條入邊沒有出邊。
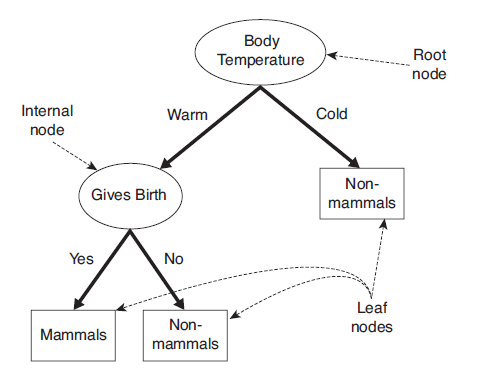
上圖給出了(二叉)決策樹的示例。決策樹具有以下特點:
對于二叉決策樹而言,可以看作是if-then規(guī)則集合,由決策樹的根節(jié)點到葉子節(jié)點對應(yīng)于一條分類規(guī)則;
分類規(guī)則是互斥并且完備的,所謂互斥即每一條樣本記錄不會同時匹配上兩條分類規(guī)則,所謂完備即每條樣本記錄都在決策樹中都能匹配上一條規(guī)則。
分類的本質(zhì)是對特征空間的劃分,如下圖所示,
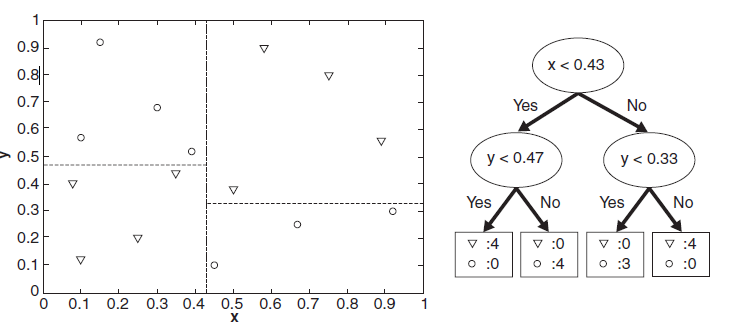
決策樹學(xué)習(xí)
決策樹學(xué)習(xí)的本質(zhì)是從訓(xùn)練數(shù)據(jù)集中歸納出一組分類規(guī)則[2]。但隨著分裂屬性次序的不同,所得到的決策樹也會不同。如何得到一棵決策樹既對訓(xùn)練數(shù)據(jù)有較好的擬合,又對未知數(shù)據(jù)有很好的預(yù)測呢?
首先,我們要解決兩個問題:
如何選擇較優(yōu)的特征屬性進(jìn)行分裂?每一次特征屬性的分裂,相當(dāng)于對訓(xùn)練數(shù)據(jù)集進(jìn)行再劃分,對應(yīng)于一次決策樹的生長。ID3算法定義了目標(biāo)函數(shù)來進(jìn)行特征選擇。
什么時候應(yīng)該停止分裂?有兩種自然情況應(yīng)該停止分裂,一是該節(jié)點對應(yīng)的所有樣本記錄均屬于同一類別,二是該節(jié)點對應(yīng)的所有樣本的特征屬性值均相等。但除此之外,是不是還應(yīng)該其他情況停止分裂呢?
2、決策樹算法
特征選擇
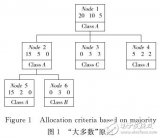
特征選擇指選擇最大化所定義目標(biāo)函數(shù)的特征。下面給出如下三種特征(Gender, Car Type, Customer ID)分裂的例子:
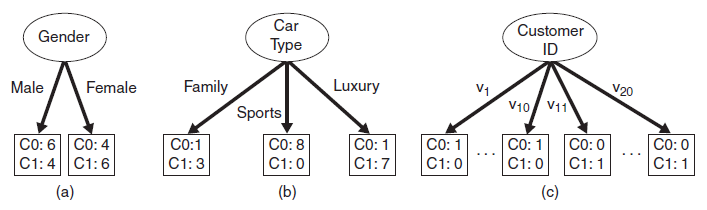
圖中有兩類類別(C0, C1),C0: 6是對C0類別的計數(shù)。直觀上,應(yīng)選擇Car Type特征進(jìn)行分裂,因為其類別的分布概率具有更大的傾斜程度,類別不確定程度更小。
為了衡量類別分布概率的傾斜程度,定義決策樹節(jié)點t的不純度(impurity),其滿足:不純度越小,則類別的分布概率越傾斜;下面給出不純度的的三種度量:
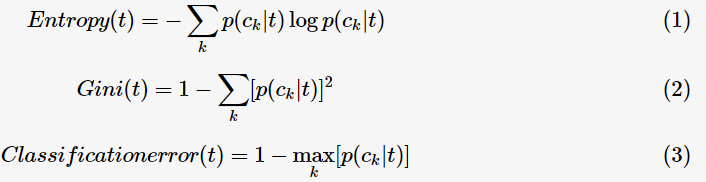
其中,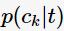 表示對于決策樹節(jié)點
表示對于決策樹節(jié)點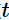
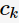 的概率。這三種不純度的度量是等價的,在等概率分布是達(dá)到最大值。
的概率。這三種不純度的度量是等價的,在等概率分布是達(dá)到最大值。
為了判斷分裂前后節(jié)點不純度的變化情況,目標(biāo)函數(shù)定義為信息增益(informationgain):
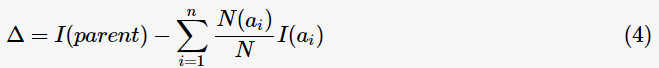
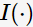
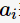 表示父節(jié)點分裂后的某子節(jié)點,
表示父節(jié)點分裂后的某子節(jié)點,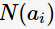 為其計數(shù),n為分裂后的子節(jié)點數(shù)。
為其計數(shù),n為分裂后的子節(jié)點數(shù)。
特別地,ID3算法選取熵值作為不純度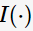 的度量,則
的度量,則
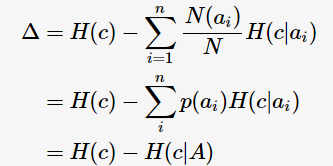
c指父節(jié)點對應(yīng)所有樣本記錄的類別; A表示選擇的特征屬性,即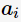 的集合。 那么,決策樹學(xué)習(xí)中的信息增益
的集合。 那么,決策樹學(xué)習(xí)中的信息增益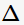 等價于訓(xùn)練數(shù)據(jù)集中類與特征的互信息,表示由于得知特征A的信息訓(xùn)練數(shù)據(jù)集c不確定性減少的程度。
等價于訓(xùn)練數(shù)據(jù)集中類與特征的互信息,表示由于得知特征A的信息訓(xùn)練數(shù)據(jù)集c不確定性減少的程度。
在特征分裂后,有些子節(jié)點的記錄數(shù)可能偏少,以至于影響分類結(jié)果。為了解決這個問題,CART算法提出了只進(jìn)行特征的二元分裂,即決策樹是一棵二叉樹;C4.5算法改進(jìn)分裂目標(biāo)函數(shù),用信息增益比(information gain ratio)來選擇特征:
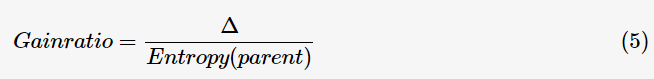
因而,特征選擇的過程等同于計算每個特征的信息增益,選擇最大信息增益的特征進(jìn)行分裂。此即回答前面所提出的第一個問題(選擇較優(yōu)特征)。ID3算法設(shè)定一閾值,當(dāng)最大信息增益小于閾值時,認(rèn)為沒有找到有較優(yōu)分類能力的特征,沒有往下繼續(xù)分裂的必要。根據(jù)最大表決原則,將最多計數(shù)的類別作為此葉子節(jié)點。即回答前面所提出的第二個問題(停止分裂條件)。
決策樹生成
ID3算法的核心是根據(jù)信息增益最大的準(zhǔn)則,遞歸地構(gòu)造決策樹;算法流程如下:
如果節(jié)點滿足停止分裂條件(所有記錄屬同一類別 or 最大信息增益小于閾值),將其置為葉子節(jié)點;
選擇信息增益最大的特征進(jìn)行分裂;
重復(fù)步驟1-2,直至分類完成。
C4.5算法流程與ID3相類似,只不過將信息增益改為信息增益比。
3、決策樹剪枝
過擬合
生成的決策樹對訓(xùn)練數(shù)據(jù)會有很好的分類效果,卻可能對未知數(shù)據(jù)的預(yù)測不準(zhǔn)確,即決策樹模型發(fā)生過擬合(overfitting)——訓(xùn)練誤差(training error)很小、泛化誤差(generalization error,亦可看作為test error)較大。下圖給出訓(xùn)練誤差、測試誤差(test error)隨決策樹節(jié)點數(shù)的變化情況:
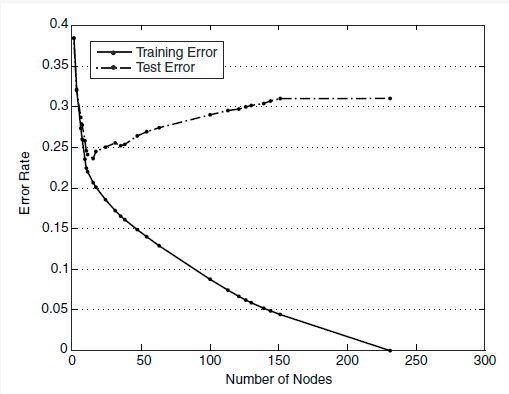
可以觀察到,當(dāng)節(jié)點數(shù)較小時,訓(xùn)練誤差與測試誤差均較大,即發(fā)生了欠擬合(underfitting)。當(dāng)節(jié)點數(shù)較大時,訓(xùn)練誤差較小,測試誤差卻很大,即發(fā)生了過擬合。只有當(dāng)節(jié)點數(shù)適中是,訓(xùn)練誤差居中,測試誤差較小;對訓(xùn)練數(shù)據(jù)有較好的擬合,同時對未知數(shù)據(jù)有很好的分類準(zhǔn)確率。
發(fā)生過擬合的根本原因是分類模型過于復(fù)雜,可能的原因如下:
訓(xùn)練數(shù)據(jù)集中有噪音樣本點,對訓(xùn)練數(shù)據(jù)擬合的同時也對噪音進(jìn)行擬合,從而影響了分類的效果;
決策樹的葉子節(jié)點中缺乏有分類價值的樣本記錄,也就是說此葉子節(jié)點應(yīng)被剪掉。
剪枝策略
為了解決過擬合,C4.5通過剪枝以減少模型的復(fù)雜度。[2]中提出一種簡單剪枝策略,通過極小化決策樹的整體損失函數(shù)(loss function)或代價函數(shù)(cost function)來實現(xiàn),決策樹T的損失函數(shù)為:
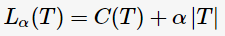
其中,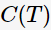 表示決策樹的訓(xùn)練誤差,
表示決策樹的訓(xùn)練誤差,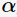 為調(diào)節(jié)參數(shù),
為調(diào)節(jié)參數(shù),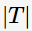 模型的復(fù)雜度。當(dāng)模型越復(fù)雜時,訓(xùn)練的誤差就越小。上述定義的損失正好做了兩者之間的權(quán)衡。
模型的復(fù)雜度。當(dāng)模型越復(fù)雜時,訓(xùn)練的誤差就越小。上述定義的損失正好做了兩者之間的權(quán)衡。
如果剪枝后損失函數(shù)減少了,即說明這是有效剪枝。具體剪枝算法可以由動態(tài)規(guī)劃等來實現(xiàn)。
-
數(shù)據(jù)挖掘
+關(guān)注
關(guān)注
1文章
406瀏覽量
24725 -
決策樹
+關(guān)注
關(guān)注
3文章
96瀏覽量
13833
原文標(biāo)題:【十大經(jīng)典數(shù)據(jù)挖掘算法】C4.5
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
機(jī)器學(xué)習(xí)中常用的決策樹算法技術(shù)解析
關(guān)于決策樹,這些知識點不可錯過
數(shù)據(jù)挖掘十大經(jīng)典算法,你都知道哪些!
一個基于粗集的決策樹規(guī)則提取算法
基于決策樹的數(shù)據(jù)挖掘算法應(yīng)用研究
改進(jìn)決策樹算法的應(yīng)用研究
使決策樹規(guī)模最小化算法
基于粗決策樹的動態(tài)規(guī)則提取算法
海量嘈雜數(shù)據(jù)決策樹算法
什么是決策樹?決策樹算法思考總結(jié)
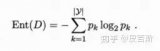
決策樹的構(gòu)成要素及算法
決策樹的基本概念/學(xué)習(xí)步驟/算法/優(yōu)缺點
什么是決策樹模型,決策樹模型的繪制方法



















評論