概述

卷積是一種線性運算,其本質是滑動平均思想,廣泛應用于圖像濾波。而隨著人工智能及深度學習的發展，卷積也在神經網絡中發揮重要的作用，如卷積神經網絡。本參考設計主要介紹如何基于INTEL 硬浮點的DSP Block實現32位單精度浮點的卷積運算，而針對定點及低精度的浮點運算，則需要對硬浮點DSP Block進行相應的替換即可。

原理分析

設:f(x), g(x)是兩個可積函數，作積分：

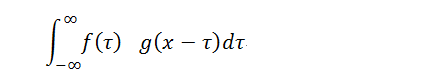
隨著x的不同取值，該積分定義了一個新的函數h(x)，稱為函數f(x)與g(x)的卷積，記為h(x)=f(x)*g(x)。

如果卷積的變量是序列x(n)和h(n)，則卷積的結果為

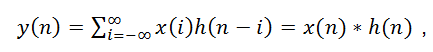
其中*表示卷積。因此兩個序列的卷積，實際上就是多項式的乘法，用個例子說明其工作原理。a = [7,5,4]; b = [6,7,9];則實現a和b的卷積，就是把a和b作為一個多項式的系數，按多項式的升冪或降冪排列，即為：

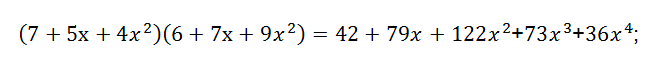
因此得到a*b=[42,79,122,73,36]；與Matlab運算結果一致。而二維卷積可以采用通用多項式乘積方法實現卷積運算。

基于INTEL FPGA的實現分析

如上我們確定了兩個序列的卷積等同于兩個多項式的乘法，因此當我們需要計算序列[a0,a1,a2, …,an-1]與[b0,b1,b2, …,bn-1]的卷積結果時，可以成立a,b兩個n階多項式，如下所示：

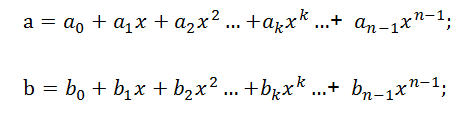
則[a0,a1,a2, …,an-1]與[b0,b1,b2, …,bn-1]的卷積結果即為由a*b得到的多項式的各項系數所組成的序列。令c=a*b，得到

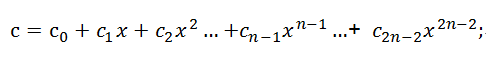
則由多項式c的各階系數所組成的新的序列[c0,c1,c2, …,c2n-1]即為[a0,a1,a2, …,an-1]與[b0,b1,b2, …,bn-1]的卷積結果。則按照高階多項式計算展開可得到：

┆┆

┆┆

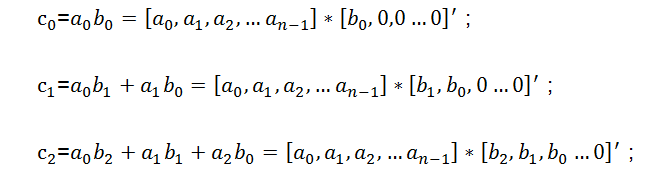
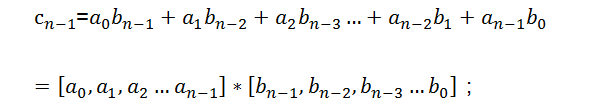
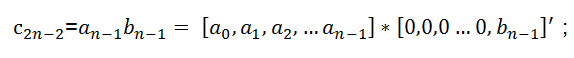
因此卷積的運算可以轉化為行向量與列向量相乘的結果，即乘累加的運算結構。

Intel FPGA在Arria10DSP Block中首次支持了單精度硬浮點DSP block,是行業內第一個支持單精度DSP block，硬浮點DSP block架構如圖1所示：

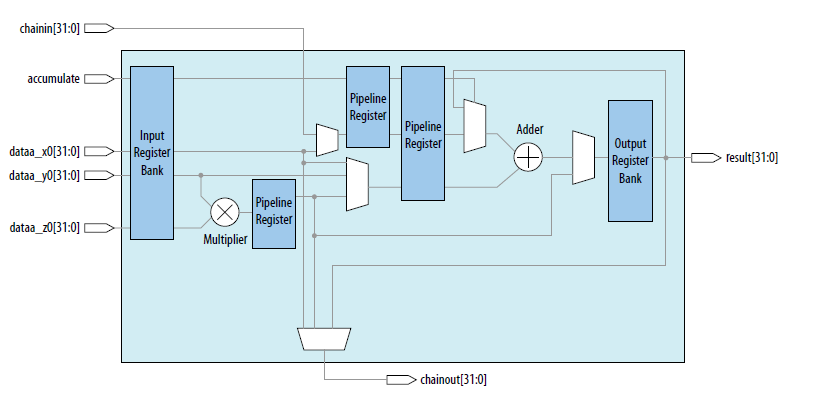
圖1 硬浮點DSPblock架構

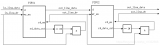
硬浮點DSP Block包含硬浮點乘法器，硬浮點加法器，支持乘累加運算，因此采用硬浮點DSPblock實現行列向量相乘是非常好的方式。下面我們針對一個實際的卷積運算，介紹如何基于INTEL硬浮點DSP block實現。假設我們需要求隨機數組a=[4,8,9,11]與b=[10,5,7,13]的卷積運算結果，則根據上面的分析，保持數組a順序不變，而數組b需根據上述分析結果，針對每一個卷積結果產生新的序列。所以整個實現包括數列重組模塊和硬浮點乘法器模塊及輸出處理。下面是實現框圖及仿真結果。

圖2 實現框圖

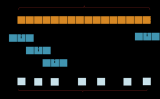
圖3 Modelsim仿真結果

仿真結果與Matlab實現結果一致，并且該設計中充分考慮了FPGA并行擴展特性，對于低速率要求的設計可采用DSP Block復用的方式節約DSP block數量。