1、引言
k-means與kNN雖然都是以k打頭,但卻是兩類算法——kNN為監(jiān)督學(xué)習(xí)中的分類算法,而k-means則是非監(jiān)督學(xué)習(xí)中的聚類算法;二者相同之處:均利用近鄰信息來標(biāo)注類別。
聚類是數(shù)據(jù)挖掘中一種非常重要的學(xué)習(xí)流派,指將未標(biāo)注的樣本數(shù)據(jù)中相似的分為同一類,正所謂“物以類聚,人以群分”嘛。k-means是聚類算法中最為簡單、高效的,核心思想:由用戶指定k個初始質(zhì)心(initial centroids),以作為聚類的類別(cluster),重復(fù)迭代直至算法收斂。
2、基本算法
在k-means算法中,用質(zhì)心來表示cluster;且容易證明k-means算法收斂等同于所有質(zhì)心不再發(fā)生變化。基本的k-means算法流程如下:
選取k個初始質(zhì)心(作為初始cluster); repeat: 對每個樣本點,計算得到距其最近的質(zhì)心,將其類別標(biāo)為該質(zhì)心所對應(yīng)的cluster; 重新計算k個cluser對應(yīng)的質(zhì)心; until 質(zhì)心不再發(fā)生變化
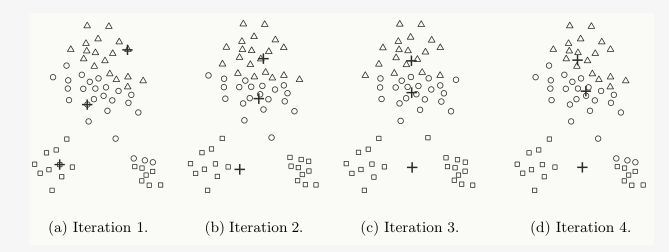
對于歐式空間的樣本數(shù)據(jù),以平方誤差和(sum of the squared error, SSE)作為聚類的目標(biāo)函數(shù),同時也可以衡量不同聚類結(jié)果好壞的指標(biāo):

表示樣本點 到cluster
到cluster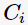 的質(zhì)心
的質(zhì)心 距離平方和;最優(yōu)的聚類結(jié)果應(yīng)使得SSE達到最小值。
距離平方和;最優(yōu)的聚類結(jié)果應(yīng)使得SSE達到最小值。
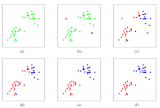
下圖中給出了一個通過4次迭代聚類3個cluster的例子:

k-means存在缺點:
k-means是局部最優(yōu)的,容易受到初始質(zhì)心的影響;比如在下圖中,因選擇初始質(zhì)心不恰當(dāng)而造成次優(yōu)的聚類結(jié)果(SSE較大):
同時,k值的選取也會直接影響聚類結(jié)果,最優(yōu)聚類的k值應(yīng)與樣本數(shù)據(jù)本身的結(jié)構(gòu)信息相吻合,而這種結(jié)構(gòu)信息是很難去掌握,因此選取最優(yōu)k值是非常困難的。
3、優(yōu)化
為了解決上述存在缺點,在基本k-means的基礎(chǔ)上發(fā)展而來二分 (bisecting) k-means,其主要思想:一個大cluster進行分裂后可以得到兩個小的cluster;為了得到k個cluster,可進行k-1次分裂。算法流程如下:
初始只有一個cluster包含所有樣本點; repeat: 從待分裂的clusters中選擇一個進行二元分裂,所選的cluster應(yīng)使得SSE最小; until 有k個cluster
上述算法流程中,為從待分裂的clusters中求得局部最優(yōu)解,可以采取暴力方法:依次對每個待分裂的cluster進行二元分裂(bisect)以求得最優(yōu)分裂。二分k-means算法聚類過程如圖:

從圖中,我們觀察到:二分k-means算法對初始質(zhì)心的選擇不太敏感,因為初始時只選擇一個質(zhì)心。
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4327瀏覽量
62573 -
聚類算法
+關(guān)注
關(guān)注
2文章
118瀏覽量
12126 -
K-means
+關(guān)注
關(guān)注
0文章
28瀏覽量
11293
原文標(biāo)題:【十大經(jīng)典數(shù)據(jù)挖掘算法】k-means
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
改進的k-means聚類算法在供電企業(yè)CRM中的應(yīng)用
Web文檔聚類中k-means算法的改進
K-means+聚類算法研究綜述

基于密度的K-means算法在聚類數(shù)目中應(yīng)用
K-Means算法改進及優(yōu)化
基于布谷鳥搜索的K-means聚類算法
熵加權(quán)多視角核K-means算法
k-means算法原理解析




 基本的k-means算法流程
基本的k-means算法流程










評論