很多機器學(xué)習(xí)的問題都會涉及到有著幾千甚至數(shù)百萬維的特征的訓(xùn)練實例。這不僅讓訓(xùn)練過程變得非常緩慢,同時還很難找到一個很好的解,我們接下來就會遇到這種情況。這種問題通常被稱為維數(shù)災(zāi)難(curse of dimentionality)。
幸運的是,在現(xiàn)實生活中我們經(jīng)常可以極大的降低特征維度,將一個十分棘手的問題轉(zhuǎn)變成一個可以較為容易解決的問題。例如,對于 MNIST 圖片集(第 3 章中提到):圖片四周邊緣部分的像素幾乎總是白的,因此你完全可以將這些像素從你的訓(xùn)練集中扔掉而不會丟失太多信息。圖 7-6 向我們證實了這些像素的確對我們的分類任務(wù)是完全不重要的。同時,兩個相鄰的像素往往是高度相關(guān)的:如果你想要將他們合并成一個像素(比如取這兩個像素點的平均值)你并不會丟失很多信息。
警告:降維肯定會丟失一些信息(這就好比將一個圖片壓縮成 JPEG 的格式會降低圖像的質(zhì)量),因此即使這種方法可以加快訓(xùn)練的速度,同時也會讓你的系統(tǒng)表現(xiàn)的稍微差一點。降維會讓你的工作流水線更復(fù)雜因而更難維護。所有你應(yīng)該先嘗試使用原始的數(shù)據(jù)來訓(xùn)練,如果訓(xùn)練速度太慢的話再考慮使用降維。在某些情況下,降低訓(xùn)練集數(shù)據(jù)的維度可能會篩選掉一些噪音和不必要的細(xì)節(jié),這可能會讓你的結(jié)果比降維之前更好(這種情況通常不會發(fā)生;它只會加快你訓(xùn)練的速度)。
降維除了可以加快訓(xùn)練速度外,在數(shù)據(jù)可視化方面(或者 DataViz)也十分有用。降低特征維度到 2(或者 3)維從而可以在圖中畫出一個高維度的訓(xùn)練集,讓我們可以通過視覺直觀的發(fā)現(xiàn)一些非常重要的信息,比如聚類。
在這一章里,我們將會討論維數(shù)災(zāi)難問題并且了解在高維空間的數(shù)據(jù)。然后,我們將會展示兩種主要的降維方法:投影(projection)和流形學(xué)習(xí)(Manifold Learning),同時我們還會介紹三種流行的降維技術(shù):主成分分析(PCA),核主成分分析(Kernel PCA)和局部線性嵌入(LLE)。
維數(shù)災(zāi)難
我們已經(jīng)習(xí)慣生活在一個三維的世界里,以至于當(dāng)我們嘗試想象更高維的空間時,我們的直覺不管用了。即使是一個基本的 4D 超正方體也很難在我們的腦中想象出來(見圖 8-1),更不用說一個 200 維的橢球彎曲在一個 1000 維的空間里了。
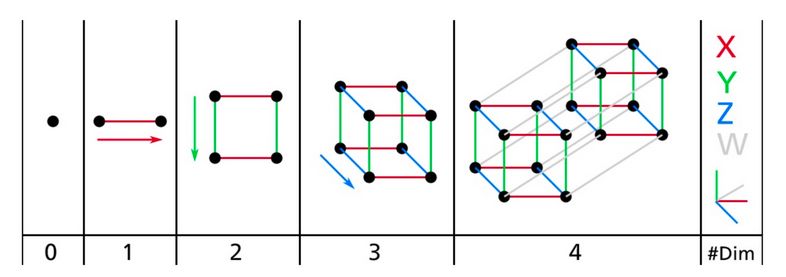
圖 8-1 點,線,方形,立方體和超正方體(0D 到 4D 超正方體)
這表明很多物體在高維空間表現(xiàn)的十分不同。比如,如果你在一個正方形單元中隨機取一個點(一個1×1的正方形),那么隨機選的點離所有邊界大于 0.001(靠近中間位置)的概率為 0.4%(1 - 0.998^2)(換句話說,一個隨機產(chǎn)生的點不大可能嚴(yán)格落在某一個維度上。但是在一個 1,0000 維的單位超正方體(一個1×1×...×1的立方體,有 10,000 個 1),這種可能性超過了 99.999999%。在高維超正方體中,大多數(shù)點都分布在邊界處。
還有一個更麻煩的區(qū)別:如果你在一個平方單位中隨機選取兩個點,那么這兩個點之間的距離平均約為 0.52。如果您在單位 3D 立方體中選取兩個隨機點,平均距離將大致為 0.66。但是,在一個 1,000,000 維超立方體中隨機抽取兩點呢?那么,平均距離,信不信由你,大概為 408.25(大致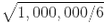 )!這非常違反直覺:當(dāng)它們都位于同一單元超立方體內(nèi)時,兩點是怎么距離這么遠(yuǎn)的?這一事實意味著高維數(shù)據(jù)集有很大風(fēng)險分布的非常稀疏:大多數(shù)訓(xùn)練實例可能彼此遠(yuǎn)離。當(dāng)然,這也意味著一個新實例可能遠(yuǎn)離任何訓(xùn)練實例,這使得預(yù)測的可靠性遠(yuǎn)低于我們處理較低維度數(shù)據(jù)的預(yù)測,因為它們將基于更大的推測(extrapolations)。簡而言之,訓(xùn)練集的維度越高,過擬合的風(fēng)險就越大。
)!這非常違反直覺:當(dāng)它們都位于同一單元超立方體內(nèi)時,兩點是怎么距離這么遠(yuǎn)的?這一事實意味著高維數(shù)據(jù)集有很大風(fēng)險分布的非常稀疏:大多數(shù)訓(xùn)練實例可能彼此遠(yuǎn)離。當(dāng)然,這也意味著一個新實例可能遠(yuǎn)離任何訓(xùn)練實例,這使得預(yù)測的可靠性遠(yuǎn)低于我們處理較低維度數(shù)據(jù)的預(yù)測,因為它們將基于更大的推測(extrapolations)。簡而言之,訓(xùn)練集的維度越高,過擬合的風(fēng)險就越大。
理論上來說,維數(shù)爆炸的一個解決方案是增加訓(xùn)練集的大小從而達(dá)到擁有足夠密度的訓(xùn)練集。不幸的是,在實踐中,達(dá)到給定密度所需的訓(xùn)練實例的數(shù)量隨著維度的數(shù)量呈指數(shù)增長。如果只有 100 個特征(比 MNIST 問題要少得多)并且假設(shè)它們均勻分布在所有維度上,那么如果想要各個臨近的訓(xùn)練實例之間的距離在 0.1 以內(nèi),您需要比宇宙中的原子還要多的訓(xùn)練實例。
降維的主要方法
在我們深入研究具體的降維算法之前,我們來看看降低維度的兩種主要方法:投影和流形學(xué)習(xí)。
投影(Projection)
在大多數(shù)現(xiàn)實生活的問題中,訓(xùn)練實例并不是在所有維度上均勻分布的。許多特征幾乎是常數(shù),而其他特征則高度相關(guān)(如前面討論的 MNIST)。結(jié)果,所有訓(xùn)練實例實際上位于(或接近)高維空間的低維子空間內(nèi)。這聽起來有些抽象,所以我們不妨來看一個例子。在圖 8-2 中,您可以看到由圓圈表示的 3D 數(shù)據(jù)集。
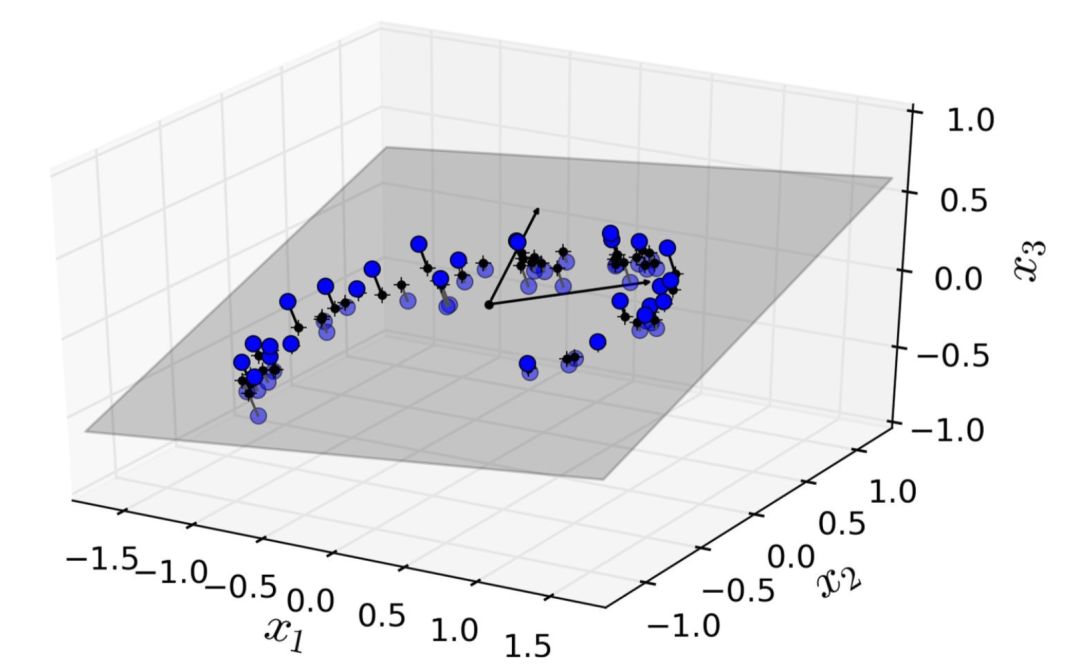
圖 8-2 一個分布接近于2D子空間的3D數(shù)據(jù)集
注意到所有訓(xùn)練實例的分布都貼近一個平面:這是高維(3D)空間的較低維(2D)子空間。現(xiàn)在,如果我們將每個訓(xùn)練實例垂直投影到這個子空間上(就像將短線連接到平面的點所表示的那樣),我們就可以得到如圖8-3所示的新2D數(shù)據(jù)集。鐺鐺鐺!我們剛剛將數(shù)據(jù)集的維度從 3D 降低到了 2D。請注意,坐標(biāo)軸對應(yīng)于新的特征z1和z2(平面上投影的坐標(biāo))。
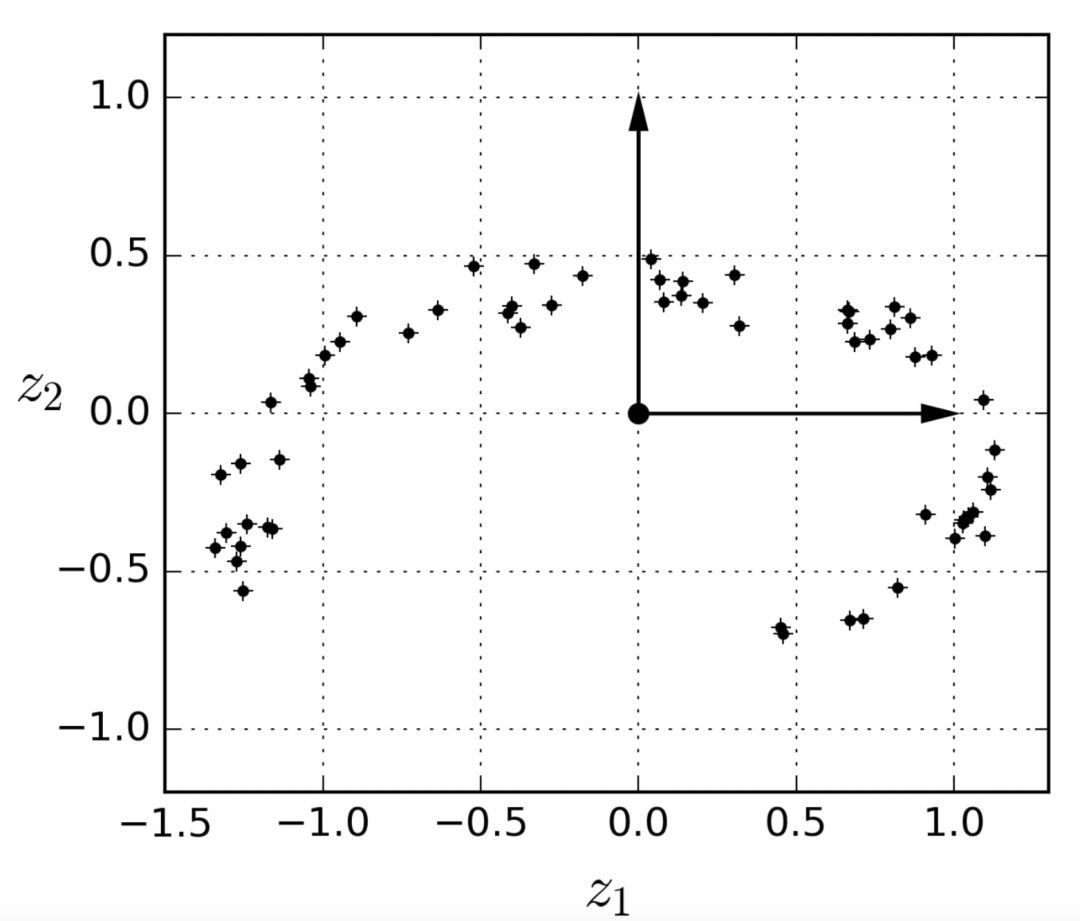
圖 8-3 一個經(jīng)過投影后的新的 2D 數(shù)據(jù)集
但是,投影并不總是降維的最佳方法。在很多情況下,子空間可能會扭曲和轉(zhuǎn)動,比如圖 8-4 所示的著名瑞士滾動玩具數(shù)據(jù)集。
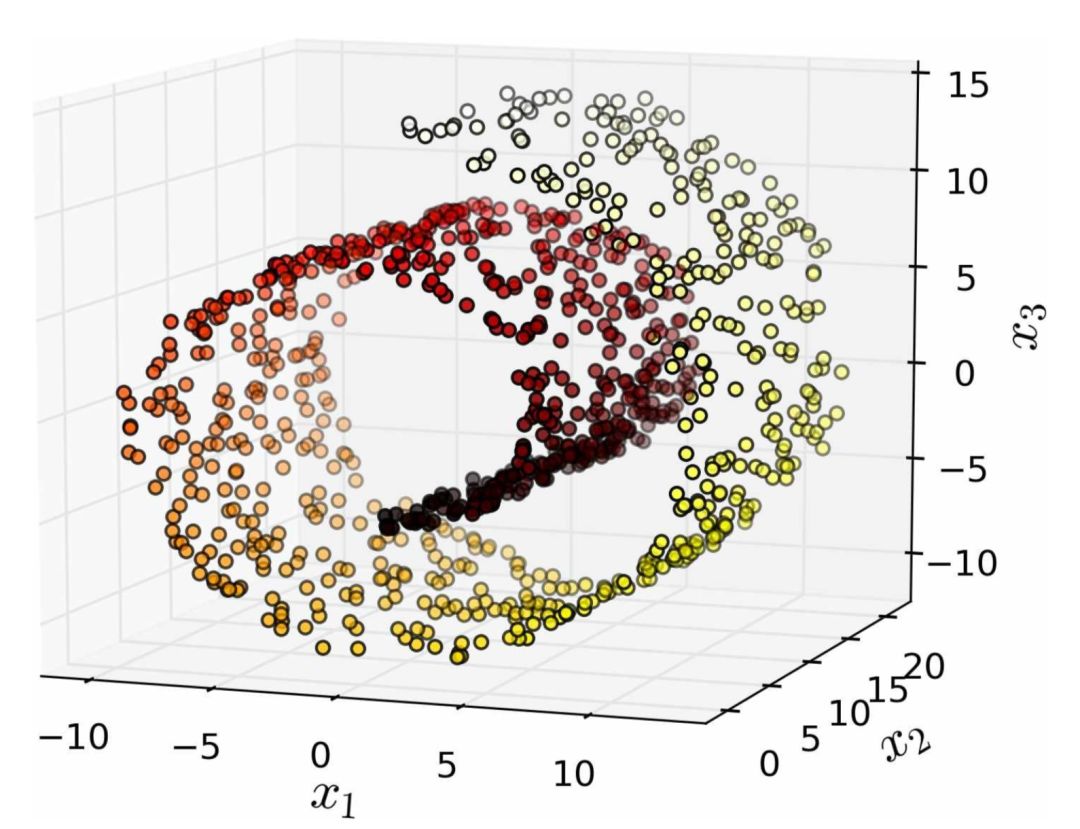
圖 8-4 瑞士滾動數(shù)玩具數(shù)據(jù)集
簡單地將數(shù)據(jù)集投射到一個平面上(例如,直接丟棄x3)會將瑞士卷的不同層疊在一起,如圖 8-5 左側(cè)所示。但是,你真正想要的是展開瑞士卷所獲取到的類似圖 8-5 右側(cè)的 2D 數(shù)據(jù)集。
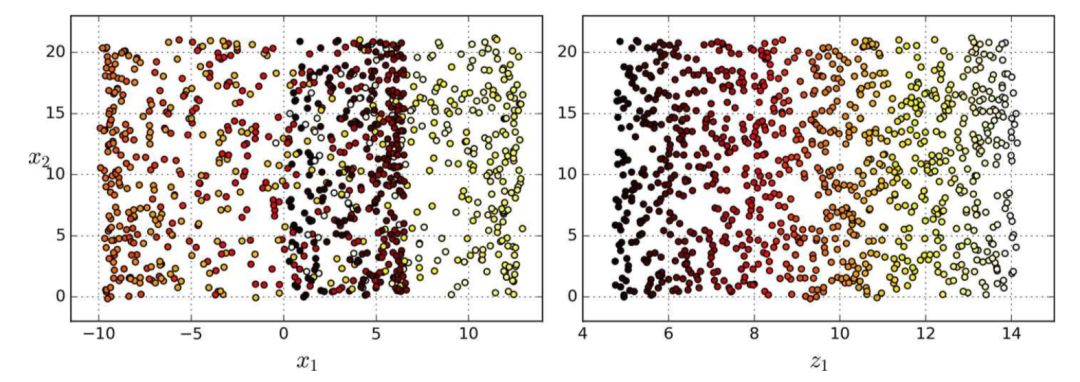
圖 8-5 投射到平面的壓縮(左)vs 展開瑞士卷(右)
流形學(xué)習(xí)
瑞士卷一個是二維流形的例子。簡而言之,二維流形是一種二維形狀,它可以在更高維空間中彎曲或扭曲。更一般地,一個d維流形是類似于d維超平面的n維空間(其中d < n)的一部分。在我們?nèi)鹗烤磉@個例子中,d = 2,n = 3:它有些像 2D 平面,但是它實際上是在第三維中卷曲。
許多降維算法通過對訓(xùn)練實例所在的流形進(jìn)行建模從而達(dá)到降維目的;這叫做流形學(xué)習(xí)。它依賴于流形猜想(manifold assumption),也被稱為流形假設(shè)(manifold hypothesis),它認(rèn)為大多數(shù)現(xiàn)實世界的高維數(shù)據(jù)集大都靠近一個更低維的流形。這種假設(shè)經(jīng)常在實踐中被證實。
讓我們再回到 MNIST 數(shù)據(jù)集:所有手寫數(shù)字圖像都有一些相似之處。它們由連線組成,邊界是白色的,大多是在圖片中中間的,等等。如果你隨機生成圖像,只有一小部分看起來像手寫數(shù)字。換句話說,如果您嘗試創(chuàng)建數(shù)字圖像,那么您的自由度遠(yuǎn)低于您生成任何隨便一個圖像時的自由度。這些約束往往會將數(shù)據(jù)集壓縮到較低維流形中。
流形假設(shè)通常包含著另一個隱含的假設(shè):你現(xiàn)在的手上的工作(例如分類或回歸)如果在流形的較低維空間中表示,那么它們會變得更簡單。例如,在圖 8-6 的第一行中,瑞士卷被分為兩類:在三維空間中(圖左上),分類邊界會相當(dāng)復(fù)雜,但在二維展開的流形空間中(圖右上),分類邊界是一條簡單的直線。
但是,這個假設(shè)并不總是成立。例如,在圖 8-6 的最下面一行,決策邊界位于x1 = 5(圖左下)。這個決策邊界在原始三維空間(一個垂直平面)看起來非常簡單,但在展開的流形中卻變得更復(fù)雜了(四個獨立線段的集合)(圖右下)。
簡而言之,如果在訓(xùn)練模型之前降低訓(xùn)練集的維數(shù),那訓(xùn)練速度肯定會加快,但并不總是會得出更好的訓(xùn)練效果;這一切都取決于數(shù)據(jù)集。
希望你現(xiàn)在對于維數(shù)爆炸以及降維算法如何解決這個問題有了一定的理解,特別是對流形假設(shè)提出的內(nèi)容。本章的其余部分將介紹一些最流行的降維算法。
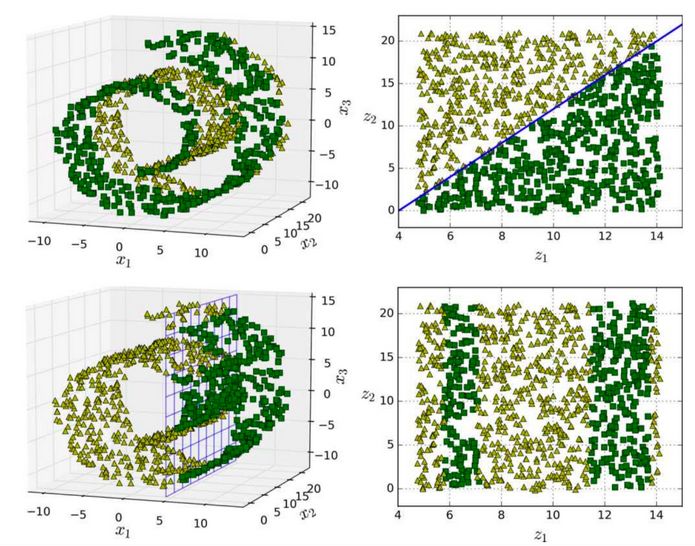
圖 8-6 決策邊界并不總是會在低維空間中變的簡單
-
3D
+關(guān)注
關(guān)注
9文章
2951瀏覽量
109443 -
降維
+關(guān)注
關(guān)注
0文章
10瀏覽量
7706 -
數(shù)據(jù)集
+關(guān)注
關(guān)注
4文章
1222瀏覽量
25275
原文標(biāo)題:【翻譯】Sklearn 與 TensorFlow 機器學(xué)習(xí)實用指南 —— 第8章 降維(上)
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
基于多傳感器數(shù)據(jù)融合處理實現(xiàn)與城市三維空間和時間配準(zhǔn)


labview 利用三維空間畫了一個球,然后想在球面上畫幾個點
基于麥克風(fēng)陣列模擬人耳進(jìn)行三維空間的聲源定位
基于單元區(qū)域的高維數(shù)據(jù)聚類算法
基于交流伺服控制的三維空間磁場與磁力測試技術(shù)
基于Autoencoder網(wǎng)絡(luò)的數(shù)據(jù)降維和重構(gòu)
基于伺服控制的三維空間磁場與磁力測試系統(tǒng)
高維數(shù)據(jù)相似性連接查詢算法
什么是高維數(shù)據(jù)_高維數(shù)據(jù)如何定義

高維空間逼近最近鄰評測



















評論