按照我做項目的經(jīng)驗，來了項目，首先是分析項目的目的和需求，了解這個項目屬于什么問題，要達(dá)到什么效果。然后提取數(shù)據(jù)，做基本的數(shù)據(jù)清洗。第三步是特征工程，這個屬于臟活累活，需要耗費很大的精力，如果特征工程做的好，那么，后面選擇什么算法其實差異不大，反之，不管選擇什么算法，效果都不會有突破性的提高。第四步，是跑算法，通常情況下，我會把所有能跑的算法先跑一遍，看看效果，分析一下precesion/recall和f1-score，看看有沒有什么異常（譬如有好幾個算法precision特別好，但是recall特別低，這就要從數(shù)據(jù)中找原因，或者從算法中看是不是因為算法不適合這個數(shù)據(jù)），如果沒有異常，那么就進(jìn)行下一步，選擇一兩個跑的結(jié)果最好的算法進(jìn)行調(diào)優(yōu)。調(diào)優(yōu)的方法很多，調(diào)整參數(shù)的話可以用網(wǎng)格搜索、隨機搜索等，調(diào)整性能的話，可以根據(jù)具體的數(shù)據(jù)和場景進(jìn)行具體分析。調(diào)優(yōu)后再跑一邊算法，看結(jié)果有沒有提高，如果沒有，找原因，數(shù)據(jù) or 算法？是數(shù)據(jù)質(zhì)量不好，還是特征問題還是算法問題。一個一個排查，找解決方法。

特征問題就回到第三步再進(jìn)行特征工程，數(shù)據(jù)質(zhì)量問題就回到第一步看數(shù)據(jù)清洗有沒有遺漏，異常值是否影響了算法的結(jié)果，算法問題就回到第四步，看算法流程中哪一步出了問題。如果實在不行，可以搜一下相關(guān)的論文，看看論文中有沒有解決方法。這樣反復(fù)來幾遍，就可以出結(jié)果了，寫技術(shù)文檔和分析報告，再向業(yè)務(wù)人員或產(chǎn)品講解我們做的東西，然后他們再提建議/該需求，不斷循環(huán)，最后代碼上線，改bug，直到結(jié)項。

直觀來看，可以用一個流程圖來表示：

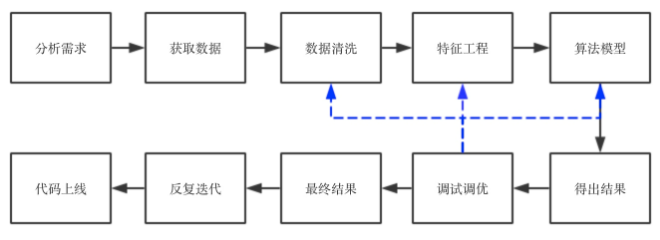
今天講數(shù)據(jù)清洗，為什么要進(jìn)行數(shù)據(jù)清洗呢？我們在書上看到的數(shù)據(jù)，譬如常見的iris數(shù)據(jù)集，房價數(shù)據(jù)，電影評分?jǐn)?shù)據(jù)集等等，數(shù)據(jù)質(zhì)量都很高，沒有缺失值，沒有異常點，也沒有噪音，而在真實數(shù)據(jù)中，我們拿到的數(shù)據(jù)可能包含了大量的缺失值，可能包含大量的噪音，也可能因為人工錄入錯誤導(dǎo)致有異常點存在，對我們挖據(jù)出有效信息造成了一定的困擾，所以我們需要通過一些方法，盡量提高數(shù)據(jù)的質(zhì)量。數(shù)據(jù)清洗一般包括以下幾個步驟：

一.分析數(shù)據(jù)

二.缺失值處理

三.異常值處理

四.去重處理

五.噪音數(shù)據(jù)處理

六.一些實用的數(shù)據(jù)處理小工具

一.分析數(shù)據(jù)

在實際項目中，當(dāng)我們確定需求后就會去找相應(yīng)的數(shù)據(jù)，拿到數(shù)據(jù)后，首先要對數(shù)據(jù)進(jìn)行描述性統(tǒng)計分析，查看哪些數(shù)據(jù)是不合理的，也可以知道數(shù)據(jù)的基本情況。如果是銷售額數(shù)據(jù)可以通過分析不同商品的銷售總額、人均消費額、人均消費次數(shù)等，同一商品的不同時間的消費額、消費頻次等等，了解數(shù)據(jù)的基本情況。此外可以通過作圖的方式了解數(shù)據(jù)的質(zhì)量，有無異常點，有無噪音等。舉個例子（這里數(shù)據(jù)較少，就直接用R作圖了）：

#一組年薪超過10萬元的經(jīng)理收入 pay=c(11,19,14,22,14,28,13,81,12,43,11,16,31,16,23.42,22,26,17,22,13,27,180,16,43,82,14,11,51,76,28,66,29,14,14,65,37,16,37,35,39,27,14,17,13,38,28,40,85,32,25,26,16,12,54,40,18,27,16,14,33,29,77,50,19,34) par(mfrow=c(2,2))#將繪圖窗口改成2*2，可同時顯示四幅圖 hist(pay)#繪制直方圖 dotchart(pay)#繪制點圖 barplot(pay,horizontal=T)#繪制箱型圖 qqnorm(pay);qqline(pay)#繪制Q-Q圖

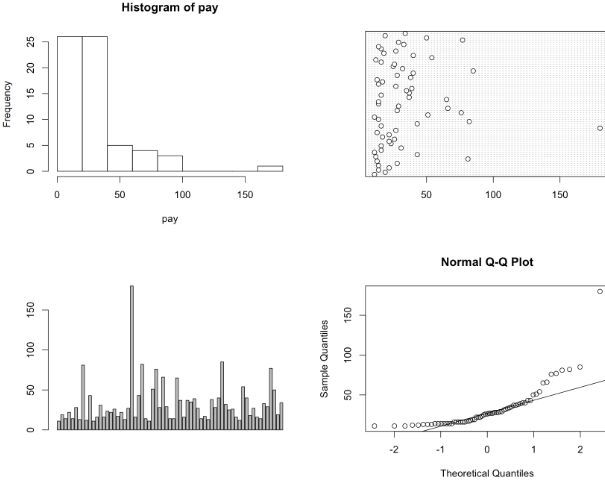
上面四幅圖可以很清楚的看出，180是異常值，即第23個數(shù)據(jù)需要清理。

python中也包含了大量的統(tǒng)計命令，其中主要的統(tǒng)計特征函數(shù)如下圖所示：

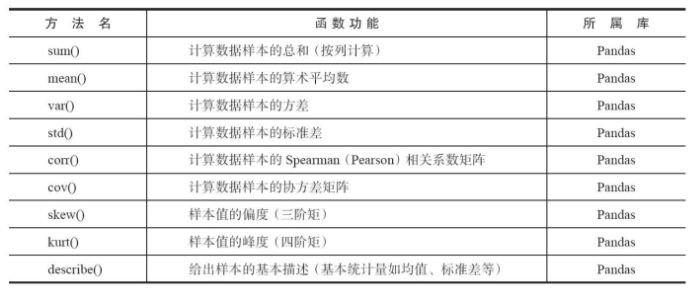
二.缺失值處理

缺失值在實際數(shù)據(jù)中是不可避免的問題，有的人看到有缺失的數(shù)據(jù)就直接刪除了，有的人直接賦予0值或者某一個特殊的值，那么到底該怎么處理呢？對于不同的數(shù)據(jù)場景應(yīng)該采取不同的策略，首先應(yīng)該判斷缺失值的分布情況：

1 import scipy as sp 2 data = sp.genfromtxt("web_traffic.tsv",delimiter = "\t")

數(shù)據(jù)情況如下：

>>>data array([[ 1.00000000e+00, 2.27200000e+03], [ 2.00000000e+00, nan], [ 3.00000000e+00, 1.38600000e+03], ..., [ 7.41000000e+02, 5.39200000e+03], [ 7.42000000e+02, 5.90600000e+03], [ 7.43000000e+02, 4.88100000e+03]]) >>> print data[:10] [[ 1.00000000e+00 2.27200000e+03] [ 2.00000000e+00 nan] [ 3.00000000e+00 1.38600000e+03] [ 4.00000000e+00 1.36500000e+03] [ 5.00000000e+00 1.48800000e+03] [ 6.00000000e+00 1.33700000e+03] [ 7.00000000e+00 1.88300000e+03] [ 8.00000000e+00 2.28300000e+03] [ 9.00000000e+00 1.33500000e+03] [ 1.00000000e+01 1.02500000e+03]] >>> data.shape (743, 2)

可以看到，第2列已經(jīng)出現(xiàn)了缺失值，現(xiàn)在我們來看一下缺失值的數(shù)量：

1 >>> x = data[:,0] 2 >>> y = data[:,1] 3 >>> sp.sum(sp.isnan(y)) 4 8

在743個數(shù)據(jù)里只有8個數(shù)據(jù)缺失，所以刪除它們對于整體數(shù)據(jù)情況影響不大。當(dāng)然，這是缺失值少的情況下，在缺失值值比較多，而這個維度的信息還很重要的時候（因為缺失值如果占了95%以上，可以直接去掉這個維度的數(shù)據(jù)了），直接刪除會對后面的算法跑的結(jié)果造成不好的影響。我們常用的方法有以下幾種：

1.直接刪除----適合缺失值數(shù)量較小，并且是隨機出現(xiàn)的，刪除它們對整體數(shù)據(jù)影響不大的情況。

2.使用一個全局常量填充---譬如將缺失值用“Unknown”等填充，但是效果不一定好，因為算法可能會把它識別為一個新的類別，一般很少用。

3.使用均值或中位數(shù)代替----優(yōu)點：不會減少樣本信息，處理簡單。缺點：當(dāng)缺失數(shù)據(jù)不是隨機數(shù)據(jù)時會產(chǎn)生偏差.對于正常分布的數(shù)據(jù)可以使用均值代替，如果數(shù)據(jù)是傾斜的，使用中位數(shù)可能更好。

4.插補法

1）隨機插補法----從總體中隨機抽取某個樣本代替缺失樣本

2）多重插補法----通過變量之間的關(guān)系對缺失數(shù)據(jù)進(jìn)行預(yù)測，利用蒙特卡洛方法生成多個完整的數(shù)據(jù)集，在對這些數(shù)據(jù)集進(jìn)行分析，最后對分析結(jié)果進(jìn)行匯總處理

3）熱平臺插補----指在非缺失數(shù)據(jù)集中找到一個與缺失值所在樣本相似的樣本（匹配樣本），利用其中的觀測值對缺失值進(jìn)行插補。

優(yōu)點：簡單易行，準(zhǔn)去率較高

缺點：變量數(shù)量較多時，通常很難找到與需要插補樣本完全相同的樣本。但我們可以按照某些變量將數(shù)據(jù)分層，在層中對缺失值實用均值插補

4)拉格朗日差值法和牛頓插值法（簡單高效，數(shù)值分析里的內(nèi)容，數(shù)學(xué)公式以后再補 = =）

5.建模法

可以用回歸、使用貝葉斯形式化方法的基于推理的工具或決策樹歸納確定。例如，利用數(shù)據(jù)集中其他數(shù)據(jù)的屬性，可以構(gòu)造一棵判定樹，來預(yù)測缺失值的值。

以上方法各有優(yōu)缺點，具體情況要根據(jù)實際數(shù)據(jù)分分布情況、傾斜程度、缺失值所占比例等等來選擇方法。一般而言，建模法是比較常用的方法，它根據(jù)已有的值來預(yù)測缺失值，準(zhǔn)確率更高。

三.異常值處理

異常值我們通常也稱為“離群點”。在講分析數(shù)據(jù)時，我們舉了個例子說明如何發(fā)現(xiàn)離群點，除了畫圖（畫圖其實并不常用，因為數(shù)據(jù)量多時不好畫圖，而且慢），還有很多其他方法:

1.簡單的統(tǒng)計分析

拿到數(shù)據(jù)后可以對數(shù)據(jù)進(jìn)行一個簡單的描述性統(tǒng)計分析，譬如最大最小值可以用來判斷這個變量的取值是否超過了合理的范圍，如客戶的年齡為-20歲或200歲，顯然是不合常理的，為異常值。

在python中可以直接用pandas的describe()：

>>> import pandas as pd >>> data = pd.read_table("web_traffic.tsv",header = None) >>> data.describe() 0 1 count 743.000000 735.000000 mean 372.000000 1962.165986 std 214.629914 860.720997 min 1.000000 472.000000 25% 186.500000 1391.000000 50% 372.000000 1764.000000 75% 557.500000 2217.500000 max 743.000000 5906.000000

2.3?原則

如果數(shù)據(jù)服從正態(tài)分布，在3?原則下，異常值為一組測定值中與平均值的偏差超過3倍標(biāo)準(zhǔn)差的值。如果數(shù)據(jù)服從正態(tài)分布，距離平均值3?之外的值出現(xiàn)的概率為P(|x-u| > 3?) <= 0.003，屬于極個別的小概率事件。如果數(shù)據(jù)不服從正態(tài)分布，也可以用遠(yuǎn)離平均值的多少倍標(biāo)準(zhǔn)差來描述。

3.箱型圖分析

箱型圖提供了識別異常值的一個標(biāo)準(zhǔn)：如果一個值小于QL01.5IQR或大于OU-1.5IQR的值，則被稱為異常值。QL為下四分位數(shù)，表示全部觀察值中有四分之一的數(shù)據(jù)取值比它小；QU為上四分位數(shù)，表示全部觀察值中有四分之一的數(shù)據(jù)取值比它大；IQR為四分位數(shù)間距，是上四分位數(shù)QU與下四分位數(shù)QL的差值，包含了全部觀察值的一半。箱型圖判斷異常值的方法以四分位數(shù)和四分位距為基礎(chǔ)，四分位數(shù)具有魯棒性：25%的數(shù)據(jù)可以變得任意遠(yuǎn)并且不會干擾四分位數(shù)，所以異常值不能對這個標(biāo)準(zhǔn)施加影響。因此箱型圖識別異常值比較客觀，在識別異常值時有一定的優(yōu)越性。

4.基于模型檢測

首先建立一個數(shù)據(jù)模型，異常是那些同模型不能完美擬合的對象；如果模型是簇的集合，則異常是不顯著屬于任何簇的對象；在使用回歸模型時，異常是相對遠(yuǎn)離預(yù)測值的對象

優(yōu)缺點：1.有堅實的統(tǒng)計學(xué)理論基礎(chǔ)，當(dāng)存在充分的數(shù)據(jù)和所用的檢驗類型的知識時，這些檢驗可能非常有效；2.對于多元數(shù)據(jù)，可用的選擇少一些，并且對于高維數(shù)據(jù)，這些檢測可能性很差。

5.基于距離

通常可以在對象之間定義鄰近性度量，異常對象是那些遠(yuǎn)離其他對象的對象

優(yōu)缺點：1.簡單；2.缺點：基于鄰近度的方法需要O(m2)時間，大數(shù)據(jù)集不適用；3.該方法對參數(shù)的選擇也是敏感的；4.不能處理具有不同密度區(qū)域的數(shù)據(jù)集，因為它使用全局閾值，不能考慮這種密度的變化。

6.基于密度

當(dāng)一個點的局部密度顯著低于它的大部分近鄰時才將其分類為離群點。適合非均勻分布的數(shù)據(jù)。

優(yōu)缺點：1.給出了對象是離群點的定量度量，并且即使數(shù)據(jù)具有不同的區(qū)域也能夠很好的處理；2.與基于距離的方法一樣，這些方法必然具有O(m2)的時間復(fù)雜度。對于低維數(shù)據(jù)使用特定的數(shù)據(jù)結(jié)構(gòu)可以達(dá)到O(mlogm)；3.參數(shù)選擇困難。雖然算法通過觀察不同的k值，取得最大離群點得分來處理該問題，但是，仍然需要選擇這些值的上下界。

7.基于聚類：

基于聚類的離群點：一個對象是基于聚類的離群點，如果該對象不強屬于任何簇。離群點對初始聚類的影響：如果通過聚類檢測離群點，則由于離群點影響聚類，存在一個問題：結(jié)構(gòu)是否有效。為了處理該問題，可以使用如下方法：對象聚類，刪除離群點，對象再次聚類（這個不能保證產(chǎn)生最優(yōu)結(jié)果）。

優(yōu)缺點：1.基于線性和接近線性復(fù)雜度（k均值）的聚類技術(shù)來發(fā)現(xiàn)離群點可能是高度有效的；2.簇的定義通常是離群點的補，因此可能同時發(fā)現(xiàn)簇和離群點；3.產(chǎn)生的離群點集和它們的得分可能非常依賴所用的簇的個數(shù)和數(shù)據(jù)中離群點的存在性；4.聚類算法產(chǎn)生的簇的質(zhì)量對該算法產(chǎn)生的離群點的質(zhì)量影響非常大。

處理方法：

1.刪除異常值----明顯看出是異常且數(shù)量較少可以直接刪除

2.不處理---如果算法對異常值不敏感則可以不處理，但如果算法對異常值敏感，則最好不要用，如基于距離計算的一些算法，包括kmeans，knn之類的。

3.平均值替代----損失信息小，簡單高效。

4.視為缺失值----可以按照處理缺失值的方法來處理

四.去重處理

以DataFrame數(shù)據(jù)格式為例：

#創(chuàng)建數(shù)據(jù)，data里包含重復(fù)數(shù)據(jù) >>> data = pd.DataFrame({'v1':['a']*5+['b']* 4,'v2':[1,2,2,2,3,4,4,5,3]}) >>> data v1 v2 0 a 1 1 a 2 2 a 2 3 a 2 4 a 3 5 b 4 6 b 4 7 b 5 8 b 3 #DataFrame的duplicated方法返回一個布爾型Series，表示各行是否是重復(fù)行 >>> data.duplicated() 0 False 1 False 2 True 3 True 4 False 5 False 6 True 7 False 8 False dtype: bool #drop_duplicates方法用于返回一個移除了重復(fù)行的DataFrame >>> data.drop_duplicates() v1 v2 0 a 1 1 a 2 4 a 3 5 b 4 7 b 5 8 b 3 #這兩個方法默認(rèn)會判斷全部列，你也可以指定部分列進(jìn)行重復(fù)項判斷。假設(shè)你還有一列值，且只希望根據(jù)v1列過濾重復(fù)項： >>> data['v3']=range(9) >>> data v1 v2 v3 0 a 1 0 1 a 2 1 2 a 2 2 3 a 2 3 4 a 3 4 5 b 4 5 6 b 4 6 7 b 5 7 8 b 3 8 >>> data.drop_duplicates(['v1']) v1 v2 v3 0 a 1 0 5 b 4 5 #duplicated和drop_duplicates默認(rèn)保留的是第一個出現(xiàn)的值組合。傳入take_last=True則保留最后一個： >>> data.drop_duplicates(['v1','v2'],take_last = True) v1 v2 v3 0 a 1 0 3 a 2 3 4 a 3 4 6 b 4 6 7 b 5 7 8 b 3 8

如果數(shù)據(jù)是列表格式的，有以下幾種方法可以刪除

list0=['b','c', 'd','b','c','a','a'] 方法1：使用set() list1=sorted(set(list0),key=list0.index) # sorted output print( list1) 方法2：使用 {}.fromkeys().keys() list2={}.fromkeys(list0).keys() print(list2) 方法3：set()+sort() list3=list(set(list0)) list3.sort(key=list0.index) print(list3) 方法4：迭代 list4=[] for i in list0: if not i in list4: list4.append(i) print(list4) 方法5：排序后比較相鄰2個元素的數(shù)據(jù)，重復(fù)的刪除 def sortlist(list0): list0.sort() last=list0[-1] for i in range(len(list0)-2,-1,-1): if list0[i]==last: list0.remove(list0[i]) else: last=list0[i] return list0 print(sortlist(list0))

五.噪音處理

噪音，是被測量變量的隨機誤差或方差。我們在上文中提到過異常點（離群點），那么離群點和噪音是不是一回事呢？我們知道，觀測量(Measurement) = 真實數(shù)據(jù)(True Data) + 噪聲 (Noise)。離群點(Outlier)屬于觀測量，既有可能是真實數(shù)據(jù)產(chǎn)生的，也有可能是噪聲帶來的，但是總的來說是和大部分觀測量之間有明顯不同的觀測值。。噪音包括錯誤值或偏離期望的孤立點值，但也不能說噪聲點包含離群點，雖然大部分?jǐn)?shù)據(jù)挖掘方法都將離群點視為噪聲或異常而丟棄。然而，在一些應(yīng)用（例如：欺詐檢測），會針對離群點做離群點分析或異常挖掘。而且有些點在局部是屬于離群點，但從全局看是正常的。

我在quora上看到過一個解釋噪音與離群點的有趣的例子：

Outlier: you are enumerating meticulously everything you have. You found 3 dimes, 1 quarter and wow a 100 USD bill you had put there last time you bought some booze and had totally forgot there. The 100 USD bill is an outlier, as it's not commonly expected in a pocket.

Noise: you have just come back from that club and are pretty much wasted. You try to find some money to buy something to sober up, but you have trouble reading the figures correctly on the coins. You found 3 dimes, 1 quarter and wow a 100 USD bill. But in fact, you have mistaken the quarter for a dime: this mistake introduces noise in the data you have access to.

To put it otherwise, data = true signal + noise. Outliers are part of the data.

翻譯過來就是：

離群點： 你正在從口袋的零錢包里面窮舉里面的錢，你發(fā)現(xiàn)了3個一角，1個五毛，和一張100元的毛爺爺向你微笑。這個100元就是個離群點，因為并不應(yīng)該常出現(xiàn)在口袋里..

噪聲： 你晚上去三里屯喝的酩酊大醉，很需要買點東西清醒清醒，這時候你開始翻口袋的零錢包，嘛，你發(fā)現(xiàn)了3個一角，1個五毛，和一張100元的毛爺爺向你微笑。但是你突然眼暈，把那三個一角看成了三個1元...這樣錯誤的判斷使得數(shù)據(jù)集中出現(xiàn)了噪聲

那么對于噪音我們應(yīng)該如何處理呢？有以下幾種方法：

1.分箱法

分箱方法通過考察數(shù)據(jù)的“近鄰”（即，周圍的值）來光滑有序數(shù)據(jù)值。這些有序的值被分布到一些“桶”或箱中。由于分箱方法考察近鄰的值，因此它進(jìn)行局部光滑。

用箱均值光滑：箱中每一個值被箱中的平均值替換。

用箱中位數(shù)平滑：箱中的每一個值被箱中的中位數(shù)替換。

用箱邊界平滑：箱中的最大和最小值同樣被視為邊界。箱中的每一個值被最近的邊界值替換。

一般而言，寬度越大，光滑效果越明顯。箱也可以是等寬的，其中每個箱值的區(qū)間范圍是個常量。分箱也可以作為一種離散化技術(shù)使用.

2. 回歸法

可以用一個函數(shù)擬合數(shù)據(jù)來光滑數(shù)據(jù)。線性回歸涉及找出擬合兩個屬性（或變量）的“最佳”直線，使得一個屬性能夠預(yù)測另一個。多線性回歸是線性回歸的擴展，它涉及多于兩個屬性，并且數(shù)據(jù)擬合到一個多維面。使用回歸，找出適合數(shù)據(jù)的數(shù)學(xué)方程式，能夠幫助消除噪聲。

六.一些實用的數(shù)據(jù)處理小工具

1.去掉文件中多余的空行

空行主要指的是（\n,\r,\r\n,\n\r等），在python中有個strip()的方法，該方法可以去掉字符串兩端多余的“空白”，此處的空白主要包括空格，制表符(\t)，換行符。不過親測以后發(fā)現(xiàn)，strip()可以匹配掉\n,\r\n,\n\r等，但是過濾不掉單獨的\r。為了萬無一失，我還是喜歡用麻煩的辦法，如下：

#-*- coding :utf-8 -*- #文本格式化處理，過濾掉空行 file = open('123.txt') i = 0 while 1: line = file.readline().strip() if not line: break i = i + 1 line1 = line.replace('\r','') f1 = open('filename.txt','a') f1.write(line1 + '\n') f1.close() print str(i)

2.如何判斷文件的編碼格式

#-*- coding:utf8 -*- #批量處理編碼格式轉(zhuǎn)換（優(yōu)化） import os import chardet path1 = 'E://2016txtutf/' def dirlist(path): filelist = os.listdir(path) for filename in filelist: filepath = os.path.join(path, filename) if os.path.isdir(filepath): dirlist(filepath) else: if filepath.endswith('.txt'): f = open(filepath) data = f.read() if chardet.detect(data)['encoding'] != 'utf-8': print filepath + "----"+ chardet.detect(data)['encoding'] dirlist(path1)

3.文件編碼格式轉(zhuǎn)換，gbk與utf-8之間的轉(zhuǎn)換

這個主要是在一些對文件編碼格式有特殊需求的時候，需要批量將gbk的轉(zhuǎn)utf-8的或者將utf-8編碼的文件轉(zhuǎn)成gbk編碼格式的。

#-*- coding:gbk -*- #批量處理編碼格式轉(zhuǎn)換 import codecs import os path1 = 'E://dir/' def ReadFile(filePath,encoding="utf-8"): with codecs.open(filePath,"r",encoding) as f: return f.read() def WriteFile(filePath,u,encoding="gbk"): with codecs.open(filePath,"w",encoding) as f: f.write(u) def UTF8_2_GBK(src,dst): content = ReadFile(src,encoding="utf-8") WriteFile(dst,content,encoding="gbk") def GBK_2_UTF8(src,dst): content = ReadFile(src,encoding="gbk") WriteFile(dst,content,encoding="utf-8") def dirlist(path): filelist = os.listdir(path) for filename in filelist: filepath = os.path.join(path, filename) if os.path.isdir(filepath): dirlist(filepath) else: if filepath.endswith('.txt'): print filepath #os.rename(filepath, filepath.replace('.txt','.doc')) try: UTF8_2_GBK(filepath,filepath) except Exception,ex: f = open('error.txt','a') f.write(filepath + '\n') f.close() dirlist(path1)

剛寫完比較粗糙，以后會不斷修改。下篇寫數(shù)據(jù)轉(zhuǎn)換方面的內(nèi)容，包括標(biāo)準(zhǔn)化，歸一化正則化等。如果有錯誤，歡迎指正！