幾乎所有的物理現象都可看作是信號,但這里我們特指動態振動信號。
振動信號采集與一般性模擬信號采集雖有共同之處,但存在的差異更多,因此,在采集振動信號時應注意以下幾點:
1、振動信號采集模式取決于機組當時的工作狀態,如穩態、瞬態等;
2、變轉速運行設備的振動信號采集在有條件時應采取同步整周期采集;
3、所有工作狀態下振動信號采集均應符合采樣定理。對信號預處理具有特定要求是振動信號本身的特性所致。信號預處理的功能在一定程度上說是影響后續信號分析的重要因素。
預處理方法的選擇也要注意以下條件:
1、在涉及相位計算或顯示時盡量不采用抗混濾波;
2、在計算頻譜時采用低通抗混濾波;
3、在處理瞬態過程中1X矢量、2X矢量的快速處理時采用矢量濾波。
上述第3條是保障瞬態過程符合采樣定理的基本條件。在瞬態振動信號采集時,機組轉速變化率較高,若依靠采集動態信號(一般需要若干周期)通過后處理獲得1X和2X矢量數據,除了效率低下以外,計算機(服務器)資源利用率也不高,且無法做到高分辨分析數據。機組瞬態特征(以波德圖、極坐標圖和三維頻譜圖等型式表示)是固有的,當組成這些圖譜的數據間隔過大(分辨率過低)時,除許多微小的變化無法表達出來,也會得出誤差很大的分析結論,影響故障診斷的準確度。一般來說,三維頻譜圖要求數據的組數(△rpm分辨率)較少,太多了反而影響對圖形的正確識別;但對前面兩種分析圖譜,則要求較高的分辨率。
目前公認的方式是每采集10組靜態數據采集1組動態數據,可很好地解決不同圖譜對數據分辨率的要求差異。影響振動信號采集精度的因素包括采集方式、采樣頻率、量化精度三個因素,采樣方式不同,采集信號的精度不同,其中以同步整周期采集為最佳方式;采樣頻率受制于信號最高頻率;量化精度取決于A/D轉換的位數,一般采用12位,部分系統采用16位甚至24位。振動信號的采樣過程,嚴格來說應包含幾個方面:
1、信號適調由于目前采用的數據采集系統是一種數字化系統,所采用的A/D芯片對信號輸入量程有嚴格限制,為了保證信號轉換具有較高的信噪比,信號進入A/D以前,均需進行信號適調。適調包括大信號的衰減處理和弱信號的放大處理,或者對一些直流信號進行偏置處理,使其滿足A/D輸入量程要求。2、A/D轉換A/D轉換包括采樣、量化和編碼三個組成部分。采樣(抽樣),是利用采樣脈沖序列p(t)從模擬信號x(t)中抽取一系列離散樣值,使之成為采樣信號x(n△t)(n=0,1,2,…)的過程。△t稱為采樣間隔,其倒數稱1/△t=fs之為采樣頻率。采樣頻率的選擇必須符合采樣定理要求。由于計算機對數據位數進行了規定,采樣信號x(n△t)經舍入的方法變為只有有限個有效數字的數,這個過程稱為量化。由于抽樣間隔長度是固定的(對當前數據來說),當采樣信號落入某一小間隔內,經舍入方法而變為有限值時,則產生量化誤差。如8位二進制為28=256,即量化增量為所測信號最大電壓幅值的1/256。編碼是把采樣數據轉變為計算機能識別的數字格式。一、采樣定理1、采樣定理
采樣定理解決的問題是確定合理的采樣間隔△t以及合理的采樣長度T,保障采樣所得的數字信號能真實地代表原來的連續信號x(t)。衡量采樣速度高低的指標稱為采樣頻率fs。一般來說,采樣頻率fs越高,采樣點越密,所獲得的數字信號越逼近原信號。為了兼顧計算機存儲量和計算工作量,一般保證信號不丟失或歪曲原信號信息就可以滿足實際需要了。這個基本要求就是所謂的采樣定理,是由Shannon提出的,也稱為Shannon采樣定理。Shannon采樣定理規定了帶限信號不丟失信息的最低采樣頻率為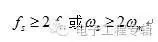
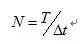
使用采樣頻率時有幾個問題需要注意。
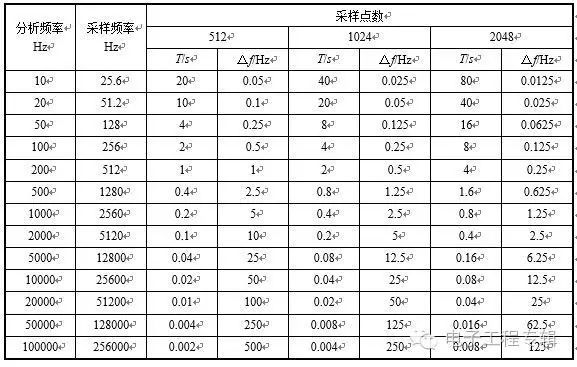
一,正確估計原信號中最高頻率成分的頻率,對于采用電渦流傳感器測振的系統來說,一般確定為最高分析頻率為12.5X,采樣模式為同步整周期采集,若選擇頻譜分辨率為400線,需采集1024點數據,若每周期采集32點,采樣長度為32周期。
二,同樣的數據量可以通過改變每周期采樣點數提高基頻分辨率,這對于識別次同步振動信號是必要的,但降低了最高分析頻率,如何確定視具體情況而定。
2、采樣定理解析
采樣定理實際上涉及了3個主要條件,當確定其中2個條件后,第3個條件自動形成。這3個條件是進行正確數據采集的基礎,必須理解深刻。條件1 采樣頻率控制最高分析頻率采樣頻率(采樣速率)越高,獲得的信號頻率響應越高,換言之,當需要高頻信號時,就需要提高采樣頻率,采樣頻率應符合采樣定理基本要求。這個條件看起來似乎很簡單,但對于一個未知信號,其中所含最高頻率信號的頻率究竟有多高,實際上我們是無法知道的。解決這個問題需要2個步驟,一是指定最高測量頻率,二是采用低通濾波器把高于設定最高測量頻率的成分全部去掉(這個低通濾波器就是抗混濾波器)。現實的抗混濾波器與理論上的濾波器存在差異,因此信號中仍會存在一定混疊成分,一般在計算頻譜后將高頻成分去掉,一般頻譜線數取時域數據點的1/2.56,或取頻域幅值數據點的1/1.28,即128線頻譜取100線,256線頻譜取200線,512線頻譜取400線等等。
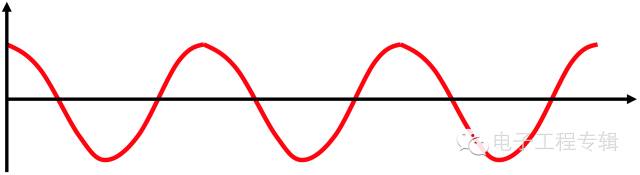
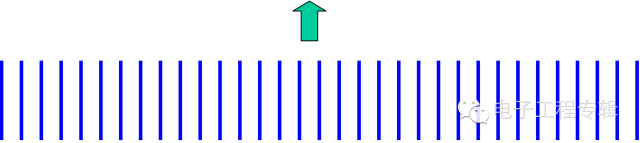
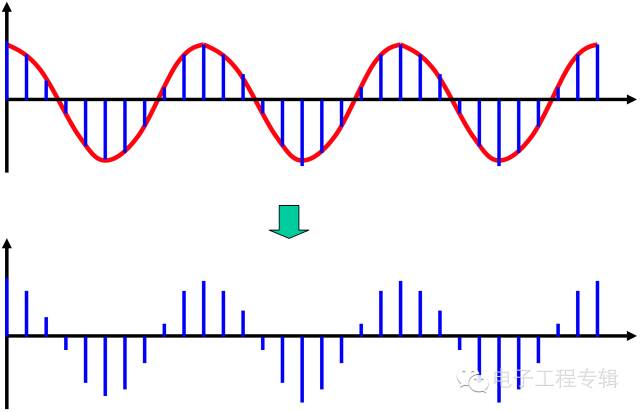
圖 、采樣過程示意圖抗混濾波器的使用主要是針對頻譜分析的,對于涉及相位計算的用途反而會引入相位誤差。幾乎所有的濾波器的相位特性遠比幅值特性差。為說明該條件,我們舉例進行說明。① 要想在頻譜中看到500Hz的成分,其采樣頻率最少為1000Hz。② 若采樣頻率為32點/轉,頻譜中最高線理論上可達到16X。
條件2 總采樣時間控制分辨率頻譜的分辨率(譜線間隔)受控于總采樣時間,即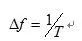
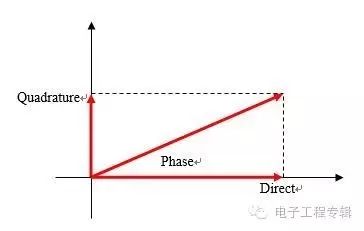
條件3 采樣點數控制頻譜線數解釋這個條件,需要對FFT計算頻譜的過程有一個了解。如果對于一個2048點的時間波形數據,我們可以獲得2048點頻域數據——1024線頻譜(每條譜線有兩個值,直接值和正交值,或者說幅值和相位兩個值)。對旋轉機械來說,頻譜僅僅畫出了FFT復數輸出的幅值部分,對于相位部分一般不畫,因此頻譜中的線數最多為時域點數的一半,考慮到混疊的影響,頻譜線數一般會低于時域數據點數。
小結采樣定理是實現正確采樣的基準,上述3個條件中,可以根據需要設置其中2個條件,第3個條件就會自動固定。① 如果采樣總時間為0.5秒,想獲得3200線頻譜,則有

4096下一個2的整數次冪的數值是8192,由此可獲得3200線的頻譜,其最高分析頻率達到了320Hz,可以滿足要求,可以通過提高采樣速率來實現這一要求。


【問題01】在不重采樣的前提下,能否提高頻譜的分辨率?
【問題02】對于旨在分析齒輪故障和滾動軸承故障的振動數據采集應注意什么事項?
理解了采樣定理的實質,我們就會對某些儀器/系統中列出的技術指標有了正確的認識,頻譜分辨率并不是衡量采樣質量的唯一指標,即400線頻譜與400線的頻譜之間有可能存在差異;在分析齒輪故障時就不會出現沒有嚙合頻率成分這樣的尷尬;在分析開/停車過程時出現分辨率過低問題……頻譜的功率泄漏問題數字信號分析需要選擇取合理的采樣長度,雖然在采樣過程中充分考慮了采樣定理和分析要求,但畢竟是一個用區間為(-T~T)的有限長度信號來近似t→∞信號的過程, |t|>T的x(t)值為零,因此所得到的頻譜和實際頻譜存在一定差異,這種現象稱之為泄漏現象。
影響數據采集過程的幾個關鍵環節
A/D轉換位數(轉換精度)
采樣方式(自由采集與整周期采集、同步自由采集與同步整周期采集)
數據采集的效率
數據采集中相位信號的作用
振動信號的預處理1、低通抗混濾波抗混濾波器是一種低通濾波器,如廣泛采用的8階橢圓濾波器。在線系統采樣單元中采用的抗混濾波器,應具備截至頻率可跟蹤性,即隨著機器轉速的變化,低通濾波器的截至頻率也隨之變化。
抗混濾波器的使用目的是避免頻譜分析時高頻分量折疊到低頻段,但每一種低通濾波器的相頻響應曲線并不像幅頻曲線那樣平坦。如某型號4階低通濾波器,在其截至頻率處相位偏移達-180°,在3kHz處偏移也有-45°,這個相位偏移足以影響幅值的正確計量。
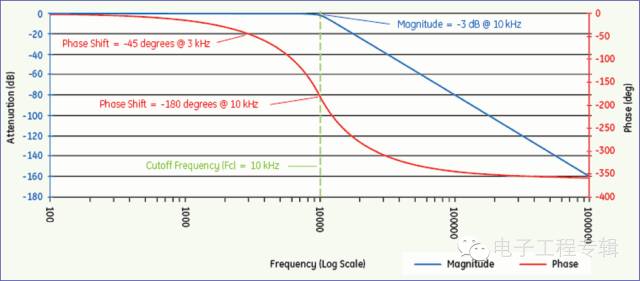
2、數字矢量濾波數字矢量濾波器是一種用特殊數字技術實現的跟蹤帶通濾波器,可實現1X、2X或設定分頻矢量值的功能。數字矢量濾波器在低速和高速下的帶寬設置不同,低速時帶寬設置窄一些,在高速時帶寬適當增大。通帶越窄,需要的響應時間越長,因此債的通帶只適用于低速段。如本特利公司的DVF3型數字矢量濾波器設置的帶寬及響應時間為:
表 、DVF3濾波參數設置表
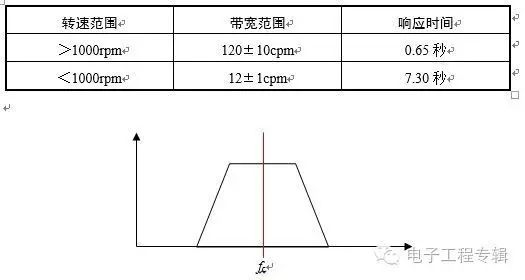
3、積分電路當采用殼體振動測量傳感器時,用戶可能需要使用某種特定的振動單位作為監測參量,以方便與相關標準對應。當采用加速度傳感器測量時,積分電路就是必要的預處理手段。
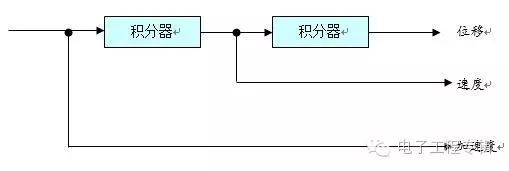
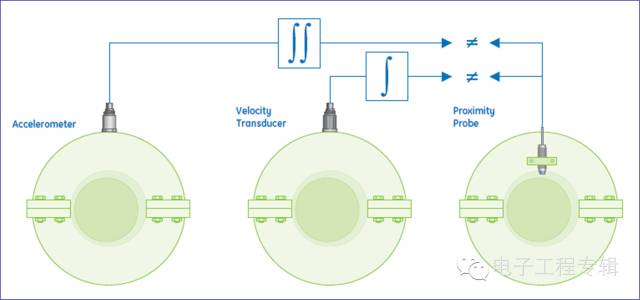
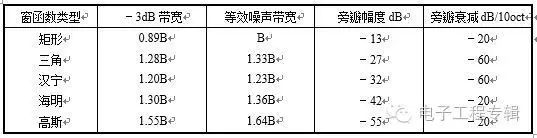
為了降低時間波形因截斷引起的頻域振蕩現象,在信號分析時多采用加窗的方式進行修正,窗函數就是截斷函數,不同的窗函數對旁瓣的抑制能力也有區別。一般來說,窗函數必須具備以下基本要求:窗譜的主瓣要窄且高,旁瓣要小,正負交替接近相等,以減小泄漏或負譜現象。
常用的窗函數及其性能指標如表所示。表 、典型窗函數的性能特點
5、其它問題與信號采集有關的問題還涉及到系統的輸入阻抗與輸入阻抗的問題。對于框架式儀表提供的緩沖輸出信號,其輸出阻抗多在幾百歐姆左右,如本特利公司的7200系列儀表和3300系列儀表的緩沖輸出阻抗為100歐姆,3500系列儀表的緩沖輸出阻抗為550歐姆。數據采集系統的輸入阻抗不易過低,理論上講輸入阻抗值越高越好。要保證信號損失率在1%以下,輸入輸出阻抗比應控制在100:1以上。信號損失率的定義為:
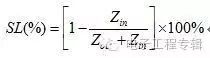
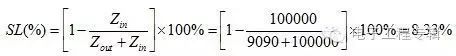
-
數據采集
+關注
關注
38文章
6055瀏覽量
113625 -
振動信號
+關注
關注
0文章
23瀏覽量
8847
原文標題:振動信號的采集與預處理
文章出處:【微信號:eet-china,微信公眾號:電子工程專輯】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 采集振動信號時應注意哪幾點?
采集振動信號時應注意哪幾點?












評論