圖像處理基本算法操作從處理對象的多少可以有如下劃分：

點運算：處理點單元信息的運算

群運算：處理群單元 （若干個相鄰點的集合）的運算

表1 圖像處理操作按處理對象數量分類表格

下圖是一副普通的吉普車圖像和我們生活中見到的并沒有什么兩樣，但是在計算機看來則是另外一副“模樣”了。圖像中黃色部分則是幾部車圖像倒車鏡的局部圖像在計算機中的形態。

圖1 計算機圖像的真實表現形態

以上圖為例說明幾種重要的點運算和群運算。

1. 二值化操作

圖像二值化是圖像處理中十分常見且重要的操作，它是將灰度圖像轉換為二值圖像或灰度圖像的過程。二值化操作有很多種，例如一般二值化、翻轉二值化、截斷二值化、置零二值化、置零翻轉二值化。

其中src(x,y)表示的是原始圖像中第x行第y列像素值。

如果去圖像中左上角3X3的鄰域，thresh取200，maxval取255，閾值方法選擇一般二值化（THRESH_BINARY），那么操作過后的結果如下：

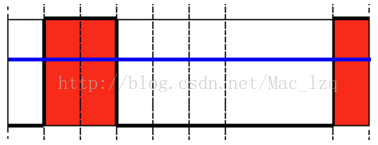
圖2 一般二值化圖示

在圖2中，一般二值化下底表示為0，上頂表示為maxval，其中藍色橫線則表示閾值（thresh）。超過該閾值則為maxval，否則為0。

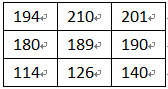
（a） 操作前

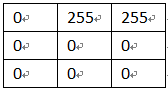
（b） 操作后

2. 直方圖處理

直方圖是圖像處理中另一重要處理過程，它反映圖像中不同像素值的統計信息。從這句話我們可以了解到直方圖信息僅反映灰度統計信息，與像素具體位置沒有關系。這一重要特性在許多識別類算法中直方圖處理起到關鍵作用。假設現有3X3的大小的圖像。像素值分別為6，3，3，8，6，8，3，3，3，那么它的統計直方圖則為

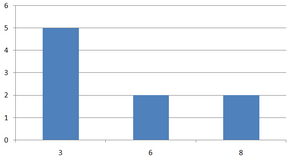
假設圖1中反光鏡的直方圖為下圖所示。

假設我們對直方圖中中某一灰度信息進行置零操作，那么反映在直方圖圖上則是該灰度的柱狀高度為0。

值得一說的是二值化處理和某些直方圖處理屬于不可逆運算，而亮度映射、加法運算、翻轉運算 、尺度運算 、對數運算 、指數運算等皆屬于可逆運算。

3. 模板卷積運算

模板運算是圖像處理中使用頻率相當高的一種運算，很多操作可以歸結為模板運算，例如平滑處理，濾波處理以及邊緣特征提取處理等。這里需要說明的是模板運算所使用的模板通常說來就是NXN的矩陣（N一般為奇數如3,5,7,...），如果這個矩陣是對稱矩陣那么這個模板也稱為卷積模板，如果不對稱則是一般的運算模板。我們通常使用的模板一般都是卷積模板。如邊緣提取中的Sobel算子模板。

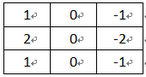
圖 4-a Mx算子模板

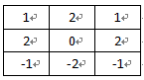
圖4-bMy算子模板

模板運算一般操作過程分為以下三個步驟：

定"錨點 "：就是處理之后的結果值的保存位置，該位置稱為"錨點 "，有時候也不在中心。

對位相乘：模板和原圖像的待處理區域，進行對位相乘運算

求和：將步驟2中模板區域內運算結果進行求和，將求和的結果置于"錨點 "

4. 形態學處理

形態學處理是二值圖像處理中的經典處理手段，主要有膨脹處理和腐蝕處理。也包含一些其他操作如 二值開閉運算、骨架抽取、極限腐蝕、擊中擊不中變換、形態學梯度、Top-hat變換、顆粒分析、流域變換等。

膨脹和腐蝕操作主要的功能有：

消除雜波，噪聲信息

填充圖像內部的"孔洞"

平滑邊緣毛刺

膨脹和腐蝕具有類似的數學模型，這里就一起介紹了，簡單來說膨脹就是取最大值，腐蝕操作是取最小值。

膨脹操作的數學表達式為：

腐蝕操作的數學表達式為：

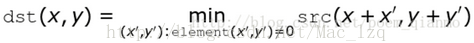
膨脹操作和腐蝕操作一般的處理過程如下：

按照選定的處理核(NxN，一般N為奇數)與源圖像的區域進行逐個“錨點”配對

將配對的處理鄰域信息進行相應操作，膨脹操作就取最大值，腐蝕操作就取最小值

求的結果作為源圖像中配對區域的數值。

圖a 原圖

圖b 膨脹處理圖

圖c 腐蝕處理